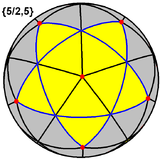
Малый звёздчатый додекаэдр

Малый звёздчатый додекаэдр
Тип	тело Кеплера — Пуансо
Звёздчатая форма	Правильного додекаэдра
Элементы	F = 12, E = 30, V = 12
Характеристика Эйлера	${\displaystyle \chi }$= -6
Грани по типам	12{5/2}
Символ Шлефли	{5/2,5}
Символ Витхоффа	5 | 25/2
Диаграмма Коксетера
Группа симметрии	Ih, H3, [5,3], (*532)
Обозначения	U34,C43, W20
Свойства	правильный невыпуклый
(5/2)5 (Вершинная фигура)	Большой додекаэдр (двойственный многогранник)

Малый звёздчатый додекаэдр^[1][2][3] — тело Кеплера — Пуансо, с символом Шлефли {5/2,5}. Многограннику дал имя Артур Кэли. Многогранник является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 граней в виде пентаграмм с пятью пентаграммами, сходящимися в каждой вершине.

Он имеет то же самое расположение вершин^[англ.], что и выпуклый правильный икосаэдр. Кроме того, у него то же самое расположение рёбер^[англ.], что и у большого икосаэдра.

Он считается первой звёздчатой формой додекаэдра.

Если рассматривать грани в виде пентаграммы как 5 отдельных треугольных граней, он имеет ту же топологию поверхности, что и пентакисдодекаэдр, но с существенно более острыми равнобедренными треугольными гранями с такой высотой пятиугольных пирамид, что пять треугольников становятся копланарными (лежащими в одной плоскости).

Прозрачная модель	Собранные вручную модели
(см. также : в движении)
Сферическая мозаика	Звёздчатая форма	Развёртка
Этот многогранник представляет также сферическую мозаику с плотностью 3. (Одна сферическая грань в виде пентаграммы прочерчена синей линией и заполнена жёлтым)	Его можно построить как первую из трёх звёздчатых форм додекаэдра и его номер в списке моделей Веннинджера [W20].	× 12 Малый звёздчатый додекаэдр можно построить из бумаги или картона путём соединения двенадцати пятиугольных равнобочных пирамид таким же образом, как располагаются пятиугольники в правильном додекаэдре.

• Его также можно видеть в мозаике пола в соборе Святого Марка в Венеции, автор Паоло Уччелло, около 1430.
• Он является центральной фигурой в двух литографиях Эшера — Контраст (Порядок и хаос) (1950) и Гравитация (1952).

Выпуклая оболочка многогранника является икосаэдром. Он также имеет общие рёбра с большим икосаэдром.

Этот многогранник является усечением большого додекаэдра — усечённый малый звёздчатый додекаэдр выглядит как додекаэдр, но имеет не 12, а 24 грани — 12 пятиугольников, полученных от усечения вершин, и 12 перекрывающих их пятиугольников (полученных от усечения пентаграм).

Название	Малый звёздчатый додекаэдр	Усечённый малый звёздчатый додекаэдр	Додекододекаэдр	Усечённый большой додекаэдр[англ.]	Большой додекаэдр
Диаграмма Коксетера
Рисунок

• Соединение малого звёздчатого додекаэдра и большого додекаэдра^[англ.]

• Eric W. Weisstein^[англ.] Small Stellated Dodecahedron (Uniform polyhedron) на MathWorld
  • Weisstein, Eric W. DodecahedronStellations (англ.) на сайте Wolfram MathWorld.
• Uniform polyhedra and duals
• Bronze sculpture of small stellated dodecahedron

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии. После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.