|
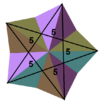
Большой додекаэдр
Большой додекаэдр[1][2][3] — это тело Кеплера — Пуансо с символом Шлефли {5,5/2} и диаграммой Коксетера — Дынкина Изображения
Связанные многогранникиМногогранник имеет то же самое расположение рёбер[англ.], что и выпуклый правильный икосаэдр. Если большой додекаэдр рассматривать как многогранник, имеющий нормальные треугольные грани (обычно гранью большого додекаэдра считается плоский пятиугольник, часть которого находится внутри), то он имеет ту же топологию, что и триакисикосаэдр (поверхность рода 4), но с вогнутыми пирамидами, а не выпуклыми. Процесс усечения, применённый к большому додекаэдру даёт серию невыпуклых однородных многогранников. Усечение рёбер до их полного уничтожения (превращения в точку) даёт додекододекаэдр. Применение процесса полного усечения граней (до превращения в точку) даёт малый звёздчатый додекаэдр.
Использование
См. такжеПримечания
Литература
Ссылки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||