Espai bidimensional

L'espai bidimensional és una configuració geomètrica en la qual es requereixen dos valors (anomenats paràmetres) per determinar la posició d'un element (d'un punt).^[1][2] En matemàtiques se sol representar pel símbol ℝ². Per una generalització del concepte, vegeu Dimensió.

L'espai bidimensional es pot veure com una projecció de l'univers físic sobre un pla. Normalment se'l considera com un espai euclidià i les dues dimensions s'anomenen ample i llarg (no té profunditat).^[3][4]

Els llibres I-IV i VI dels Elements d'Euclides versen sobre la geometria bidimensional, desenvolupant nocions com la similitud de formes, el teorema de Pitàgores (Proposició 47), la igualtat dels angles i les àrees, el paral·lelisme, la suma dels angles en un triangle i els tres casos en què els triangles són "iguals" (tenen la mateixa àrea), entre molts altres temes.

Posteriorment, el pla es va descriure en un sistema de coordenades anomenat cartesià, un sistema de coordenades que especifica cada punt de forma única en un pla a partir d'un parell de coordenades numèriques, que són les distàncies entre el punt i dues línies perpendiculars fixes, mesurades en la mateixa unitat de mesura. Cada línia de referència rep el nom d'eix de coordenades o simplement eix del sistema, i el punt on es troben és l'origen. Les coordenades també es poden definir com les posicions de les projeccions perpendiculars del punt sobre els dos eixos, expressades com distàncies amb signe des de l'origen.

La idea d'aquest sistema va ser desenvolupada l'any 1637 en escrits de Descartes i independientment per Pierre de Fermat, tot i que Fermat també va treballar en tres dimensions, i no va publicar el seu descobriment.^[5] Tots dos autors van utilitzar un sol eix en els seus tractaments i tenen una longitud variable mesurada en referència a aquest eix. El concepte d'utilitzar un parell d'eixos es va introduir més tard, després que La Géométrie^[6] de Descartes fos traduïda al llatí l'any 1649 per Frans van Schooten i els seus alumnes.^[7] Aquests comentaristes van introduir diversos conceptes en intentar esclarir les idees contingudes en l'obra de Descartes.^[8]

Més tard, es va pensar en el pla com un cos, en què dos punts qualssevol es poden multiplicar i, excepte el 0, dividir-se. Això es coneixia com el pla complex. El pla complex de vegades es denomina pla d'Argand ja que s'utilitza en els diagrames d'Argand. Aquests duen el nom de Jean-Robert Argand (1768-1822), tot i que van ser descrits per primer cop per l'agrimensor i matemàtic danès-noruec Caspar Wessel (1745-1818).^[9] Els diagrames d'Argand s'utilitzen sovint per traçar les posicions dels pols i zeros d'una funció en el pla complex.

En matemàtiques, un pla euclidià és un espai euclidià de dimensió dos, denotat com E². Es tracta d'un espai geomètric en què calen dos nombres reals per determinar la posició de cada punt. És un espai afí, que inclou en particular el concepte de rectes paral·leles. També té propietats mètriques induïdes per la distància, que permet definir els cercles, i els angles.

Un pla euclidià juntament amb un sistema de coordenades cartesianes s'anomena pla cartesià. El conjunt ${\displaystyle \mathbb {R} ^{2}}$ de parelles de nombres reals (l'espai coordenat real), equipat amb un producte escalar, s'anomena sovint el pla euclidià, ja que tot pla euclidià n'és un isomorfisme.

En geometria euclidiana, un pla és una superfície plana bidimensional que s'estén indefinidament. Els plans euclidians solen aparèixer com a subespais de l'espai tridimensional ${\displaystyle \mathbb {R} ^{3}}$. Un exemple prototípic és el de les parets d'una habitació, esteses infinitament i assumides infinitament planes. Així com només cal un parell de nombres reals ${\displaystyle \mathbb {R} ^{2}}$ per descriure un punt en un pla, la relació amb punts de fora del pla requereix tenir en consideració el seu embedding en l'espai ambient ${\displaystyle \mathbb {R} ^{3}}$.

El pla el·líptic és el pla projectiu real equipat amb una mètrica. Kepler i Desargues van utilitzar la projecció gnomònica per relacionar un pla σ amb punts en un hemisferi tangent a ell. Sent O el centre de l'hemisferi, un punt P en σ determina una línia OP que intersecta l'hemisferi, i tota línia L ⊂ σ determina un pla OL que intersecta l'hemisferi en la meitat d'un gran cercle. L'hemisferi és fitat per un pla a través de O i paral·lel a σ. No hi ha cap línia ordinària de σ que correspongui a aquest pla; enlloc d'això una recta en l'infinit és annexada a σ. Com que tota línia en aquesta extensió de σ correspon a un pla a través de O, i com que tota parlela de tals plans intersecta en una línia a través de O, es pot concloure que tota parella de línies en l'extensió es tallen: el punt d'intersecció es troba on el pla d'intersecció es troba amb σ o amb la recta en l'infinit. Així doncs, l'axioma de la geometria projectiva, que implica que totes les parelles de rectes en un pla es tallen, es confirma.^[10]

Donats dos punts P i Q a σ, la distància el·líptica entre ells és la mesura de l'angle POQ, normalment donada en radians. Arthur Cayley va iniciar l'estudi de la geometria el·líptica, en la seva obra "On the definition of distance" ("Sobre la definició de la distància").^[11]:82 El van seguir en aquest viatge en l'abstracció de la geometria Felix Klein i Bernhard Riemann que van introduir la geometria no euclidiana i la geometria riemanniana.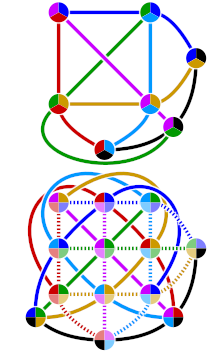

En matemàtiques, un pla projectiu és una estructura geomètrica que estén el concepte de pla. En el pla euclidià ordinari, dues línies se solen tallar en un únic punt, però hi ha una classe de rectes (les anomanades rectes parel·leles) que no es tallen. Un pla projectiu es pot pensar com un pla ordinari proveït amb "punts addicionals a l'infinit" on les rectes paral·leles es tallen. Així doncs, dues rectes diferents qualssevol en el pla projectiu es tallen en exactament un punt.

Els artistes del Renaixement, quan van desenvolupar les tècniques de dibuix amb perspectiva, van introduir aquest tema matemàtic. L'exemple arquetípic d'això és el pla projectiu real, també conegut com pla euclidià estès.^[12] Aquest exemple, en termes lleugerament diferents, és important en la geometria algebraica, la topologia i en la geometria projectiva en què es pot denotar com PG(2, R), RP², o P₂(R), d'entre d'altres notacions. Hi ha molts altres plans projectius, tant d'inifinits, com és el cas del pla projectiu complex, com de finits, com el pla de Fano.

Un pla projectiu és un espai projectiu de 2 dimensions, però no tots els plans projectius es poden incrustar en espais projectius tridimensionals. Tal incrustabilitat és una conseqüència d'una propietat coneguda com el teorema de Desargues, que no és compartida per tots els plans projectius.

A més de la seva estructura geomètrica familiar, amb isomorfismes que són isometries respecte el producte escalar habitual, es pot veure el pla des de diferents nivells d'abstracció. Cada nivell d'abstracció correspon a una categoria específica.

En un extrem, tots els conceptes geomètrics i mètrics es poden deixar de banda en el que es coneix com a pla topològic, que es pot entendre com una làmina infinita i idealitzada homotòpicament trivial, que manté la noció de proximitat, però en què no hi ha distàncies. El pla topològic té el concepte de camí lineal, però no el concepte de línia recta. El pla topològic, o el seu equivalent el disc obert, és el veïnat topològic bàsic que s'utilitza per construir superfícies (o 2-varietats) classificades en la topologia de poques dimensions. Els isomorfismes del pla topològic són totes bijeccions contínues. El pla topològic és el context natural per la branca de la teoria de grafs que treballa amb objectes com els grafs plans, i que té resultats com el teorema dels quatre colors.

També es pot veure el pla com un espai afí, els isomorfismes del qual són combinacions de translacions i aplicacions lineals no singulars. Des d'aquest punt de vista, no hi ha distàncies, sinó colinearitat i es preserven els ràtios de distàncies en tota recta.

La geometria diferencial veu el pla com una varietat bidimensional, un pla topològic que està equipat amb una estructura diferencial. També en aquest cas, no existeix la noció de distància, però sí que hi ha un concepte de continuïtat de funcions, per exemple un camí pot ser diferenciable o suau (en funció del tipus d'estructura diferenciable aplicat). Els isomorfismes en aquest cas són bijeccions amb el nivell de diferenciabilitat que sigui.

En la direcció oposada de l'abstracció, es pot aplicar una estructura de cos compatible al pla geomètric, donant lloc al pla complex i el camp de l'anàlisi complexa. El cos complex té només dos isomorfismes que mantenen fixa la recta real, la identitat i la conjugació.

Igual que en el cas real, el pla també pot ser vist com la varietat complexa més simple d'una dimensió (sobre els nombres complexos), alguna vegada anomenada recta complexa. Tanmateix, aquest punt de vista contrasta fortament amb el cas del pla com a varietat real de dues dimensions. Tots els isomorfimes són bijeccions conformes del pla complex, però les úniques possibilitats són aplicacions que corresponen a la composició d'una multiplicació amb un nombre complex i una translació.

A més, la geometria euclidiana (que té curvatura zero pertot) no és l'única geometria que pot tenir un pla. Al pla se li pot donar geometria esfèrica utilitzant la projecció estereogràfica. Això es pot entendre com si se situés una esfera tangent al pla (com una pilota al terra), traient el punt de dalt, i projectant l'esfera en el pla des d'aquest punt. Aquesta és només una de les projeccions que es poden utilitzar per fer un mapa pla d'una part de la superfície de la Terra. La geometria resultant té una curvatura positiva i constant.

Alternativament, al pla també se li pot donar una mètrica que li fa tenir curvatura constant negativa, en el que es coneix com el pla hiperbòlic. Aquesta possibilitat té aplicacions en la teoria de la relativitat especial en el cas simplificat en què hi ha dues dimensions espacials i una de temporal. (El pla hiperbòlic és una hipersuperfície en l'espaitemps en l'espai de Minkowski tridimensional.)

Una altra forma de veure un espai bidimensional és mitjançant l'àlgebra lineal, en què la idea d'independència és crucial. El pla té dues dimensions perquè la longitud del rectangle és independent de la seva amplada. En el llenguatge tècnic de l'àlgebra lineal, el pla és bidimensional perquè cada punt pot ser descrit per una combinació lineal de dos vectors independents.

Es defineix el producte escalar de dos vectors A = [A₁, A₂] i B = [B₁, B₂] com^[13]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}}$

Un vector pot ser pensat com una fletxa. La seva magnitud és la longitud i la seva direcció és la direcció en què apunta la fletxa. S'expressa la magnitud o mòdul d'un vector A com${\displaystyle \|\mathbf {A} \|}$. En aquesta forma, es defineix el producte escalar de dos vectors euclidians A i B com^[14]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,}$

on θ és l'angle entre A y B.

El producte escalar d'un vector A per ell mateix és

${\displaystyle \mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2},}$

que dona com a resultat

${\displaystyle \|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }},}$

la fórmula per a la longitud euclidiana del vector.

En la teoria de grafs, un graf pla és un graf que es pot incrustar en el plano, és a dir, que es pot dibuixar en un pla de tal manera que el seus enllaços es tallin només en els vèrtexs. En altres paraules, es pot dibuixar de tal manera que els seus enllaços no creuin entre sí.^[15] Un graf pla es pot encabir en el pla assignant a cada vèrtex un punt en el pla i relacionant cada enllaç amb una corba del pla, talment que els puns finals de cada corba són punts assignats des dels seus punts finals i totes le corbe són disjuntes (no tenen cap punt en comú) excepte en els seus punts extrems, els vèrtexs.

• Computació gràfica 2D
• Espai tridimensional