|
Claudi Ptolemeu
Claudi Ptolemeu (en grec antic: Κλαύδιος Πτολεμαίος, Klaudios Ptolemaios); ca. 85 - ca. 165, altres autors diuen ca. 100- ca. 170) va ser un astrònom, geògraf i matemàtic grecoegipci, anomenat comunament Ptolemeu o Tolemeu. BiografiaVa viure i treballar a Alexandria, Egipte (hom creu que a la famosa Biblioteca d'Alexandria). Va ser astròleg i astrònom, activitats que en eixa època estaven íntimament lligades. És autor del tractat astronòmic conegut com a Almagest (en grec Hè Megalè Syntaxis, El gran tractat). Es va preservar, com tots els tractats grecs clàssics de ciència, en manuscrits àrabs (d'ací el seu nom) i només disponible en llatí en la traducció de Gerard de Cremona en el segle xii. Hereu de la concepció de l'univers donada per Plató i Aristòtil, el seu mètode de treball va diferir notablement del d'aquestos, perquè mentre Plató i Aristòtil donen una cosmovisió de l'univers, Ptolemeu és un empirista. El seu treball va consistir a estudiar la gran quantitat de dades existents sobre el moviment dels planetes a fi de construir un model geomètric que explicara aquestes posicions en el passat i fóra capaç de predir les seves posicions futures. La ciència grega tenia dues possibilitats en el seu intent d'explicar la natura: l'explicació realista, que consistiria a expressar de manera rigorosa i racional el que realment es dona en la natura; i l'explicació positivista, que consistiria a expressar de manera racional l'aparent, sense preocupar-se de la relació entre el que es veu i el que en realitat és. Ptolemeu afirma explícitament que el seu sistema no pretén descobrir la realitat, perquè és només un mètode de càlcul. És lògic que adoptara un esquema positivista, perquè la seva teoria geocèntrica s'oposa flagrantment a la física aristotèlica: per exemple, les òrbites del seu sistema són excèntriques, en contraposició a les circulars i perfectes de Plató i Aristòtil. Ptolemeu va catalogar molts estels, assignant-los una brillantor i magnitud, i va establir normes per a predir els eclipsis.  La seva aportació fonamental va ser el seu model de l'univers: creia que la Terra era esfèrica i estava immòbil i ocupava el centre de l'univers, i que el Sol, la Lluna, els planetes i les estrelles, giraven al seu voltant.[1] Malgrat això, per mitjà de la tècnica de l'epicicle-deferent, la invenció del qual s'atribuïx a Apol·loni de Perge, tracta de resoldre amb prou d'èxit els dos grans problemes del moviment planetari:
Les seves teories astronòmiques van influir en el pensament astrònom i matemàtic científic fins al segle xvi. Ptolemeu aplicà els seus estudis de trigonometria a la construcció d'astrolabis i rellotges de sol. I també va aplicar l'estudi de l'astronomia al de l'astrologia, creant els horòscops. Totes estes teories i estudis estan escrits en la seua obra Tetrabiblon.  També va ser un bon òptic i geògraf. En el camp de l'òptica, va explorar les propietats de la llum, sobretot de la refracció i la reflexió. La seva obra Òptica és un bon tractat sobre la teoria matemàtica de les propietats de la llum. Una altra gran obra seva és la Geografia, que descriu el món de la seva època, amb mapes d'Agatòdemon. Hi utilitzà un sistema de latitud i longitud, que després va servir d'exemple als cartògrafs durant molts anys. Una de les ciutats descrita en esta obra és la Meca, a la península Aràbiga, a la qual anomena Makoraba. El món de la música tampoc no va ser ignorat per Ptolemeu. Va escriure un tractat de teoria musical anomenat Harmònics. AstronomiaL'astronomia fou el tema al qual Ptolemeu dedicà més temps i esforç; aproximadament la meitat de totes les obres que sobrevisqueren tracten de temes astronòmics, i fins i tot d'altres com la Geografia i els Tetrabiblos tenen referències significatives a l'astronomia.[2] Sintaxi matemàtica Syntaxis Mathēmatikē de Ptolemeu (grec antic: Μαθηματικὴ Σύνταξις, literalment «Tractat de matemàtica sistemàtic»), més conegut com l'Almagest, és l'únic tractat antic complet que es conserva sobre astronomia. Encara que els astrònoms babilònics havien desenvolupat tècniques aritmètiques per calcular i predir fenòmens astronòmics, aquestes no es basaven en cap model subjacent del cel. Els primers astrònoms grecs, d'altra banda, proporcionaren models geomètrics qualitatius per «salvar les aparences» dels fenòmens celestes sense la capacitat de fer cap predicció.[3] La persona més antiga que intentà fusionar aquests dos enfocaments fou Hiparc, que produí models geomètrics que no només reflectien la disposició dels planetes i les estrelles, sinó que es podien utilitzar per calcular els moviments celestes.[4] Ptolemeu, en la línia d'Hiparc, derivà cadascun dels seus models geomètrics per al Sol, la Lluna i els planetes a partir d'observacions astronòmiques seleccionades fetes durant més de vuit-cents anys; tanmateix, molts astrònoms han sospitat durant segles que alguns dels paràmetres dels seus models s'adoptà independentment de les observacions.[5] Ptolemeu presentà els seus models astronòmics juntament amb taules convenients, que es podrien utilitzar per calcular la posició futura o passada dels planetes.[6] L'Almagest també conté un catàleg d'estrelles, que és una versió d'un catàleg creat per Hiparc. La seva llista de quaranta-vuit constel·lacions és ancestral del sistema modern de constel·lacions, però, a diferència del sistema modern, no cobrien tot el cel (només el que es podia veure a ull nu).[7] Durant més de mil anys, l'Almagest fou el text autoritzat sobre astronomia a Europa, Orient Mitjà i el nord d'Àfrica, i el seu autor aviat es convertí en una figura gairebé llegendària: Ptolemeu, rei d'Alexandria.[8] L'Almagest es conservà, com moltes obres científiques gregues existents, en manuscrits àrabs. Es creu que el títol modern és una corrupció àrab del nom grec Hē Megistē Syntaxis (literalment «El tractat més gran»), com es creu que es coneixia l'obra a l'Antiguitat tardana.[9] A causa de la seva reputació, va ser àmpliament cercat i traduït dues vegades al llatí al segle xii, una a Sicília i una altra a la península Ibèrica.[10] Els models planetaris de Ptolemeu, com els de la majoria dels seus predecessors, foren geocèntrics i gairebé universalment acceptats fins a la reaparició dels models heliocèntrics durant la revolució científica. Taules pràctiquesLes Taules pràctiques (grec antic: Πρόχειροι κανόνες) són un conjunt de taules astronòmiques, juntament amb cànons per al seu ús. Per facilitar els càlculs astronòmics, Ptolemeu va tabular totes les dades necessàries per calcular les posicions del Sol, la Lluna i els planetes, la sortida i la posta de les estrelles i els eclipsis de Sol i de Lluna, convertint-lo en una eina útil per als astrònoms i astròlegs. Les taules en si es coneixen a través de la versió de Teó d'Alexandria. Encara que les Taules pràctiques de Ptolemeu no sobreviuen com a tals en àrab o en llatí, representen el prototip de la majoria de taules astronòmiques o zijs àrabs i llatines.[11] A més, la introducció a les Taules pràctiques sobrevisqué per separat de les mateixes taules (aparentment forma part d'una compilació d'alguns dels escrits més breus de Ptolemeu) sota el títol Arranjament i càlcul de les taules útils.[12] Hipòtesis planetàries Les Hipòtesis planetàries (grec antic: Ὑποθέσεις τῶν πλανωμένων) és una obra cosmològica, probablement una de les darreres escrites per Ptolemeu, en dos llibres que tracten sobre l'estructura de l'univers i les lleis que regeixen el moviment celeste.[13] Ptolemeu va més enllà dels models matemàtics de l'Almagest per presentar una realització física de l'univers com un conjunt d'esferes imbricades,[14] en les quals utilitzà els epicicles del seu model planetari per calcular les dimensions de l'univers. Estimà que el Sol es trobava a una distància mitjana de 1.210 radis terrestres (ara se sap que en realitat són ~23.450 radis), mentre que el radi de l'esfera de les estrelles fixes era 20.000 vegades el radi de la Terra.[15] L'obra també destaca per tenir descripcions sobre com construir instruments per representar els planetes i els seus moviments des d'una perspectiva geocèntrica, com un planetari mecànic heliocèntric, presumiblement amb finalitats didàctiques.[16] Altres obresL'Analemma és un breu tractat on Ptolemeu proporciona un mètode per especificar la ubicació del sol en tres parells d'arcs de coordenades orientats localment en funció de la declinació del sol, la latitud terrestre i l'hora. La clau de l'enfocament és representar la configuració sòlida en un diagrama pla que Ptolemeu anomena analema.[17] En una altra obra, la Phaseis (Ascens de les estrelles fixes), Ptolemeu oferí un parapegma, un calendari estel·lar o almanac, basat en les aparicions i desaparicions d'estrelles al llarg de l'any solar.[18] El Planisphaerium (en grec antic: Ἅπλωσις ἐπιφανείας σφαίρας, literalment «Simplificació de l'esfera») conté 16 proposicions que tracten la projecció dels cercles celestes sobre un pla. El text es perd en grec (excepte un fragment) i perviu només en àrab i llatí.[19] Ptolemeu també va erigir una inscripció en un temple de Canop, al voltant del 146–147 dC, coneguda com la Inscripció Canòbica. Tot i que la inscripció no ha sobreviscut, algú al segle vi la transcrigué i les còpies manuscrites la conservaren durant l'edat mitjana. Comença: «Al déu salvador, Claudi Ptolemeu [dedica] els primers principis i models de l'astronomia», seguint un catàleg de números que defineixen un sistema de mecànica celeste que regeix els moviments del sol, la lluna, els planetes i les estrelles.[20] Cartografia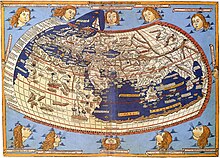 La segona obra més coneguda de Ptolemeu és la seva Geographike Hyphegesis (en grec antic: Γεωγραφικὴ Ὑφήγησις; literalment «Guia per dibuixar la Terra»), conegut com a Geografia, un manual sobre com dibuixar mapes utilitzant coordenades geogràfiques de parts del món romà conegudes en aquell moment.[21][22] Es basà en treballs anteriors del geògraf Marí de Tir, així com en els registres de l'Imperi romà i antic persa.[22][23] També reconegué la tasca l'antic astrònom Hiparc per haver calculat l'elevació del pol nord celeste[24] per a algunes ciutats. Encara que els mapesbasats en principis científics s'havien fet des de l'època d'Eratòstenes (c. 276–195 aC), Ptolemeu millorà les projeccions cartogràfiques. La primera part de la Geografia és una discussió de les dades i dels mètodes que utilitzà. Ptolemeu assenyala la supremacia de les dades astronòmiques sobre les mesures terrestres o els informes dels viatgers, tot i que posseïa aquestes dades només per pocs llocs. La veritable innovació de Ptolemeu, però, es produeix a la segona part del llibre, on ofereix un catàleg de 8.000 localitats que recollí de Marí i d'altres, la base de dades més gran de l'antiguitat.[25] Uns 6.300 d'aquests llocs i característiques geogràfiques tenen coordenades assignades perquè es puguin col·locar en una quadrículaque abasta tot el món.[2] La latitud es mesurava des de l'equador, com avui, però Ptolemeu preferí dir-ne clima, la durada del dia més llarg en lloc de graus d'arc: la durada del dia de mitjan estiu augmenta de dotze a vint-i-quatre hores a mesura que es va des de l'equador al cercle polar.[26] Un dels llocs on Ptolemeu assenyalà coordenades específiques fou l'ara perduda Torre de Pedra que marcava el punt mitjà de l'antiga Ruta de la Seda, i que els estudiosos han intentat localitzar des de llavors.[27] A la tercera part de la Geografia, Ptolemeu dona instruccions sobre com crear mapes tant de tot el món habitat (oikoumenē) com de les províncies romanes, incloses les llistes topogràfiques necessàries, i les llegendes dels mapes. El seu oikoumenē abastava 180 graus de longitud des de les Illes Afortunades de l'oceà Atlàntic fins al centre de la Xina, i uns 80 graus de latitud des de les Shetland fins a anti-Meroe (costa est d'Àfrica); Ptolemeu era molt conscient que només coneixia una quarta part del món, i una extensió errònia de la Xina cap al sud suggereix que les seves fonts no arribaren fins a l'oceà Pacífic.[23][22] Sembla probable que les taules topogràfiques de la segona part de l'obra (llibres 2-7) siguin textos acumulatius, que es modificaren a mesura que es disposaren de nous coneixements en els segles posteriors a Ptolemeu.[28] Això vol dir que la informació continguda en diferents parts de la Geografia és probable que sigui de dates diferents, a més de contenir molts errors d'escriptura. Tanmateix, encara que els mapes regionals i mundials dels manuscrits supervivents daten del ca. 1300 dC (després que el text fos redescobert per Planudes Màxim), hi ha alguns estudiosos que pensen que aquests mapes es remunten al mateix Ptolemeu.[25] Astrologia Ptolemeu escrigué un tractat astrològic, en quatre parts, conegut amb el terme grec Tetrabiblos (literalment «Quatre llibres») o pel seu equivalent llatí Quadripartitum.[29] Se'n desconeix el títol original, però pot haver estat un terme que es troba en alguns manuscrits grecs, Apotelesmatiká (biblía), que significa aproximadament «(llibres) sobre els efectes» o «Resultats», o «Pronòstic».[30] Com a font de referència, es diu que els Tetrabiblos «va gaudir gairebé de l'autoritat d'una Bíblia entre els escriptors astrològics durant mil anys o més».[31] Va ser traduït per primera vegada de l'àrab al llatí per Plató de Tívoli (Tiburtinus) l'any 1138, mentre era a Hispània.[32] Gran part del contingut dels Tetrabiblos fou recollit de fonts anteriors. L'èxit de Ptolemeu fou ordenar el seu material d'una manera sistemàtica, mostrant com es podia, segons ell, racionalitzar el tema. Es presenta, de fet, com la segona part de l'estudi de l'astronomia de la qual l'Almagest fou la primera, relacionada amb les influències dels cossos celestes a l'esfera sublunar.[33][34] Així, es proporcionen una mena d'explicacions sobre els efectes astrològics dels planetes, basant-se en els seus efectes combinats d'escalfament, refredament, humectació i assecament.[35] Ptolemeu descarta altres pràctiques astrològiques, com ara considerar la importància numerològica dels noms, que creia que no tenien una base sòlida, i deixa de banda temes populars, com ara l'astrologia electoral i l'astrologia mèdica, per motius semblants.[36] La gran popularitat que tenien els Tetrabiblos es podria atribuir a la seva naturalesa com a exposició de l'art de l'astrologia i com a compendi de coneixements astrològics, més que com a manual. Parla en termes generals, evitant il·lustracions i detalls de la pràctica. Una col·lecció de cent aforismes sobre astrologia anomenada Centiloquium, atribuïda a Ptolemeu, va ser àmpliament reproduïda i comentada per erudits àrabs, llatins i hebreus, i sovint lligades en manuscrits medievals després dels Tetrabiblos com una mena d'afegit.[2] Ara es creu que és una composició pseudoepigràfica molt posterior. La identitat i la data de l'autor real de l'obra, denominat ara Pseudo-Ptolemeu, segueix sent objecte de conjectures.[37] Música Ptolemeu escrigué Harmonikon (en grec antic: Ἁρμονικόν), conegut com els Harmònics, sobre teoria de la música i les matemàtiques darrere de les escales musicals.[38] Comença amb una definició de la teoria harmònica, amb una llarga exposició sobre la relació entre la raó i la percepció dels sentits en la corroboració de supòsits teòrics. Després de criticar els plantejaments dels seus predecessors, Ptolemeu defensa que es basin els intervals musicals en ràtios matemàtics (en contrast amb els seguidors d'Aristoxen de Tàrent), recolzats per l'observació empírica (en contrast amb l'enfocament massa teòric dels pitagòrics).[39][40] Ptolemeu introdueix el cànon harmònic, un aparell experimental que s'utilitzaria per a les demostracions dels capítols següents, després passa a discutir l'afinació pitagòrica. Els pitagòrics creien que les matemàtiques de la música s'havien de basar en la proporció específica de 3:2, mentre que Ptolemeu només creia que només hauria d'implicar tetracords i octaves.[41] Presentà les seves pròpies divisions del tetracord i l'octava, que desenvolupà amb l'ajuda d'un monocord. El llibre acaba amb una exposició més especulativa de les relacions entre l'harmonia, l'ànima (psique) i els planetes (harmonia de les esferes).[42] Tot i que els Harmònics de Ptolemeu no tingueren mai la influència del seu Almagest o Geografia, és un tractat ben estructurat i conté més reflexions metodològiques que qualsevol altre dels seus escrits.[43][44] Durant el Renaixement, les idees de Ptolemeu inspiraren Johannes Kepler en les seves pròpies reflexions sobre l'harmonia del món (Harmonices Mundi, apèndix del llibre V).[45] ÒpticaL'Òptica (en grec antic: Ὀπτικά), és una obra de la qual només en sobrevisqué una versió llatina força pobra, que, al seu torn, fou traduïda per Eugeni de Palerm (ca. 1154) d'una versió àrab perduda. En aquesta obra, Ptolemeu escriu sobre les propietats de la vista (no la llum), incloent-hi la reflexió, la refracció i el color. L'obra és una part important de la història primerenca de l'òptica i influí en el Llibre d'òptica segle xi d'Ibn al-Hàytham.[46] Ptolemeu oferí explicacions per a molts fenòmens relacionats amb la il·luminació i el color, la mida, la forma, el moviment i la visió binocular. També dividí les il·lusions en les provocades per factors físics o òptics i les provocades per factors de judici. Oferí una explicació obscura de la il·lusió del sol o de la lluna (la mida aparent augmentada a l'horitzó) basada en la dificultat de mirar cap amunt.[47][48] El treball es divideix en tres grans apartats. La primera secció (Llibre II) tracta la visió directa des dels principis de la visió i acaba amb una discussió sobre la visió binocular. La segona secció (Llibres III-IV) tracta la reflexió en miralls plans, convexos, còncaus i compostos.[49] L'última secció (llibre V) tracta la refracció i inclou la taula de refracció més antiga que es conserva de l'aire a l'aigua, per a la qual els valors (a excepció de l'angle d'incidència de 60°) mostren signes d'haver estat obtinguts a partir d'una progressió aritmètica.[50] No obstant això, segons Mark Smith, la taula de Ptolemeu es basava en part en experiments reals.[51] La teoria de la visió de Ptolemeu es basava en la idea que els raigs (o flux) que provenien de l'ull formaven un con, el vèrtex es trobava dins de l'ull i la base definia el camp visual. Els raigs eren sensibles i transmetien informació a l'intel·lecte de l'observador sobre la distància i l'orientació de les superfícies. La mida i la forma estaven determinades per l'angle visual subtegut a l'ull combinat amb la distància i l'orientació percebudes.[46][52] Aquesta fou una de les primeres declaracions de la invariància mida-distància com a causa de la mida perceptiva i la constància de la forma, una visió sostinguda pels estoics.[53] FilosofiaEncara que és conegut principalment per les seves contribucions a l'astronomia i altres temes científics, Ptolemeu també participà en discussions epistemològiques i psicològiques en la seva obra.[54] Escrigué un breu assaig titulat Sobre el criteri i l'hegemonikon (en grec antic: Περὶ Κριτηρίου καὶ Ἡγεμονικοῡ), que podria haver estat una de les seves primeres obres. Ptolemeu parla de com els humans obtenen el coneixement científic (és a dir, el «criteri» de la veritat), així com de la naturalesa i l'estructura de la psique o ànima humana, particularment la seva facultat de govern (és a dir, l'hegemonikon).[42] Ptolemeu argumenta que, per arribar a la veritat, s'ha d'utilitzar tant la raó com la percepció dels sentits de manera que es complementin. Sobre el criteri és també destacable per ser l'única de les obres de Ptolemeu en què no parla de matemàtiques.[55] Ptolemeu també afirma la supremacia del coneixement matemàtic sobre altres formes de coneixement. Com Aristòtil, Ptolemeu classifica les matemàtiques com un tipus de filosofia teòrica; tanmateix, Ptolemeu creu que les matemàtiques són superiors a la teologia o la metafísica perquè aquestes darreres són conjecturals mentre que només les primeres poden assegurar certs coneixements. Aquesta visió és contrària a les tradicions platònica i aristotèlica, on la teologia o la metafísica ocupaven el màxim honor.[54] Tot i ser una posició minoritària entre els filòsofs antics, les opinions de Ptolemeu eren compartides per altres matemàtics com Heró d'Alexandria.[56] Llista d'obres
Referències
Bibliografia
Vegeu tambéEnllaços externs
|
||||||||||||||||||||||||||||||||


