|
Latitud La latitud és la distància angular, mesurada sobre un meridià, entre una localització terrestre (o de qualsevol altre planeta) i l'Equador.[1] Es mesura en graus.[2] Normalment per a mesurar l'angle es fa servir la lletra grega fi (φ). La latitud proporciona la ubicació d'un lloc de la Terra, o d'un altre planeta, respecte del nord o sud del seu equador. Així, la latitud pren valors que van des dels 0° en l'equador fins als 90° N del pol Nord o els 90° S del pol Sud. Això suggereix que si es traça una recta que vagi des d'un punt qualsevol de la Terra fins al centre d'aquesta, l'angle que forma aquesta recta amb el pla equatorial expressa la latitud d'aquest punt. L'orientació Nord o Sud depèn de si el punt marcat està per sobre del paral·lel de l'equador (latitud nord) o si està per sota d'aquest paral·lel (latitud Sud).[1] La retícula està formada per les línies de latitud constant i longitud constant, que es construeixen en referència a l'eix de rotació de la Terra. Els punts de referència primaris són els pols on l'eix de rotació de la Terra talla la superfície de referència. Els plans que contenen l'eix de rotació tallen la superfície als meridians; i l'angle entre qualsevol pla meridià i el que passa per Greenwich (el meridià principal) defineix la longitud: els meridians són línies de longitud constant. El pla que passa pel centre de la Terra i perpendicular a l'eix de rotació talla la superfície en un gran cercle anomenat Equador. Plans paral·lels al pla equatorial tallen la superfície en cercles de latitud constant; aquests són els paral·lelismes. L'equador té una latitud de 0°, el pol nord té una latitud de 90° nord (escrit 90° N o +90°), i el pol sud té una latitud de 90° sud (escrita 90° S o −90°). La latitud d'un punt arbitrari és l'angle entre el pla equatorial i la normal a la superfície en aquest punt: la normal a la superfície de l'esfera és al llarg del vector radial. Per si sol, el terme "latitud" normalment es refereix a la latitud geodèsica tal com es defineix a continuació. Breument, la latitud geodèsica d'un punt és l'angle format entre el vector perpendicular (o normal) a la superfície el·lipsoïdal des del punt i el pla de l'equador. ContextS'utilitzen dos nivells d'abstracció en les definicions de latitud i longitud. En el primer pas, la superfície física és modelada pel geoide, una superfície que s'aproxima al nivell mitjà del mar sobre els oceans i la seva continuació sota les masses terrestres. El segon pas és aproximar el geoide mitjançant una superfície de referència matemàticament més senzilla. L'elecció més senzilla per a la superfície de referència és una esfera, però el geoide es modela amb més precisió mitjançant un el·lipsoide de revolució. Les definicions de latitud i longitud en aquestes superfícies de referència es detallen a les seccions següents. Les línies de latitud i longitud constants juntes constitueixen una retícula a la superfície de referència. La latitud d'un punt de la superfície real és la del punt corresponent de la superfície de referència, la correspondència es troba al llarg de la normal a la superfície de referència, que passa pel punt de la superfície física. La latitud i la longitud juntament amb alguna especificació d’alçada constitueixen un sistema de coordenades geogràfiques tal com es defineix a l'especificació de la norma ISO 19111.[3] Com que hi ha molts el·lipsoides de referència diferents, la latitud precisa d'una característica a la superfície no és única: això es subratlla a l'estàndard ISO que estableix que "sense l'especificació completa del sistema de referència de coordenades, les coordenades (és a dir, latitud i longitud) són ambigus en el millor dels casos i sense sentit en el pitjor". Això és de gran importància en aplicacions precises, com ara un sistema de posicionament global (GPS), però en l'ús comú, on no es requereix una alta precisió, l'el·lipsoide de referència no s'acostuma a indicar. En els textos en anglès, l'angle de latitud, definit a continuació, s'acostuma a indicar amb la lletra grega minúscula phi (ϕ o φ). Es mesura en graus, minuts i segons o graus decimals, al nord o al sud de l'equador. A efectes de navegació, les posicions es donen en graus i minuts decimals. Per exemple, el far de The Needles es troba a 50°39.734′ N 001°35.500′ O.[4] Aquest article es refereix als sistemes de coordenades de la Terra: pot ser adaptat per cobrir la Lluna, els planetes i altres objectes celestes (latitud planetographique). DeterminacióEn la navegació celeste, la latitud es determina amb el mètode d'altitud meridià. La mesura més precisa de la latitud requereix una comprensió del camp gravitatori de la Terra, ja sigui per establir teodolits o per determinar les òrbites dels satèl·lits GPS. L'estudi de la figura de la Terra juntament amb el seu camp gravitatori és la ciència de la geodèsia. Latitud a l'esfera La retícula a l'esferaEn la història de la geodèsia s'han utilitzat molts el·lipsoides de referència diferents. En els dies pre-satèl·lit es van idear per donar un bon ajust al geoide sobre l'àrea limitada d'una enquesta, però, amb l'arribada del GPS, s'ha tornat natural utilitzar el·lipsoides de referència (com ara WGS84) amb el centre al centre de massa de la Terra i eix menor alineat amb l'eix de rotació de la Terra. Aquests el·lipsoides geocèntrics solen estar dins de 100 m del geoide. Com que la latitud es defineix respecte a un el·lipsoide, la posició d'un punt donat és diferent a cada el·lipsoide: no es pot especificar exactament la latitud i la longitud d'una característica geogràfica sense especificar l'el·lipsoide utilitzat. Molts mapes que mantenen les agències nacionals es basen en el·lipsoides més antics, de manera que cal saber com es transformen els valors de latitud i longitud d'un el·lipsoide a un altre. Els telèfons GPS són programari per dur a terme transformacions de dades que vinculen WGS84 a l'el·lipsoide de referència local amb la seva quadrícula associada. La latitud, tal com es defineix d'aquesta manera per a l'esfera, sovint s'anomena latitud esfèrica, per evitar ambigüitats amb la latitud geodèsica i les latituds auxiliars definides en seccions posteriors d'aquest article. Latituds amb nom a la Terra A més de l'equador, altres quatre paral·lels són importants:
El pla de l'òrbita de la Terra al voltant del Sol s'anomena eclíptica, i el pla perpendicular a l'eix de rotació de la Terra és el pla equatorial. L'angle entre l'eclíptica i el pla equatorial rep el nom d'inclinació axial, obliqüitat o inclinació de l'eclíptica, i convencionalment es denota amb i. La latitud dels cercles tropicals és igual a i i la latitud dels cercles polars és el seu complement (90° - i). L'eix de rotació varia lentament al llarg del temps i els valors aquí indicats són els de l’època actual. La variació del temps es parla més detalladament a l'article sobre la inclinació axial. La figura mostra la geometria d'una secció transversal del pla perpendicular a l'eclíptica i a través dels centres de la Terra i el Sol al solstici de desembre quan el Sol es troba per sobre en algun punt del tròpic de Capricorn. Les latituds del polar sud per sota del cercle polar antàrtic són a la llum del dia, mentre que les latituds del polar nord per sobre del cercle polar àrtic són de nit. La situació s'inverteix al solstici de juny, quan el Sol es troba al tròpic de càncer. Només a les latituds entre els dos tròpics és possible que el Sol estigui directament a sobre (al zenit). En les projeccions de mapa no hi ha una regla universal sobre com han d'aparèixer meridians i paral·lels. Els exemples a continuació mostren els paral·lels nomenats (com a línies vermelles) en la projecció Mercator comunament utilitzada i la projecció Transverse Mercator. En el primer els paral·lels són horitzontals i els meridians són verticals, mentre que en el segon no existeix una relació exacta de paral·lels i meridians amb horitzontal i vertical: tots dos són corbes complicades.
Latitud a l'el·lipsoideEl·lipsoidesEl 1687 Isaac Newton va publicar els Philosophiæ Naturalis Principia Mathematica, en què demostrava que un cos fluid autogravitatiu giratori en equilibri pren la forma d'un el·lipsoide oblat.[5] (Aquest article fa servir el terme el·lipsoide amb preferència al terme antic esferoide.) El resultat de Newton va ser confirmat per mesures geodèsiques al segle XVIII. (Vegeu arc meridià.) Un el·lipsoide oblat és la superfície tridimensional generada per la rotació d'una el·lipse al voltant del seu eix més curt (eix menor). "El·lipsoide oblat de la revolució" s'abreuja a "el·lipsoide" a la resta d'aquest article. (Els elipsoides que no tenen un eix de simetria s'anomenen triaxials). En la història de la geodèsia s'han utilitzat molts el·lipsoides de referència diferents. En els dies pre-satèl·lit es van idear per donar un bon ajust al geoide sobre l'àrea limitada d'una enquesta, però, amb l'arribada del GPS, s'ha tornat natural utilitzar el·lipsoides de referència (com ara WGS84) amb el centre al centre de massa de la Terra i eix menor alineat amb l'eix de rotació de la Terra. Aquests el·lipsoides geocèntrics solen estar dins de 100 m del geoide. Com que la latitud es defineix respecte a un el·lipsoide, la posició d'un punt donat és diferent a cada el·lipsoide: no es pot especificar exactament la latitud i la longitud d'una característica geogràfica sense especificar l'el·lipsoide utilitzat. Molts mapes que mantenen les agències nacionals es basen en el·lipsoides més antics, de manera que cal saber com es transformen els valors de latitud i longitud d'un el·lipsoide a un altre. Els telèfons GPS són programari per dur a terme transformacions de dades que vinculen WGS84 a l'el·lipsoide de referència local amb la seva quadrícula associada. La geometria de l'el·lipsoide La forma d'un el·lipsoide de revolució ve determinada per la forma de l’el·lipse que gira al voltant del seu eix menor (més curt). Es requereixen dos paràmetres. Un és invariablement el radi equatorial, que és el semieix major, a. L'altre paràmetre sol ser (1) el radi polar o semi-eix menor, b; o (2) el (primer) aplanament, f; o (3) l’excentricitat, e. Aquests paràmetres no són independents: estan relacionats per Molts altres paràmetres (vegeu el·lipse, el·lipsoide) apareixen en l'estudi de la geodèsia, la geofísica i les projeccions cartogràfiques, però tots es poden expressar en termes d'un o dos membres del conjunt a, b, f i e. Tant f com e són petits i sovint són en expansions en sèrie en els càlculs; són de l'ordre1298 respectivament. Els valors d'un nombre d'el·lipsoides es donen a la Figura de la Terra. Els el·lipsoides de referència solen definir-se pel semieix major i l'aplanament invers,
de les quals es deriven
La diferència entre els eixos semimajor i semimenor és d'uns 21 km i com a fracció del semieix major equival a l'aplanament; en un monitor d'ordinador, l'el·lipsoide podria tenir una mida de 300 per 299 píxels. Això amb prou feines es distingiria d'una esfera de 300 per 300 píxels, de manera que les il·lustracions solen exagerar l'aplanament. Latituds geodèsiques i geocèntriques La retícula de l'el·lipsoide es construeix exactament de la mateixa manera que a l'esfera. La normal en un punt de la superfície d'un el·lipsoide no passa pel centre, excepte per als punts de l'equador o dels pols, però la definició de latitud es manté inalterada com a angle entre la normal i el pla equatorial. La terminologia de la latitud s'ha de fer més precisa distingint:
La latitud geogràfica s'ha d'utilitzar amb cura, ja que uns quants autors l'utilitzen com a sinònim de latitud geodèsica mentre que altres l'utilitzen com a alternativa a la latitud astronòmica. "Latitud" (no qualificat) normalment hauria de referir-se a la latitud geodèsica. La importància d'especificar la dada de referència es pot il·lustrar amb un exemple senzill. A l'el·lipsoide de referència per a WGS84, el centre de la Torre Eiffel té una latitud geodèsica de 48° 51′ 29″ N, o 48,8583° N i longitud de 2° 17′ 40″ E o 2,2944°E. Les mateixes coordenades de la dada ED50 defineixen un punt a terra que es troba a 140 m|abbr=off}} de distància de la torre. Una cerca web pot produir uns quants valors diferents per a la latitud de la torre; l'el·lipsoide de referència rarament s'especifica. Els paral·lels o les línies de latitudLes línies de latitud, conegudes com els paral·lels en català quan es refereixen al planeta Terra, són línies horitzontals imaginàries que van d'est a oest (o d'oest a est) sobre els mapes (particularment quan s'utilitza la projecció Mercator) i que s'estenen ja sia cap al nord o cap al sud de l'equador. Tècnicament la latitud es mesura en graus des dels 0° a l'equador (baixa latitud) fins a 90° als pols (90° N o +90° per al pol Nord i 90° S o −90° per al pol Sud). La latitud és aproximadament l'angle que marca el zenit i el sol a l'equinocci. L'angle complementari de la latitud s'anomena colatitud. Efecte de la latitud en el clima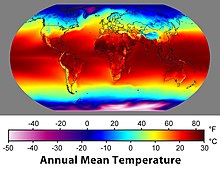 La latitud d'una zona té gran influència sobre el seu clima i la seva meteorologia.[1] A més de l'angle de recepció dels raigs solars també els vents dominants i la presència o absència de les aurores boreals i australs. Unitats de mesura i subdivisionsCada grau de latitud se subdivideix en 60 minuts, cadascun dividit en 60 segons d'arc. És a dir, la latitud s'expressa amb una notació sexagesimal, per exemple la latitud d'un punt s'escriuria com 41° 24′ 7" N (latitud de la ciutat de Barcelona). Una representació alternativa utilitza només graus i minuts, on els segons s'expressen com una fracció decimal dels minuts: així es té 13° 19.717′ N. Els graus també es poden expressar amb els minuts i segons incorporats com a nombre decimal i arrodonit (notació de grau decimal): 13.32861° N. De vegades es reemplaça el sufix nord/sud per signe negatiu pel Sud (−90° per al Pol Sud). Conversió de graus de latitud i longitud en distàncies
Latitud astronòmicaEn aquest cas es mesura l'angle entre el pla equatorial i la superfície normal al geoide. S'origina com l'angle entre l'horitzó i l'estrella polar i només difereix lleugerament de la latitud geodèsica.[6] No s'ha de confondre amb la declinació, que són la localització dels estels al nord i sud de l'equador celestial; ni amb la latitud eclíptica, que descriu les localitzacions al nord i sud de l'eclíptica. Vegeu tambéReferències
|






