|
| Prisekana kocka
|

(animacija)
|
| vrsta |
arhimedsko telo
uniformni polieder
|
| elementi |
F = 14, E = 36,
V = 24 (χ = 2)
|
| stranske ploskve na stran |
8{3} + 6{8}
|
| Conwayjev zapis |
tT
|
| Schläflijev simbol |
t{4,3}
|
| t0,1{4,3}
|
| Wythoffov simbol |
2 3 | 4
|
| Coxeter-Dinkinov diagram |
   
|
| simetrija |
Oh, BC3, [4,3], (*432), red 48
|
| vrtilna grupa |
O, [4,3], (432), red 48
|
| diedrski kot |
3-8: 125º 15' 51′′
8-8: 90º
|
| sklici |
U09, C21, W8
|
| značilnosti |
konveksna
polpravilna
|

obarvane stranske ploskve
|

(slika oglišč)
|
 triakisni oktaeder triakisni oktaeder
(dualni polieder)
|
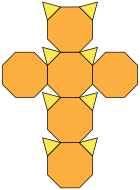
mreža telesa
|
Prisekana kocka (tudi prisekani heksaeder) je v geometriji konveksni polieder. Je arhimedsko telo, eno od trinajstih konveksnih izogonalnih neprizmatičnih teles skonstruirano z dvema ali več vrstami pravilnih mnogokotniških stranskih ploskev.
Ima štirinajst pravilnih stranskih ploskev, od tega osem enakostraničnotrikotniških in šest osemkotniških, ter 36 robov in 24 oglišč. Kadar ima prisekana kocka enotsko dolžino, je to triakisni oktaeder, ki ima robove z dolžino 2 in  . .
Površina in prostornina
Površina P prisekane kocke z dolžino roba a je enaka:

Prostornina V takšne prisekane kocke je:

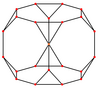
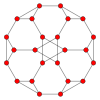
Pravokotne projekcije
Prisekana kocka ima pet posebnih pravokotnih projekcij usrediščenih na oglišče, dve vrsti robov in dve vrsti stranskih ploskev (enakostranični trikotniki in osemkotniki). Zadnji dve odgovarjata Coxeterjevima ravninama B2 in A2.
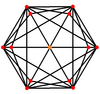
Razvrstitev oglišč
Prisekana kocka ima enako razvrstitev oglišč kot trije nekonveksni uniformni poliedri:
Sorodni poliedri in tlakovanja
sferna/ravninska
simetrija
|
*232
[2,3]
D3h
|
*332
[3,3]
Td
|
*432
[4,3]
Oh
|
*532
[5,3]
Ih
|
*632
[6,3]
P6m
|
*732
[7,3]
|
*832
[8,3]
|
*∞32
[∞,3]
|
red
simetrije
|
12
|
24
|
48
|
120
|
∞
|
Coxeter
Schläfli
|
    
t0,1{2,3}
|
    
t0,1{3,3}
|
    
t0,1{4,3}
|
    
t0,1{5,3}
|
    
t0,1{6,3}
|
    
t0,1{7,3}
|
    
t0,1{8,3}
|
    
t0,1{∞,3}
|
prisekane
oblike
|

3.4.4
|

3.6.6
|

3.8.8
|

3.10.10
|

3.12.12
|

3.14.14
|

3.16.16
|

3.∞.∞
|
triakisne
oblike
|

V3.4.4
|

V3.6.6
|

V3.8.8
|

V3.10.10
|

V3.12.12
|

V3.14.14
|
Družina uniformnih oktaederskih poliedrov
| {4,3}
|
t0,1{4,3}
|
t1{4,3}
|
t0,1{3,4}
|
{3,4}
|
t0,2{4,3}
|
t0,1,2{4,3}
|
{4,3}
|
h0{4,3}
|
h1,2{4,3}
|

|

|

|

|

|

|

|

|

|

|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
Glej tudi
Zunanje povezave
|