古典力学
F
=
d
d
t
(
m
v
)
{\displaystyle {\boldsymbol {F}}={\frac {\mathrm {d} }{\mathrm {d} t}}(m{\boldsymbol {v}})}
運動の第2法則
歴史 (英語版 )
太陽系内惑星の軌道アニメーション。 天体力学 (てんたいりきがく、英 : celestial mechanics )[ 1] 万有引力の法則 に従う天体 の運動を古典力学 に基づいて扱う学問である。ニュートン力学 から成立した物理学 の一分野であり、また位置天文学 と並び古典天文学 の一角を占める[ 3]
惑星 の公転 運動は主に太陽 の重力 によって支配されている(ケプラーの法則 )ものの、他の惑星などが及ぼす重力が摂動 として無視できない影響を及ぼすため、天体力学ではそのような摂動を解析的に取り扱う摂動論 が発達した。その最も単純かつ非自明な問題が三体問題 である。月 の運動は暦 の編纂(へんさん)や航海術 への応用という実用的な目的のためにとりわけ精確な予測が求められる一方で、惑星の運動に比べ摂動が大きく影響するため、太陰運動論 は何世代にも渡って改良されてきた。また天王星 の観測データの異常から海王星 の存在を予言しその位置を予測したことでも知られる。
天体力学は軌道共鳴 、太陽系の安定性 、自転 軸の歳差 と章動 、惑星の平衡形状、自転と公転の同期 といった問題をも扱う。20世紀には人工衛星 ・宇宙探査機 の軌道設計 および軌道制御 を扱う軌道力学 が派生し、また天体力学の適用対象も太陽系 から惑星形成 、ブラックホール 、そして球状星団 および銀河 などへと拡大した。
中心天体(例えば太陽 )からの重力 (万有引力の法則 )を受ける天体(例えば惑星 )の運動はケプラー運動 と呼ばれる[ 4]
r
{\displaystyle \mathbf {r} }
ニュートンの運動方程式
d
2
r
d
t
2
=
−
μ
r
|
r
|
3
{\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=-\mu {\frac {\mathbf {r} }{|\mathbf {r} |^{3}}}}
を満足する。
μ
{\displaystyle \mu }
重力定数 と中心天体の質量 と問題の天体の質量の和の積である[ 注釈 1]
M
⊙
{\displaystyle M_{\odot }}
G
{\displaystyle {\mathcal {G}}}
ガウス引力定数
k
{\displaystyle k}
m
{\displaystyle m}
μ
=
k
2
(
1
+
m
)
{\displaystyle \mu =k^{2}(1+m)}
が成立する。また時刻の単位としては日 (ユリウス日 )が、距離の単位としては天文単位 が使われる。
ケプラーの法則 [ 15] 軌道 の最も基本的な性質を述べたものである(これは惑星のまわりを運動する衛星 に関しても成立する)。
第1法則: 惑星は太陽をひとつの焦点 とする楕円 軌道を描く。
第2法則: 太陽と惑星を結ぶ線分が単位時間に掃く面積(面積速度 )は一定である。
第3法則: 惑星の公転周期の二乗は軌道長半径の三乗に比例する。 離心率
e
=
0.5
{\displaystyle e=0.5}
第1法則が主張する楕円軌道の形状は長半径 (英 : semi-major axis )
a
{\displaystyle a}
離心率 (英 : eccentricity )
e
{\displaystyle e}
近点 (英 : pericenter ) と呼ぶが[ 18] 近日点 (英 : perihelion )[ 19] 近地点 (英 : perigee )[ 20] 遠点 (英 : apocenter ) である[ 21]
r
{\displaystyle r}
アプス線 (英語版 )
f
{\displaystyle f}
r
(
f
)
=
a
(
1
−
e
2
)
1
+
e
cos
f
{\displaystyle r(f)={\frac {a(1-e^{2})}{1+e\cos f}}}
と表示される。角
f
{\displaystyle f}
真近点角 または真近点離角 (英 : true anomaly ) と呼ばれる[ 23] #軌道要素 節を参照)。なお
p
=
a
(
1
−
e
2
)
{\displaystyle p=a(1-e^{2})}
英 : semilatus rectum ) と呼ぶ。
第2法則は角運動量 の保存を意味する。第3法則に対応して、長半径
a
{\displaystyle a}
平均運動 (英 : mean motion )
n
=
2
π
T
{\displaystyle n={\frac {2\pi }{T}}}
(
T
{\displaystyle T}
n
2
a
3
=
μ
{\displaystyle n^{2}a^{3}=\mu }
ケプラー運動には楕円軌道の他に放物線 軌道、双曲線 軌道が存在する。これらはいずれも円錐曲線 である。
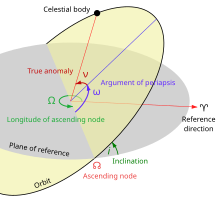
軌道傾斜角
i
{\displaystyle i}
Ω
{\displaystyle \Omega }
ω
{\displaystyle \omega }
ν
{\displaystyle \nu }
天体の軌道およびその上の位置を特定するために用いられるパラメータを軌道要素 (英 : orbital element ) と呼ぶ[ 32] 長半径
a
{\displaystyle a}
離心率
e
{\displaystyle e}
近点引数 (英 : argument of pericenter )[ 33]
ω
{\displaystyle \omega }
軌道傾斜角 (英 : inclination )[ 35]
i
{\displaystyle i}
昇交点黄経 (英 : longitude of ascending node )[ 36]
Ω
{\displaystyle \Omega }
i
{\displaystyle i}
黄道面 [ 36] 不変面 )となす角として定義される[ 35] 春分点 [ 38] 黄経 )が昇交点黄経
Ω
{\displaystyle \Omega }
[ 36]
ω
{\displaystyle \omega }
[ 33]
ω
{\displaystyle \omega }
ϖ
=
Ω
+
ω
{\displaystyle \varpi =\Omega +\omega }
により定義される近点黄経 (英 : longitude of pericenter ) を採用してもよい[ 33]
楕円軌道上の天体の位置を表す角度として真近点角
f
{\displaystyle f}
離心近点角 (離心近点離角, 英 : eccentric anomaly )[ 23]
E
{\displaystyle E}
平均近点角 (平均近点離角, 英 : mean anomaly )
M
{\displaystyle M}
平均黄経 (英 : mean longitude )
λ
{\displaystyle \lambda }
E
{\displaystyle E}
r
=
a
(
1
−
e
cos
E
)
{\displaystyle r=a(1-e\cos E)}
を満足し、真近点角
f
{\displaystyle f}
tan
f
2
=
1
+
e
1
−
e
tan
E
2
{\displaystyle \tan {\frac {f}{2}}={\sqrt {\frac {1+e}{1-e}}}\tan {\frac {E}{2}}}
という関係にある。平均近点角
M
{\displaystyle M}
t
0
{\displaystyle t_{0}}
M
=
n
(
t
−
t
0
)
{\displaystyle M=n(t-t_{0})}
E
{\displaystyle E}
ケプラー方程式
E
−
e
sin
E
=
M
{\displaystyle E-e\sin E=M}
によって結ばれる。平均黄経
λ
{\displaystyle \lambda }
λ
=
M
+
Ω
+
ω
=
M
+
ϖ
{\displaystyle \lambda =M+\Omega +\omega =M+\varpi }
により定義される。これらの角
f
{\displaystyle f}
E
{\displaystyle E}
M
{\displaystyle M}
λ
{\displaystyle \lambda }
t
0
{\displaystyle t_{0}}
元期 (英 : epoch ) での平均黄経
ϵ
{\displaystyle \epsilon }
t
{\displaystyle t}
t
0
{\displaystyle t_{0}}
{
a
,
e
,
i
,
t
0
,
ω
,
Ω
}
{\displaystyle \{a,e,i,t_{0},\omega ,\Omega \}}
[ 42]
具体的な太陽系惑星の軌道要素の値は#太陽系惑星の軌道要素 節および#月の軌道要素 節を参照。
ある瞬間における天体の座標
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
(
v
x
,
v
y
,
v
z
)
{\displaystyle (v_{x},v_{y},v_{z})}
赤道座標 では赤緯
α
{\displaystyle \alpha }
赤経
δ
{\displaystyle \delta }
[ 46] 軌道決定 (英語版 ) [ 47]
惑星の公転軌道は第一に太陽の重力によって支配されており、0次近似としては太陽-惑星の二体問題とみなすことができる。この近似では惑星の軌道要素は一定であり、時間変化しない。しかし実際には惑星の軌道は他の惑星の摂動 (英 : perturbation ) によって変化する[ 48] 接触軌道要素 (英 : osculating orbital elements )[ 50] 英 : variation of arbitrary constants ) である。
摂動として働く力が重力などの保存力 である場合、天体の運動方程式は摂動関数 または擾乱関数 (英 : disturbing function または 英 : perturbation function ) として知られる関数
R
{\displaystyle R}
d
2
r
d
t
2
+
μ
r
|
r
|
3
=
∂
R
∂
r
{\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}+\mu {\frac {\mathbf {r} }{|\mathbf {r} |^{3}}}={\frac {\partial R}{\partial \mathbf {r} }}}
と書くことができる。例えば太陽系惑星の場合、
i
{\displaystyle i}
英 : heliocentric coordinate system ) での位置
r
i
{\displaystyle \mathbf {r} _{i}}
d
2
r
i
d
t
2
+
k
2
(
1
+
m
i
)
r
i
|
r
i
|
3
=
∂
R
i
∂
r
i
{\displaystyle {\frac {d^{2}\mathbf {r} _{i}}{dt^{2}}}+k^{2}(1+m_{i}){\frac {\mathbf {r} _{i}}{|\mathbf {r} _{i}|^{3}}}={\frac {\partial R_{i}}{\partial \mathbf {r} _{i}}}}
R
i
=
k
2
∑
j
≠
i
m
j
(
1
|
r
i
−
r
j
|
−
r
i
⋅
r
j
|
r
j
|
3
)
{\displaystyle R_{i}=k^{2}\sum _{j\neq i}m_{j}\left({\frac {1}{|\mathbf {r} _{i}-\mathbf {r} _{j}|}}-{\frac {\mathbf {r} _{i}\cdot \mathbf {r} _{j}}{|\mathbf {r} _{j}|^{3}}}\right)}
を満足する。ここに
m
i
{\displaystyle m_{i}}
i
{\displaystyle i}
英 : direct term )、第2項を間接項 (英 : indirect term ) と呼ぶ。
摂動関数
R
{\displaystyle R}
σ
j
{\displaystyle \sigma _{j}}
ラグランジュの惑星方程式
∑
k
=
1
6
[
σ
j
,
σ
k
]
d
σ
k
d
t
=
∂
R
∂
σ
j
(
j
=
1
,
2
,
…
,
6
)
{\displaystyle \sum _{k=1}^{6}[\sigma _{j},\sigma _{k}]{\frac {d\sigma _{k}}{dt}}={\frac {\partial R}{\partial \sigma _{j}}}\ \ (j=1,2,\ldots ,6)}
によって記述される。ここに
[
c
j
,
c
k
]
{\displaystyle [c_{j},c_{k}]}
ラグランジュ括弧 である。接触軌道要素として
σ
j
=
{
a
,
e
,
i
,
ϵ
,
ϖ
,
Ω
}
{\displaystyle \sigma _{j}=\{a,e,i,\epsilon ,\varpi ,\Omega \}}
d
a
d
t
=
+
2
n
a
∂
R
∂
ϵ
{\displaystyle {\frac {da}{dt}}=+{\frac {2}{na}}{\frac {\partial R}{\partial \epsilon }}}
d
e
d
t
=
−
1
−
e
2
n
a
2
e
[
1
−
1
−
e
2
]
∂
R
∂
ϵ
−
1
−
e
2
n
a
2
e
∂
R
∂
ϖ
{\displaystyle {\frac {de}{dt}}=-{\frac {\sqrt {1-e^{2}}}{na^{2}e}}[1-{\sqrt {1-e^{2}}}]{\frac {\partial R}{\partial \epsilon }}-{\frac {\sqrt {1-e^{2}}}{na^{2}e}}{\frac {\partial R}{\partial \varpi }}}
d
i
d
t
=
−
tan
(
i
/
2
)
n
a
2
1
−
e
2
(
∂
R
∂
ϵ
+
∂
R
∂
ϖ
)
−
1
n
a
2
1
−
e
2
sin
i
∂
R
∂
Ω
{\displaystyle {\frac {di}{dt}}=-{\frac {\tan(i/2)}{na^{2}{\sqrt {1-e^{2}}}}}\left({\frac {\partial R}{\partial \epsilon }}+{\frac {\partial R}{\partial \varpi }}\right)-{\frac {1}{na^{2}{\sqrt {1-e^{2}}}\sin i}}{\frac {\partial R}{\partial \Omega }}}
d
ϵ
d
t
=
−
2
n
a
∂
R
∂
a
+
1
−
e
2
n
a
2
e
[
1
−
1
−
e
2
]
∂
R
∂
e
+
tan
(
i
/
2
)
n
a
2
1
−
e
2
∂
R
∂
i
{\displaystyle {\frac {d\epsilon }{dt}}=-{\frac {2}{na}}{\frac {\partial R}{\partial a}}+{\frac {\sqrt {1-e^{2}}}{na^{2}e}}[1-{\sqrt {1-e^{2}}}]{\frac {\partial R}{\partial e}}+{\frac {\tan(i/2)}{na^{2}{\sqrt {1-e^{2}}}}}{\frac {\partial R}{\partial i}}}
d
ϖ
d
t
=
+
1
−
e
2
n
a
2
e
∂
R
∂
e
+
tan
(
i
/
2
)
n
a
2
1
−
e
2
∂
R
∂
i
{\displaystyle {\frac {d\varpi }{dt}}=+{\frac {\sqrt {1-e^{2}}}{na^{2}e}}{\frac {\partial R}{\partial e}}+{\frac {\tan(i/2)}{na^{2}{\sqrt {1-e^{2}}}}}{\frac {\partial R}{\partial i}}}
d
Ω
d
t
=
+
1
n
a
2
1
−
e
2
sin
i
∂
R
∂
i
{\displaystyle {\frac {d\Omega }{dt}}=+{\frac {1}{na^{2}{\sqrt {1-e^{2}}}\sin i}}{\frac {\partial R}{\partial i}}}
摂動関数
R
{\displaystyle R}
カール・フリードリヒ・ガウス による方法は摂動関数ではなく天体に働く力を陽に扱うものであり、非保存力を扱うことができる。この場合、運動方程式を
d
2
r
d
t
2
=
−
μ
r
|
r
|
3
+
F
(
t
,
r
,
r
˙
)
{\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=-\mu {\frac {\mathbf {r} }{|\mathbf {r} |^{3}}}+\mathbf {F} (t,\mathbf {r} ,{\dot {\mathbf {r} }})}
と書くとき、
I
=
I
(
r
,
r
˙
)
{\displaystyle I=I(\mathbf {r} ,{\dot {\mathbf {r} }})}
d
I
d
t
=
∂
I
∂
r
˙
⋅
F
{\displaystyle {\frac {dI}{dt}}={\frac {\partial I}{\partial {\dot {\mathbf {r} }}}}\cdot \mathbf {F} }
により与えられる。摂動
F
{\displaystyle \mathbf {F} }
動径成分
R
′
{\displaystyle R'}
R
′
{\displaystyle R'}
S
′
{\displaystyle S'}
W
′
{\displaystyle W'}
軌道の接成分
T
′
{\displaystyle T'}
T
′
{\displaystyle T'}
N
′
{\displaystyle N'}
W
′
{\displaystyle W'}
前者の立場では、軌道要素
{
a
,
e
,
i
,
Ω
,
ω
,
t
0
}
{\displaystyle \{a,e,i,\Omega ,\omega ,t_{0}\}}
p
{\displaystyle p}
d
a
d
t
=
p
μ
2
a
1
−
e
2
{
e
sin
f
R
′
+
p
r
S
′
}
{\displaystyle {\frac {da}{dt}}={\sqrt {\frac {p}{\mu }}}{\frac {2a}{1-e^{2}}}\left\{e\sin fR'+{\frac {p}{r}}S'\right\}}
d
e
d
t
=
p
μ
{
sin
f
R
′
+
(
cos
f
+
cos
E
)
S
′
}
{\displaystyle {\frac {de}{dt}}={\sqrt {\frac {p}{\mu }}}\left\{\sin fR'+(\cos f+\cos E)S'\right\}}
d
i
d
t
=
r
cos
(
f
+
ω
)
n
a
2
1
−
e
2
W
′
{\displaystyle {\frac {di}{dt}}={\frac {r\cos(f+\omega )}{na^{2}{\sqrt {1-e^{2}}}}}W'}
d
Ω
d
t
=
r
sin
(
f
+
ω
)
n
a
2
1
−
e
2
sin
i
W
′
{\displaystyle {\frac {d\Omega }{dt}}={\frac {r\sin(f+\omega )}{na^{2}{\sqrt {1-e^{2}}}\sin i}}W'}
d
ω
d
t
=
1
e
p
μ
{
−
cos
f
R
′
+
(
1
+
r
p
)
sin
f
S
′
}
−
cos
i
d
Ω
d
t
{\displaystyle {\frac {d\omega }{dt}}={\frac {1}{e}}{\sqrt {\frac {p}{\mu }}}\left\{-\cos fR'+\left(1+{\frac {r}{p}}\right)\sin fS'\right\}-\cos i{\frac {d\Omega }{dt}}}
d
t
0
d
t
=
−
1
−
e
2
n
2
a
e
{
(
cos
f
−
2
e
r
p
)
R
′
−
(
1
+
r
p
)
sin
f
S
′
}
−
3
2
a
(
t
−
t
0
)
d
a
d
t
{\displaystyle {\frac {dt_{0}}{dt}}=-{\frac {1-e^{2}}{n^{2}ae}}\left\{\left(\cos f-2e{\frac {r}{p}}\right)R'-\left(1+{\frac {r}{p}}\right)\sin fS'\right\}-{\frac {3}{2a}}(t-t_{0}){\frac {da}{dt}}}
離心率
e
{\displaystyle e}
i
{\displaystyle i}
R
{\displaystyle R}
[ 82]
M
{\displaystyle M}
λ
{\displaystyle \lambda }
[ 82]
R
=
∑
C
(
a
,
e
,
I
,
a
′
,
e
′
,
I
′
)
cos
θ
{\displaystyle R=\sum C(a,e,I,a',e',I')\cos \theta }
θ
=
j
1
λ
+
j
2
ϖ
+
j
3
Ω
+
j
1
′
λ
′
+
j
2
′
ϖ
′
+
j
3
′
Ω
′
{\displaystyle \theta =j_{1}\lambda +j_{2}\varpi +j_{3}\Omega +j_{1}'\lambda '+j_{2}'\varpi '+j_{3}'\Omega '}
(プライムなしが注目天体の軌道要素、プライムありがもう一方の天体の軌道要素)という形に展開される。軌道要素の時間変化は、周期摂動とそれより長い時間スケールでの時間変化を引き起こす(英 : secular perturbation )[ 87] [ 48]
j
1
{\displaystyle j_{1}}
j
1
′
{\displaystyle j_{1}'}
永年項 , 英 : secular term )が存在し近点移動 が生じる。一方で、離心率と軌道傾斜角には永年項が存在せず非常に長い周期で時間変化する。
天体力学のいくつかの問題(ラグランジュの惑星方程式の導出、軌道共鳴の議論など)にはケプラーの軌道要素ではなく正準共役量を基本変数として用いるハミルトン力学 が適している。例えばドロネー変数
(
l
,
g
,
h
,
L
,
G
,
H
)
{\displaystyle (l,g,h,L,G,H)}
l
=
M
,
L
=
μ
a
{\displaystyle l=M,\ \ L={\sqrt {\mu a}}}
g
=
ω
,
G
=
μ
a
(
1
−
e
2
)
{\displaystyle g=\omega ,\ \ G={\sqrt {\mu a(1-e^{2})}}}
h
=
Ω
,
H
=
μ
a
(
1
−
e
2
)
cos
I
{\displaystyle h=\Omega ,\ \ H={\sqrt {\mu a(1-e^{2})}}\cos I}
により定義され、
(
l
,
L
)
{\displaystyle (l,L)}
(
g
,
G
)
{\displaystyle (g,G)}
(
h
,
H
)
{\displaystyle (h,H)}
F
=
−
μ
2
2
L
2
{\displaystyle F=-{\frac {\mu ^{2}}{2L^{2}}}}
により与えられる。なおこれらの変数はケプラー問題の作用・角変数 と関係している[ 99]
正準形式の摂動論は摂動後のハミルトニアン から角変数を消去するような正準変換 を構築することによって実現される。このような正準変換を施すと、変換後の作用変数が時間変化しなくなり、問題を自明に解くことができる。このような変換は摂動の任意の次数まで続けることができるものの、この摂動級数は収束せず、級数を途中で打ち切る必要がある(この事情は定数変化法により得られる摂動級数でも同じである)。
月の満ち欠け(月相 )は太陰暦 および太陰太陽暦 の基礎であり[ 101] [ 102] 月の軌道 は等速円運動ではなく、そこからのずれ(不等 , 英 : inequality )が存在する[ 103] 中心差 (英語版 ) 英 : equation of the center ) であるが[ 103]
出差 (英語版 ) 英 : evection ): 遠地点または近地点が太陽の向きにあるとき、相対的に強い摂動を受ける効果[ 103] 二均差 (英語版 ) 英 : variation ): 1朔望月 の間に太陽の摂動によって地球の重力が実効的に変化する効果[ 103] 年差 (英 : annual equation ): 地球の離心率のために一年の間に太陽の摂動の強さが変化する効果[ 103] これらの不等を説明し、精度よく月の運動を予測することは太陰運動論 (英語版 ) [ 104] [ 105] 英 : lunar theory ) として古くから調べられてきた。これには純粋な天文学上の興味に加えて、航海術(経度 の測定)への応用という実用的な目的があった。月の理論は最も一般には他の惑星の摂動や地球や月が球形でないことの効果を考慮する必要があるが、アーネスト・ウィリアム・ブラウン は太陽、地球、月の三体を質点として扱う場合論を太陰運動論の main problem と呼んだ。月の運動は惑星の運動に比べて顕著に大きな摂動を受けており[ 104]
またエドモンド・ハレー によって指摘された、古代から続く月食の記録を比較すると月の平均運動が徐々に増大しているように見えるという永年加速 の問題がある。ラプラス、アダムズを含む数世代にわたる長い論争を経て、潮汐摩擦によって地球の自転が減速し時刻の定義自体が変化している効果を考慮することによって永年加速の問題は解決された。
同一の中心天体のまわりの2つの公転軌道について、その平均運動が簡単な整数比にあるとき尽数関係 (英 : commensurable ) にあるという[ 112] 平均運動共鳴 と呼ばれる[ 113]
A
{\displaystyle A}
B
{\displaystyle B}
p
{\displaystyle p}
q
{\displaystyle q}
p
n
A
−
q
n
B
+
(
q
−
p
)
ϖ
˙
A
=
0
{\displaystyle pn_{A}-qn_{B}+(q-p){\dot {\varpi }}_{A}=0}
が成立することを言う(通常第3項は小さな値であり落としてよい)。例えば小惑星帯 のカークウッドの空隙 と呼ばれる小惑星の数が少ない領域は木星と平均運動共鳴にあり不安定化したものだと考えられている[ 115] 共鳴外縁天体 と呼ばれる海王星 と平均運動共鳴にある天体群が存在することが知られており、その代表的なものが2:3の平均運動共鳴にある冥王星 である[ 116] ラプラス共鳴 と呼び、太陽系では木星 系のイオ -エウロパ -ガニメデ が唯一の例である[ 117]
一方、平均運動共鳴とは異なり、永年摂動による近点移動の振動数が摂動天体の固有振動数と尽数関係にあるときは永年共鳴 (英 : secular resonance ) として知られている[ 118] [ 118]
太陽系惑星の軌道が長期的に安定して保たれるかという太陽系の安定性 (英語版 ) アイザック・ニュートン 以来研究されてきた。ニュートンは太陽系は不安定であると考えていた[ 121]
blind Fate could never make all the Planets move one and the same way in Orbs concentrick, some inconsiderable Irregularities excepted, which may have risen from the mutual Actions of Comets and Planets upon one another, and which will be apt to increase, till this System wants a Reformation. Such a wonderful Uniformity in the Planetary System must be allowed the Effect of Choice. (盲目の運命はすべての惑星を同心円状の軌道上を同じように動かすことはできない。彗星や惑星の相互作用から生じると考えられるわずかな不規則性は増大しつづけ、終には再構築が必要になるだろう。惑星系の驚くべき一様性は神による選択の帰結でなければならない。) — アイザック・ニュートン、Opticks (1706)
ラグランジュらによる摂動論の研究を経て、ラプラスは1776年に永年摂動の1次の範囲では惑星の軌道長半径は時間変化せず安定であることを示した。シメオン・ドニ・ポアソン はラプラスの結果を拡張し、1808年に2次摂動の範囲でも軌道長半径は永年不変量であることを示した。しかしユルバン・ルヴェリエ は1840年から41年にかけて、長期間の軌道進化では高次の摂動が重要であり、摂動の低次の項だけに基づくラプラスらによる安定性の証明は信頼できないと指摘した(同時に小分母の問題 にも言及している)。アンリ・ポアンカレ はルヴェリエの問題提起を受けて、1880年代に惑星系の軌道は解析的な解の表示が存在しないこと(ポアンカレの定理 )、そして問題の摂動級数は一般に発散することを証明した。1960年代のコルモゴロフらによるKAM理論 は近可積分系 の大部分の軌道は摂動が十分に小さければトーラス上の準周期解となることを示しており、太陽系の安定性をこの路線で証明する研究が行われた。
一方で、1950年頃からは電子計算機による太陽系の長時間高精度シミュレーションが行われるようになった。初期のものとしては1951年の W. J. Eckert らによる5惑星シミュレーションがある[ 129] リャプノフ時間 500万年で不安定化すると主張した[ 131] [ 132] [ 133]
多くの天体は公転 に加えて自転 しており、自転運動はオイラーの運動方程式 によって記述される。測地学 では地球の自転を地球に対して固定された座標系で議論することが多いものの、天文学分野では慣性系を用いて議論することが好まれる。惑星の自転はある軸(自転軸 )まわりの回転として表現でき、その軸を
n
{\displaystyle \mathbf {n} }
ω
{\displaystyle \omega }
ω
=
ω
n
{\displaystyle {\boldsymbol {\omega }}=\omega \mathbf {n} }
L
{\displaystyle \mathbf {L} }
L
=
I
ω
{\displaystyle \mathbf {L} =\mathbf {I} {\boldsymbol {\omega }}}
I
{\displaystyle \mathbf {I} }
慣性モーメント テンソル
I
i
j
=
∫
ρ
(
|
x
|
2
δ
i
j
−
x
i
x
j
)
d
3
x
{\displaystyle I_{ij}=\int \rho (|\mathbf {x} |^{2}\delta _{ij}-x_{i}x_{j})d^{3}x}
である。しばしば座標系として慣性主軸を取り、そのとき慣性モーメントテンソルは主慣性モーメント
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
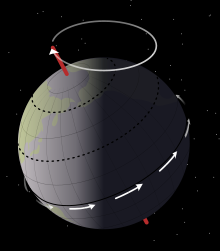
地球の自転軸の回転運動が歳差である。 地球の自転軸は月と太陽および他の惑星による摂動を受け、複雑に変化する。このうち長周期での軸の移動を歳差 (英 : precession )、より短周期での振動を章動 (英 : nutation ) と呼ぶ。歳差の周期は約2万6000年であり、春分点 の移動をもたらす。章動のうちもっとも振幅の大きな成分は周期18.6年であり、月の昇交点がこの周期で移動していることによる。歳差および章動は木下宙 によって1977年に精密な理論が構築された[ 146]
潮汐力 (英 : tidal force )[ 147] 潮汐 の原因として知られている[ 149] [ 150] [ 149]
V
t
i
d
a
l
=
−
ζ
g
P
2
(
cos
ψ
)
{\displaystyle V_{\mathrm {tidal} }=-\zeta gP_{2}(\cos \psi )}
ζ
=
m
s
m
p
(
R
p
a
)
3
R
p
{\displaystyle \zeta ={\frac {m_{\mathrm {s} }}{m_{\mathrm {p} }}}\left({\frac {R_{\mathrm {p} }}{a}}\right)^{3}R_{\mathrm {p} }}
により与えられる。ここに
R
p
{\displaystyle R_{\mathrm {p} }}
m
p
{\displaystyle m_{\mathrm {p} }}
m
s
{\displaystyle m_{\mathrm {s} }}
a
{\displaystyle a}
g
=
G
m
p
R
p
2
{\displaystyle g={\frac {{\mathcal {G}}m_{\mathrm {p} }}{R_{\mathrm {p} }^{2}}}}
ψ
{\displaystyle \psi }
P
2
{\displaystyle P_{2}}
ルジャンドル多項式 である。
潮汐による海水の移動が生じる摩擦(潮汐摩擦 、英 : tidal friction )は地球の自転を減速させる[ 152] [ 152]
惑星は厳密には球形ではなく、自転による変形および潮汐力による潮汐変形 [ 149]
ψ
{\displaystyle \psi }
P
2
(
cos
ψ
)
{\displaystyle P_{2}(\cos \psi )}
ラブ数 (英語版 )
主慣性モーメント
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
重力ポテンシャル
Φ
{\displaystyle \Phi }
Φ
=
−
G
M
r
−
G
(
A
+
B
+
C
−
3
I
)
2
r
3
{\displaystyle \Phi =-{\frac {{\mathcal {G}}M}{r}}-{\frac {{\mathcal {G}}(A+B+C-3I)}{2r^{3}}}}
はマッカラーの公式 と呼ばれる。ここに
I
{\displaystyle I}
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
I
=
A
x
2
+
B
y
2
+
C
z
2
r
2
{\displaystyle I={\frac {Ax^{2}+By^{2}+Cz^{2}}{r^{2}}}}
により与えられる。
月は常に同じ面を地球に向けているものの、秤動 による変化がある。 月は(秤動 (英 : libration ) を除き)常に同じ面を地球に向けているが、これは月の自転周期と公転周期が同期しているためである。これは地球の重力による月の潮汐変形が原因であり[ 160] [ 162]
重力相互作用する3天体の運動を求める問題は三体問題 として知られる。第三体の質量が他の二体に比べて極めて小さく、二体に及ぼす重力が無視できるとき制限三体問題 と呼び、特に二体が円運動するときを円制限三体問題と呼ぶ。この問題は多くの人の手によって調べられてきており、三体問題は求積法 により解くことはできないものの[ 166] ラグランジュ点 はよく知られている[ 167]
土星 や天王星 に存在する環 は衛星と相互に重力を及ぼし合う。環の構造や安定性、羊飼い衛星 [ 169]
木星による摂動を受ける彗星の軌道のシミュレーション。図中の赤点が太陽、黒点が木星、青点が彗星を表す。距離および時間の単位は木星公転運動の半径および周期。薄い青色の楕円が初期の軌道、濃い青の楕円が摂動後の軌道である。 彗星 は大きな離心率を持ち、特に極端なものはサングレーザー と呼ばれる[ 172] ティスランの判定式 によって彗星の同一性を判定できる。また彗星が大きな離心率を獲得する機構として古在メカニズム が提案されている[ 172]
小惑星 などの太陽系小天体 の軌道はカオス を示すことでも注目される。小惑星帯 の小惑星の多くは小惑星-木星系の、または小惑星-木星-土星系の平均運動共鳴に由来するカオス軌道を持つ[ 175] カオス拡散 といった効果を生じる[ 175]
また宇宙塵 などの小天体の場合、輻射圧 などの重力以外の摂動が軌道進化において重要である場合がある[ 176]
厳密には天体は球形 ではなく、それに対応して天体の重力ポテンシャル には単極子項への補正が存在する(多重極展開 (英語版 ) 人工衛星 の軌道に最も大きな摂動として寄与するため、軌道力学 では重力ポテンシャルの補正を考慮する必要がある[ 177]
Φ
{\displaystyle \Phi }
M
{\displaystyle M}
R
{\displaystyle R}
J
l
{\displaystyle J_{l}}
ルジャンドル多項式
P
l
{\displaystyle P_{l}}
Φ
(
r
,
θ
,
φ
)
=
−
G
M
r
{
1
−
∑
l
=
2
∞
J
l
(
R
r
)
l
P
l
(
cos
θ
)
}
{\displaystyle \Phi (r,\theta ,\varphi )=-{\frac {{\mathcal {G}}M}{r}}\left\{1-\sum _{l=2}^{\infty }J_{l}\left({\frac {R}{r}}\right)^{l}P_{l}(\cos \theta )\right\}}
と書ける。
強重力場のもとでは一般相対性理論 によるニュートン重力からの補正が必要となる。これは水星の近日点移動の要因のひとつとして有名である。例えばシュワルツシルト時空 におけるハミルトン–ヤコビ方程式 は
−
1
1
−
2
M
/
r
(
∂
S
∂
t
)
2
+
(
1
−
2
M
r
)
(
∂
S
∂
r
)
2
+
1
r
2
(
∂
S
∂
θ
)
2
+
1
r
2
sin
2
θ
(
∂
S
∂
ϕ
)
2
+
1
=
0
{\displaystyle -{\frac {1}{1-2M/r}}\left({\frac {\partial S}{\partial t}}\right)^{2}+\left(1-{\frac {2M}{r}}\right)\left({\frac {\partial S}{\partial r}}\right)^{2}+{\frac {1}{r^{2}}}\left({\frac {\partial S}{\partial \theta }}\right)^{2}+{\frac {1}{r^{2}\sin ^{2}\theta }}\left({\frac {\partial S}{\partial \phi }}\right)^{2}+1=0}
と書ける。一般相対論効果はブラックホール などのコンパクト天体 で顕著であり、銀河中心 の恒星の運動は超大質量ブラックホール の一般相対論効果を強く受ける[ 182] 連星パルサー を代表とするコンパクト星連星では重力波 放出により軌道が収縮する[ 183] [ 184]
惑星形成理論は微惑星 の集積として惑星が形成される過程を議論するものであり、微惑星 の合体成長過程は天体力学と関係している。
恒星系力学 (英語版 ) 恒星 からなる系を取り扱う理論であり、球状星団 や銀河 の力学的な性質の基礎となる[ 186] 統計力学 およびプラズマ物理学 とも関係している[ 186]
1576年から1601年にかけて、ティコ・ブラーエ (1546-1601) はデンマーク (ウラニボリ )、次いでチェコ のプラハ において太陽 と惑星 を観測し、望遠鏡 がない当時としては最高精度の誤差1 - 2分角でその位置をした。ヨハネス・ケプラー (1571-1630) はブラーエの観測結果をもとにケプラーの法則 に到達し、1609年の『新天文学 (英語版 ) [ 188] 羅 : Astronomia nova 宇宙の調和 (英語版 ) [ 189] 羅 : Harmonice Mundi
エドモンド・ハレー (1656-1742) の勧めもあり、1687年にアイザック・ニュートン (1642-1727) は『自然哲学の数学的諸原理 』(プリンキピア、羅 : Philosophiæ Naturalis Principia Mathematica ニュートン力学 および天体力学の基礎を築いた。なおニュートンがプリンキピアを書き上げるにあたって、ロバート・フック (1635-1703) やジョン・フラムスティード (1646-1719) ら同時代の研究者の業績に大きく影響を受けている。
まず第1巻でニュートンは質量 (quantity of matter) および運動量 (quantity of motion) を定義し、力 (force) について論じている。続いて運動の法則 を定式化し、中心力 場のもとでは面積速度 が一定であること(そして逆に面積速度が一定であるならば中心力が働いていること)、円錐曲線 を描いて運動する物体には距離の二乗に反比例する中心力が作用していること、その場合に楕円軌道を描く物体の周期は楕円の長半径の1.5乗に比例することを示した。
さらにニュートンは互いに引力を及ぼす二体問題 についても論じ、その重心 まわりの運動に帰着できることを示し、逆二乗則の場合には重心まわりの軌道は円錐曲線となることを主張した(ただし逆二乗則から楕円軌道が導かれることの証明をプリンキピアの初版では与えず、後の版では証明の概略のみを著述している)。また、ニュートンはその理論を月の運動に適用し三体問題の一般解を求めようとしたものの見出すことができず、プリンキピアでは近似解についてのみ記述している。
プリンキピアの第2巻は空気抵抗 などの抵抗力のもとでの物体の運動を扱っている。The System of the World と題された第3巻は前2巻とは異なり自然哲学 を扱ったもので、ニュートンはそれまでの巻で展開した数学理論を天界の物体の運動に適用した。木星の衛星、土星の衛星、そして惑星がいずれもケプラーの法則(第2法則と第3法則)を満たすことから、天体間には逆二乗則の引力が働いていること、そして地球-月間に働くこの引力は地球上の物体が地球の中心に向かって落下しようとする力(重力)と同じものであると論じている。そしてこのことからすべての物体間に重力が作用すること(万有引力の法則 )を主張した。さらに第3巻では自転する球体(すなわち地球)は扁平な形に変形すること、潮汐 が月の引力によるものであること、月の運動(ただしこの議論は成功しているとは言い難い)、月と太陽の重力による地球の歳差 の計算、彗星 の軌道といった内容が扱われている。
1693年にハレーは古代バビロニア および中世アラブ界の月食の記録を当時の記録と比較し、月の永年加速 を指摘した。1749年に en:Richard Dunthorne は永年加速の大きさを1平方世紀 あたり10秒 と求めた。
オイラーによって初めてニュートンの運動方程式は現代的な記法で書き下された。 ニュートンのプリンキピアは当時考案されたばかりの微分法 および積分法 の使用を避け幾何学的な考察に基づくものであり極めて難解なものであった。プリンキピアの出版後18世紀初頭にかけてピエール・ヴァリニョン (1654-1722)、ヨハン・ベルヌーイ (1667-1748)、Jakob Hermann (1678-1733) らはプリンキピアの内容をゴットフリート・ライプニッツ (1646-1716) らによる微積分学 の言葉を用いて理解するようになった。1730年頃からはダニエル・ベルヌーイ (1700-1782)、レオンハルト・オイラー (1707-1783)、アレクシス・クレロー (1713-1765)、ジャン・ル・ロン・ダランベール (1717-1783)らによって保存則やポテンシャルの概念などが導入され、1760年頃までには現在の力学に近い形にまで整備された。ダランベールは1743年に Traité de dynamique を出版した。オイラーは1749年にニュートンの運動方程式 を初めて現在知られている形で書き下している[ 210] ジョゼフ=ルイ・ラグランジュ (1736-1813) は1750年代から統一的な原理に基づく力学の再構築に取り組み、現在解析力学 (特にラグランジュ力学 )として知られる体系を1788年の著書 Mécanique analytique (英語版 )
上述のように、アイザック・ニュートンはプリンキピアにおいて惑星軌道が円錐曲線であるならば逆二乗則に従う中心力が作用していることを示したものの、逆に逆二乗則の重力を受けて運動する物体の軌道がどのようなものかという問題に対しては十分な回答を著述しなかった。この問題は1710年の Jakob Hermann の研究[ 214] [ 215] [ 216] [ 217]
1730年代にピエール・ルイ・モーペルテュイ (1698-1759) 率いる観測隊は地球が赤道 付近で膨らんでいる扁球 であることを証明した(フランス科学アカデミーによる測地遠征 )。これにより地球の形状に関するジャック・カッシーニ (1677-1756) の測量[ 220] アレクシス・クレロー は地球の形状に関する1743年の著書 Théorie de la figure de la terre を出版した後に天体力学の研究を始め、1747年11月にパリ で三体問題 に関する口頭発表を行い、月の近地点移動 を説明するためには万有引力の法則に逆三乗則に従う付加項が必要であると主張した(逆二乗則に補正を加えるというアイデアは John Keill にまで遡る)。この主張は激しい拒否反応を引き起こし、短距離側ではなく遠距離側で万有引力の法則を修正する必要があると考えていたレオンハルト・オイラーとの間で論戦となった。ダランベールもこの問題に興味を示し、独自のアイデアで研究に参入した。1714年に英国が定めた経度法 の懸賞金に繋がる可能性から月の近地点移動はこの三者による研究競争となったものの、1749年にクレローは当初の主張を撤回し当時は無視されていた太陽による高次摂動を考慮することによって月の近地点移動を説明できることを示し、この成果によって帝国サンクトペテルブルク科学アカデミー の賞を1750年に獲得した(受賞論文 Théorie de la lune は1753年に出版された)。その後クレローはハレー彗星 の軌道の摂動計算などの研究を行っている[ 229]
1748年にパリの科学アカデミー は木星と土星の相互摂動に関するコンテストを開催し、レオンハルト・オイラーが優勝した(受賞論文は1749年に出版された)。彼は木星と土星の運動のケプラー軌道からの逸脱を完全に説明することはできなかったものの、その後の天体力学の研究において極めて重要な役割を果たす三角級数 の方法を導入した。またオイラーの研究には観測データからのパラメータ推定に関する先駆的な業績が含まれている(当時最小二乗法 は考案されていなかった)。
トビアス・マイヤー (1723-1762) はオイラーの木星と土星の理論を発展させ太陽-地球-月系に応用することにより、月の天文表を作成し1753年に出版した。その正確さは1760年までにジェームズ・ブラッドリー (1693-1762) の観測によって裏付けられ、1767年に創刊された航海年鑑 の基礎となった。
ラグランジュ点。 レオンハルト・オイラーは三体問題を求積するために運動の積分 を探し求めたものの、必要な数の積分を得ることはできなかった。そこで三体が同一直線に乗る配位の特殊解に目を向け、1766年に三体問題に関する論文 Considerationes de motu corporum coelestium の中で制限三体問題の平衡点であるラグランジュ点 のうち直線解と呼ばれる L1 , L2 を発見した。ラグランジュは1772年にすべての平衡点、特に正三角形解を発見した[ 236]
円制限三体問題におけるヤコビ積分 (英語版 ) カール・グスタフ・ヤコブ・ヤコビ (1804-1851) によって導入された[ 237]
摂動論の基本的な道具立てはジョゼフ=ルイ・ラグランジュによって整備され、ピエール=シモン・ラプラス (1749-1827) によって発展した。接触軌道要素はレオンハルト・オイラーによって厳密に定義された。ラグランジュは月の秤動 に関する研究を行い、1764年にフランス科学アカデミーの賞を獲得した[ 239]
ピエール=シモン・ラプラスは1773年頃から天体力学の研究を始め、天体の運動および地球の形状・海の潮汐に取り組んだ。ラプラスは1776年に永年摂動の1次の範囲では惑星の軌道長半径は時間変化しないことを示した。また1787年に木星および金星の摂動によって地球軌道の離心率が変化することにより月の永年加速が説明できると主張した(なお半世紀以上が経った1854年にアダムズがラプラスの計算に誤りを発見し、この効果は観測を説明するのに必要な値の半分しかないことを指摘している)。1789年のフランス革命 に伴う環境の激変もありながら、ラプラスは1796年に Exposition du système du monde を、1799年から1827年にかけて5巻からなる『天体力学論 (英語版 ) [ 244] Traité de mécanique céleste ) を出版した。この著作は以下の内容を取り扱っている。
第1巻: (Book 1) 平衡と運動に関する一般論、(Book 2) 重力と物体の運動。
第2巻: (Book 3) 天体の形状、(Book 4) 海洋と大気の運動、(Book 5) 天体の重心まわりの運動。
第3巻: (Book 6) 惑星の運動、(Book 7) 月の運動。
第4巻: (Book 8) 木星、土星、天王星の衛星、(Book 9) 彗星、(Book 10) 世界観について。
第5巻: (Book 11) 地球の自転と形状、(Book 12) 弾性流体の運動、(Book 13) 惑星を覆う流体運動、(Book 14) 歳差と秤動、(Book 15) 惑星と彗星の運動、(Book 16) 衛星の運動 ラグランジュは1814年に出版した Mécanique analytique の第2版の中で摂動関数 およびラグランジュの惑星方程式 といった天体力学の基本的な道具立てをまとめ、高次摂動の系統的な計算が可能であることを示した。
ティティウス・ボーデの法則 は1766年にヨハン・ティティウス (1729-1796) によって発見され、1772年にヨハン・ボーデ (1747-1826) によって紹介されたことで知られるようになった[ 249]
a
n
=
0.4
+
0.3
×
2
n
A
U
(
n
=
−
∞
,
0
,
1
,
2
,
4
,
5
)
{\displaystyle a_{n}=0.4+0.3\times 2^{n}\,\mathrm {AU} \ \ (n=-\infty ,0,1,2,4,5)}
により与えらえるというものである。1781年のウィリアム・ハーシェル (1738-1822) による天王星 の発見が
n
=
6
{\displaystyle n=6}
[ 250]
ピアッツィによるケレスの観測データ。 1801年1月にジュゼッペ・ピアッツィ (1746-1826) は
n
=
3
{\displaystyle n=3}
ケレス を発見し(これは最初の小惑星 の発見であった)2月上旬まで観測を続けたものの、見失った[ 250] カール・フリードリヒ・ガウス (1777-1855) は同年9月からケレスの軌道計算に取り組み、11月にケレスの軌道計算に成功した。ガウスはフランツ・フォン・ツァハ (1754-1832) へ計算結果を送り、ツァハとヴィルヘルム・オルバース (1758-1840) はガウスの予測通りの位置にケレスを再発見した。さらに翌年に発見された小惑星パラス の軌道計算にも成功し、ガウスはゲッティンゲン大学 の天文台のポストを得た。ガウスはさらに天体力学の研究を進め、その成果を1809年に『天体運行論 』[ 253] [ 254] 羅 : Theoria motus corporum coelestium in sectionibus conicis solem ambientum ガウスの方法 (英語版 )
ウィリアム・ローワン・ハミルトン (1805-1865) は自身の光学 に関する研究から着想を得て1834年から35年にかけての一連の論文[ 259] [ 260] [ 261] ハミルトン力学 を創始した。1836年に円制限三体問題に新しい運動の積分を発見したヤコビはこの論文を書き上げた後にハミルトンの論文を読んだと考えられており、彼は力が時間に依存する場合へとハミルトンの理論を拡張し1837年に現在ハミルトン–ヤコビ方程式 として知られる単一の偏微分方程式を書き下した。ハミルトンの方程式 はヤコビによって「正準」 (仏 : canonique ) と命名された。
1821年にアレクシス・ブヴァール (1767-1843) は天王星の天文表を出版したが、その後の観測はブヴァールの計算と食い違った[ 266] ジョン・クーチ・アダムズ (1819-1892) とユルバン・ルヴェリエ (1811-1877) は独立にこの未知の惑星の軌道を計算し、ルヴェリエの予測をもとにヨハン・ゴットフリート・ガレ (1812-1910) が1846年に海王星 を発見した[ 266] ジェームズ・チャリス (1803-1882) とジョージ・ビドル・エアリー (1801-1892) も探索を試み、ガレによる発見の後に海王星を見出したが彼らは発見者とは認められていない[ 267]
1833年にシメオン・ドニ・ポアソン (1781-1840) は独立変数として真近点角
f
{\displaystyle f}
t
{\displaystyle t}
Philippe Gustave le Doulcet はこの方法を発展させた。
ルヴェリエは摂動関数の7次までの literal expansion を遂行し、1855年に出版した[ 269] [ 271] サイモン・ニューカム (1835-1909) らはさらに理論を発展させた。ペーター・ハンゼン (1795-1874) も摂動論に多くの貢献を行った。
1856年にジェームズ・クラーク・マクスウェル (1831-1879) は土星 の環 が固体であるならば不安定であることを証明し、無数の粒子からできているであろうことを指摘した。
1889年にフェリックス・ティスラン (1845-1896) は彗星の同一性に関するティスランの判定式 を提案した[ 274] 仏 : Traité de mécanique céleste [ 276]
シャルル=ウジェーヌ・ドロネー (1816-1872) は1860年および1867年に二巻からなる La Théorie du mouvement de la lune を出版し、月の運動について論じた。その中でドロネーは Jacques Binet (1786-1856) が1841年に導入した変数[ 278] ドロネー変数 として知られる正準変数を定義している。ただしドロネーの理論は級数の収束が遅く十分な精度を得るためには多大な計算を要するという難点があった。
ジョージ・ウィリアム・ヒル (1838-1914) は1870年代からドロネーの理論を発展させた。彼は月の軌道を楕円軌道ではなく三体問題の近似解である卵形の軌道として扱い、またそれまで天体力学ではあまり普及していなかった複素指数関数
e
±
−
1
θ
=
cos
θ
±
−
1
sin
θ
{\displaystyle e^{\pm {\sqrt {-1}}\theta }=\cos \theta \pm {\sqrt {-1}}\sin \theta }
を全面的に採用した。アーネスト・ウィリアム・ブラウン (1866-1938) は1896年に An Introductory Treatise on the Lunar Theory を出版した[ 283]
19世紀末に三体問題の求積不可能性が Heinrich Bruns (1848-1919) によるブルンスの定理 、そしてアンリ・ポアンカレ (1854-1912) によるポアンカレの定理 によって明らかになった。ポアンカレはこの定理および関連する彼の研究成果を1892年から1899年にかけて出版された3巻からなる著書『天体力学の新しい方法』 (仏 : Les méthodes nouvelles de la mécanique céleste 力学系 の理論を創始した。なお、先行する1880年代にはアレクサンドル・リャプノフ (1857-1918) が力学系の先駆的な研究を行っている。ポアンカレの力学系の理論はジョージ・デビット・バーコフ (1884-1944) らによって受け継がれ20世紀に大きく発展した。バーコフは1927年に Dynamical Systems を出版している。
20世紀に入ってからもエードヴァルド・ヒューゴ・フォン・ツァイペル (英語版 ) [ 292] Anders Lindstedt )-ポアンカレの方法を発展させた[ 293] トゥーリオ・レヴィ=チヴィタ (1873-1941)、カール・スンドマン (1873-1949) らは三体問題の数学的な研究を継続した。
アルベルト・アインシュタイン (1879-1955) は1915年に一般相対性理論 を完成させた。この理論は強重力場中でニュートン理論への補正項を生じ、アインシュタインはこれによって水星 の近日点移動 の予測値と観測値の不一致(これはルヴェリエによって発見された)が説明できることを示した。後に5巻からなる Celestial mechanics を出版したことで知られる萩原雄祐 (1897-1979) は1930年代に一般相対論的天体力学の研究を行った[ 299] [ 300] レオポルト・インフェルト 、バーネッシュ・ホフマン とともにポスト・ニュートン展開 による補正項を含むN体系の運動方程式であるアインシュタイン・インフェルト・ホフマンの方程式 (英語版 ) [ 301] [ 302]
20世紀には観測技術の進展によって太陽系天体が多く発見され、またその理論も進展した。平山清次 (1874-1943) は1918年に小惑星の族の概念を導入した[ 303] クライド・トンボー (1906-1997) は1930年に冥王星 を発見した(冥王星は2006年のIAU決議によって惑星から準惑星へと分類が変更された)[ 304] Mikhail Lidov (1926-1993) と古在由秀 (1928-2018) は1961年から62年に彗星が大きな離心率を獲得する機構を説明し得る古在メカニズム を提案した[ 305] [ 306] ピーター・ゴールドレイク (1939-) とScott Tremaine (1950-) は1979年に環における羊飼い衛星 の存在を理論的に予想した[ 307]
ソ連のスプートニク計画 による1957年に世界初の人工衛星スプートニク1号 の打ち上げ以降、宇宙空間における人工物の軌道制御を扱う軌道力学 が急速に進展した。また同時期に電子計算機が実用化されたことにより数値シミュレーションによる軌道計算が可能となった。一方で理論的研究も続けられ、アンドレイ・コルモゴロフ (1903-1987) らによるKAM理論 、堀源一郎 (1930-) らによるリー変換摂動論 [ 309] 吉田春夫 らによるシンプレクティック数値積分法 、そして杉本大一郎 らによるGRAPE などの特筆に値する発展がある。
理科年表2021年版[ 311]
太陽系惑星の軌道要素
惑星
質量 [
M
⊙
{\displaystyle M_{\odot }}
軌道長半径
a
{\displaystyle a}
離心率
e
{\displaystyle e}
軌道傾斜角
i
{\displaystyle i}
軌道傾斜角
i
{\displaystyle i}
近日点黄経
ϖ
{\displaystyle \varpi }
昇交点黄経
Ω
{\displaystyle \Omega }
元期平均近点角
M
0
{\displaystyle M_{0}}
水星
1.6601×10-7
0.3871
0.2056
7.004
6.343
77.490
48.304
282.128
金星
2.4478×10-6
0.7233
0.0068
3.394
2.196
131.565
76.620
35.951
地球
3.0404×10-6
1.0000
0.0167
0.003
1.578
103.007
174.821
179.912
火星
3.2272×10-7
1.5237
0.0934
1.848
1.680
336.156
49.495
175.817
木星
9.5479×10-4
5.2026
0.0485
1.303
0.328
14.378
100.502
312.697
土星
2.8589×10-4
9.5549
0.0555
2.489
0.934
93.179
113.610
219.741
天王星
4.3662×10-5
19.2184
0.0464
0.773
1.028
173.024
74.022
233.182
海王星
5.1514×10-5
30.1104
0.0095
1.770
0.726
48.127
131.783
303.212
国立天文台による月の平均軌道要素(J2000.0の平均春分点および黄道による)[ 312]
T
{\displaystyle T}
J
{\displaystyle J}
T
=
(
J
−
2451545
)
/
36525
{\displaystyle T=(J-2451545)/36525}
[ 313]
a
=
383397.7725
+
0.0040
T
[
k
m
]
{\displaystyle a=383397.7725+0.0040T\,[\mathrm {km} ]}
e
=
0.055545526
−
0.000000016
T
{\displaystyle e=0.055545526-0.000000016T}
λ
=
218.31664563
∘
+
1732559343.48470
″
T
−
6.3910
″
T
2
+
0.006588
″
T
3
−
0.00003169
″
T
4
{\displaystyle \lambda =218.31664563^{\circ }+1732559343.48470''T-6.3910''T^{2}+0.006588''T^{3}-0.00003169''T^{4}}
ϖ
=
83.35324312
∘
+
14643420.2669
″
T
−
38.2702
″
T
2
−
0.045047
″
T
3
+
0.00021301
″
T
4
{\displaystyle \varpi =83.35324312^{\circ }+14643420.2669''T-38.2702''T^{2}-0.045047''T^{3}+0.00021301''T^{4}}
i
=
5.15668983
∘
−
0.00008
″
T
+
0.02966
″
T
2
−
0.000042
″
T
3
−
0.00000013
″
T
4
{\displaystyle i=5.15668983^{\circ }-0.00008''T+0.02966''T^{2}-0.000042''T^{3}-0.00000013''T^{4}}
Ω
=
125.04455501
∘
−
6967919.3631
″
T
+
6.3602
″
T
2
+
0.007625
″
T
3
−
0.00003586
″
T
4
{\displaystyle \Omega =125.04455501^{\circ }-6967919.3631''T+6.3602''T^{2}+0.007625''T^{3}-0.00003586''T^{4}}
^ 二体間に働く万有引力の大きさは二体の質量の積に比例する。 しかし一方の天体(中心天体)を原点とする座標系(相対座標)では、運動方程式の右辺に現れる項は質量の和に比例する。二体問題 も参照。
^ 「天体力学 」 - 日本天文学会 編『天文学辞典』
^ ヨアヒム・ヘルマン (ドイツ語版 ) 小平桂一 監修 『カラー天文百科』 平凡社 、1976年 3月25日 初版第1刷発行、18-19頁^ 「ケプラー運動 」 - 日本天文学会 編『天文学辞典』
^ 「ケプラーの法則 」 - 日本天文学会 編『天文学辞典』
^ 「近点 」 - 日本天文学会 編『天文学辞典』
^ 「近日点 」 - 日本天文学会 編『天文学辞典』
^ 「近地点 」 - 日本天文学会 編『天文学辞典』
^ 「遠点 」 - 日本天文学会 編『天文学辞典』
^ a b 「離心近点角 」 - 日本天文学会 編『天文学辞典』
^ 「軌道要素 」 - 日本天文学会 編『天文学辞典』
^ a b c 「近日点引数 」 - 日本天文学会 編『天文学辞典』
^ a b 「軌道傾斜角 」 - 日本天文学会 編『天文学辞典』
^ a b c 「昇交点 」 - 日本天文学会 編『天文学辞典』
^ 「黄道座標系 」 - 日本天文学会 編『天文学辞典』
^ 古在由秀. “天体力学の話 ” (PDF). 2021年2月16日 閲覧。 ^ “星の軌道計算について ” (PDF). 2021年2月16日 閲覧。 ^ 長沢工『軌道決定の原理 彗星・小惑星の観測方向から距離を求めるには』地人書館、2003年。ISBN 978-4805207314 。 ^ a b 「摂動 」 - 日本天文学会 編『天文学辞典』
^ 「接触軌道要素 」 - 日本天文学会 編『天文学辞典』
^ a b Mardling, Rosemary A. (2013). “New developments for modern celestial mechanics – I. General coplanar three-body systems. Application to exoplanets”. Monthly Notices of the Royal Astronomical Society 435 (3): 2187–2226. doi :10.1093/mnras/stt1438 . ISSN 1365-2966 .
^ 「永年摂動 」 - 日本天文学会 編『天文学辞典』
^ Goldstein, Herbert; Poole, Charles; Safko, John (2001). Classical Mechanics (third ed.). Pearson. p. 477. ISBN 978-0201657029 ^ “暦Wiki/太陰暦 ”. 国立天文台暦計算室. 2021年2月16日 閲覧。 ^ 岡村定矩 池内了 海部宣男 佐藤勝彦 永原裕子, ed (2017). シリーズ現代の天文学 1 人類の住む宇宙 第2版 . 日本評論社. pp. 349-351. ISBN 9784535607514 ^ a b c d e “暦Wiki/月の公転運動 ”. 国立天文台暦計算室. 2021年2月13日 閲覧。
^ a b “太陰運動論とは - コトバンク ”. 2021年3月19日 閲覧。
^ “月運動論とは - コトバンク ”. 2021年3月19日 閲覧。 ^ 「尽数関係 」 - 日本天文学会 編『天文学辞典』
^ 「平均運動共鳴" 」 - 日本天文学会 編『天文学辞典』
^ 「カークウッドの間隙 」 - 日本天文学会 編『天文学辞典』
^ 「共鳴外縁天体 」 - 日本天文学会 編『天文学辞典』
^ Barnes, Rory (2011). “Laplace Resonance”. Encyclopedia of Astrobiology (Springer): 905–906. doi :10.1007/978-3-642-11274-4_864 . ^ a b 「永年共鳴" 」 - 日本天文学会 編『天文学辞典』
^ “Opticks by Isaac Newton ”. Project Gutenberg. 2021年2月15日 閲覧。 ^ Eckert, W. J.; Brouwer, D.; Clemence, G. M. (1951). “Coordinates of the Five Outer Planets 1653-2060” . Astron. Pap. Amer. Ephemeris. Naut. Alm. 12 . https://books.google.co.jp/books?id=TVMnAQAAIAAJ . ^ Laskar, J. (1989). “A numerical experiment on the chaotic behaviour of the Solar System”. Nature 338 (6212): 237–238. doi :10.1038/338237a0 . ISSN 0028-0836 . ^ Ito, Takashi; Tanikawa, Kiyotaka (2002). “Long-term integrations and stability of planetary orbits in our Solar system”. Monthly Notices of the Royal Astronomical Society 336 (2): 483–500. doi :10.1046/j.1365-8711.2002.05765.x . ISSN 1365-2966 . ^ 伊藤孝士. “太陽系惑星運動の安定性 ” (PDF). 2021年2月14日 閲覧。 ^ Kinoshita, Hiroshi (1977). “Theory of the rotation of the rigid earth”. Celestial Mechanics 15 (3): 277–326. doi :10.1007/BF01228425 . ISSN 0008-8714 . ^ 「潮汐力 」 - 日本天文学会 編『天文学辞典』
^ a b c 「潮汐 」 - 日本天文学会 編『天文学辞典』
^ 「潮汐加熱 」 - 日本天文学会 編『天文学辞典』
^ a b 「潮汐摩擦 」 - 日本天文学会 編『天文学辞典』
^ “暦Wiki/潮汐/潮汐摩擦 ”. 国立天文台暦計算室. 2021年2月14日 閲覧。 ^ 「潮汐ロック 」 - 日本天文学会 編『天文学辞典』
^ 大貫義郎 、吉田春夫『岩波講座 現代の物理学〈1〉力学』(第2刷)岩波書店、1997年、162-170頁。ISBN 4-00-010431-4 。 ^ 「ラグランジュ点 」 - 日本天文学会 編『天文学辞典』
^ 「羊飼い衛星 」 - 日本天文学会 編『天文学辞典』
^ a b Shevchenko, Ivan I. (2017). “The Lidov-Kozai Effect - Applications in Exoplanet Research and Dynamical Astronomy”. Astrophysics and Space Science Library . 441 . Cham: Springer International Publishing. pp. 105-115. doi :10.1007/978-3-319-43522-0 . ISBN 978-3-319-43520-6 . ISSN 0067-0057
^ a b Tsiganis, K. (2007). Benest D., Froeschle C., Lega E.. ed. “Chaotic Diffusion of Asteroids”. Topics in Gravitational Dynamics (Springer): 111. doi :10.1007/978-3-540-72984-6_5 .
^ 「ポインティング-ロバートソン効果 」 - 日本天文学会 編『天文学辞典』
^ 久保岡 俊宏. “やさしい軌道力学 - 人工衛星に作用する摂動 - ” (PDF). pp. 19-20. 2021年2月15日 閲覧。 ^ Merritt, David (2013). Dynamics and Evolution of Galactic Nuclei ISBN 9781400846122 . https://openlibrary.org/works/OL16802359W/Dynamics_and_Evolution_of_Galactic_Nuclei ^ 「パルサー連星 」 - 日本天文学会 編『天文学辞典』
^ Maggiore, Michele (2007). Gravitational Waves: Theory and Experiments . Oxford University Press. pp. 184-189. ISBN 978-0198570745 ^ a b Binney, James; Tremaine, Scott (2008). Galactic Dynamics (Second ed.). Princeton University Press. p. 1. ISBN 978-0-691-13027-9
^ ヨハネス・ケプラー 著、岸本良彦 訳『新天文学』工作舎、2013年。ISBN 978-4875024538 。 ^ ヨハネス・ケプラー 岸本良彦訳 (2009). 宇宙の調和 . 工作舎. ISBN 978-4875024187 ^ Euler, Leonhard (1749). “Recherches sur le mouvement des corps célestes en général” . Mémoires de l'académie des sciences de Berlin 3 : 93-143. https://scholarlycommons.pacific.edu/euler-works/112/ . ^ Hermann, Jacob (1710). “Extrait d’une Lettre de M. Herman à M. Bernoulli, datée de Padoüe le 12. Juillet 1710”. Mémoires de l’Académie des Sciences : 519–521. ^ Bernoulli, Johann (1710). “Extrait de la Réponse de M. Bernoulli à M. Herman, Datée de Basle le 7 Octobre 1710”. Mémoires de l’Académie des Sciences : 521–33. ^ Speiser, David (1996). “The Kepler Problem from Newton to Johann Bernoulli”. Archive for History of Exact Sciences 50 (2): 103–116. doi :10.1007/BF02327155 . ISSN 0003-9519 . ^ Guicciardini, Niccolò (2015). Proofs and Contexts: the Debate between Bernoulli and Newton on the Mathematics of Central Force Motion . pp. 67–102. doi :10.1007/978-3-319-12030-0_4 . ISSN 2297-2951 . ^ Cassini, J. (1720). De la grandeur et de la figure de la terre . https://books.google.fr/books?id=u0liAAAAcAAJ ^ Grier, David Alan (2005). “The First Anticipated Return: Halley's Comet 1758” . When Computers Were Human . Princeton: Princeton University Press . p. 16. ISBN 0-691-09157-9 . https://books.google.com/books?id=YTcDAQAAQBAJ&pg=PA11 ^ Lagrange, J.-L. (1772). “Essai sur le Problème des trois Corps”. Prix de l’Académie des Sciences de Paris . ^ C.G.J. Jacobi, Comptes rendus de l’Académie des Sciences de Paris , III, 5961.
^ Dirk Jan Struik (2021年2月14日). “Joseph-Louis Lagrange, comte de l'Empire - Encyclopedia Britannica ”. 2021年2月13日 閲覧。 ^ “『天体力学論』 ラプラス著 1799 ~1825年 ”. 2021年2月12日 閲覧。 ^ “Bode's law ”. Britanica. 2021年2月15日 閲覧。 ^ a b “Asteroid ”. Britanica. 2021年2月15日 閲覧。
^ 松本桂. “スティグラーの法則 ”. 2021年3月19日 閲覧。 ^ “知の系譜 ” (PDF). 広島経済大学図書館. p. 10. 2021年3月19日 閲覧。 ^ Hamilton, William R (1834). “On a General Method in Dynamics”. Philosophical Transactions of the Royal Society, part II : 247-308. ^ Hamilton, William R (1834). “On the Application to Dynamics of a General Mathematical Method Previously Applied to Optics”. Report of the British Association for the Advancement of Science : 513-518. ^ Hamilton, William R (1835). “Second Essay on a General Method in Dynamics”. Philosophical Transactions of the Royal Society, part I : 95-144. ^ a b “Neptune ”. 2021年2月15日 閲覧。
^ “Neptune’s discovery ”. Britanica. 2021年2月15日 閲覧。 ^ Le Verrier, U.-J.J. (1855). Ann. Obs. Paris, Mem. 1 : 258–331. ^ Boquet, Felix (1889). “Développement de la fonction perturbatrice : calcul des termes du huitième ordre”. Annales de l'Observatoire de Paris 19 : B1-B75. Bibcode : 1889AnPar..19B...1B . ^ F. Tisserand (1889). “Sur la théorie de la capture des comètes périodiques”. Bulletin Astronomique, Serie I 6 : 289-292. Bibcode : 1889BuAsI...6..289T . ^ “Traité de mécanique céleste ”. Britannica. 2021年3月19日 閲覧。 ^ Binet, Jacques (1841). “Mémoire sur la variation des constantes arbitraires dans les formules générales de la Dynamique et dans un système d'équations analogues plus étendues”. Journal de l'École Polytechnique 17 : 1-94. ^ Brown, E.W. (1896). An Introductory Treatise on the Lunar Theory . Cambridge University Press ^ F. ディアク、P. ホームズ 著、吉田春夫 訳『天体力学のパイオニアたち 上』シュプリンガー・フェアラーク東京、2004年、127頁。ISBN 4-431-71114-7 。 ^ H. von Zeipel, Ark. Astron. Mat. Phys., 11 , 12 , 13 (1916-17).
^ 「萩原雄祐 」 - 日本天文学会 編『天文学辞典』
^ Hagihara, Y. (1930). “Theory of the Relativistic Trajeetories in a Gravitational Field of Schwarzschild”. Japanese Journal of Astronomy and Geophysics 8 : 67. Bibcode : 1930JaJAG...8...67H . ^ Einstein, A.; Infeld, L.; Hoffmann, B. (1938). “The Gravitational Equations and the Problem of Motion”. Annals of Mathematics 39 (1): 65–100. Bibcode : 1938AnMat..39...65E . doi :10.2307/1968714 . JSTOR 1968714 . ^ Maggiore, Michele (2007). Gravitational Waves: Theory and Experiments . Oxford University Press. pp. 245-247. ISBN 978-0198570745 ^ 「族(小惑星の)" 」 - 日本天文学会 編『天文学辞典』
^ 「冥王星" 」 - 日本天文学会 編『天文学辞典』
^ Lidov, Mikhail L. (1961). “Эволюция орбит искусственных спутников под воздействием гравитационных возмущений внешних тел” (ロシア語). Iskusstvennye Sputniki Zemli 8 : 5–45. Lidov, Mikhail L. (1962). “The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies”. Planetary and Space Science 9 (10): 719–759. Bibcode : 1962P&SS....9..719L . doi :10.1016/0032-0633(62)90129-0 . ^ Kozai, Yoshihide (1962). “Secular perturbations of asteroids with high inclination and eccentricity”. Astronomical Journal 67 : 591. Bibcode : 1962AJ.....67..591K . doi :10.1086/108790 . ^ Goldreich, Peter; Tremaine, Scott (1979). “Towards a theory for the Uranian rings.” . Nature 277 (5692): 97–99. doi :10.1038/277097a0 . https://www.nature.com/articles/299209a0.pdf?origin=ppub . ^ 堀源一郎:Theory of general perturbations with unspecified canonical variables , Publ. Astron. Soc. Japan Vol.18, pp.287-296(1966) ^ 国立天文台 編『理科年表 2021』丸善出版、2020年11月。ISBN 978-4-621-30560-7 。 ^ “暦Wiki/平均軌道要素 ”. 国立天文台暦計算室. 2021年2月15日 閲覧。 ^ “暦Wiki/ユリウス世紀数 ”. 国立天文台暦計算室. 2021年2月15日 閲覧。
福島登志夫 編『シリーズ現代の天文学 13 天体の位置と運動』(第2版)日本評論社、2017年7月。ISBN 9784535607637 。 木下宙『天体と軌道の力学』東京大学出版会、1998年。ISBN 978-4-13-060721-6 。 Murray, Carl D.; Dermott, Stanley F. (2000). Solar System Dynamics . Cambridge University Press. doi :10.1017/CBO9781139174817 . ISBN 9780521575973 Brouwer, Dirk; Clemence, Gerald M. (1961). Methods of Celestial Mechanics . Academic Press. ISBN 9781483212357 Plummer, H. C. (1918). An Introductory Treatise on Dynamical Astronomy . https://archive.org/details/introductorytrea00plumuoft Boccaletti, Dino; Pucacco, Giuseppe (2004). Theory of Orbits: Volume 1: Integrable Systems and Non-perturbative Methods . Springer. doi :10.1007/978-3-662-03319-7 . ISBN 978-3-642-08210-8 Boccaletti, Dino; Pucacco, Giuseppe (2002). Theory of Orbits: Volume 2: Perturbative and Geometrical Methods . Springer. ISBN 3-540-60355-7 Beutler, Gerhard (2005a). Methods of Celestial Mechanics Volume I: Physical, Mathematical, and Numerical Principles . Springer. doi :10.1007/b138225 . ISBN 978-3-540-40749-2 Beutler, Gerhard (2005b). Methods of Celestial Mechanics Volume II: Application to Planetary System, Geodynamics and Satellite Geodesy . Springer. doi :10.1007/b137725 . ISBN 978-3-540-26512-2 Geiges, H. (2016). The Geometry of Celestial Mechanics . Cambridge University Press. doi :10.1017/CBO9781316410486.003 George W. Collins, II (2004). Foundations of Celestial Mechanics Bibcode : 1989fcm..book.....C . http://bifrost.cwru.edu/personal/collins/celest/
Timberlake, Todd; Wallace, Paul (2019). Finding our Place in the Solar System: The Scientific Story of the Copernican Revolution . Cambridge University Press. doi :10.1017/9781316856208 . ISBN 9781316856208 Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation . Freeman. ISBN 0-7167-0344-0 N.N. Bogolyubov, G.K. Mikhaĭlov, and A.P. Yushkevich, ed (2007). Euler and modern science . Mathematical Association of America Wilson, Curtis (2010). The Hill-Brown Theory of the Moon’s Motion: Its Coming-to-be and Short-lived Ascendancy (1877-1984) . Springer. doi :10.1007/978-1-4419-5937-9 . ISBN 978-1-4419-5937-9 Barrow-Green (1997). Poincaré and the Three-Body Problem . American Mathematical Society. doi :10.1090/hmath/011/01 Wepster, Steven (2010). Between Theory and Observations: Tobias Mayer's Explorations of Lunar Motion, 1751-1755 . Springer. doi :10.1007/978-1-4419-1314-2 . ISBN 978-1-4419-1314-2 I. Grattan-Guinness, Roger Cooke, Leo Corry, Pierre Crépel, Niccolo Guicciardini, ed (2005). Landmark Writings in Western Mathematics 1640-1940 . Elsevier. doi :10.1016/B978-0-444-50871-3.X5080-3 . ISBN 978-0-444-50871-3 Matthew S. Tiscareno & Carl D. Murray, ed (2018). Planetary Ring Systems: Properties, Structure, and Evolution . Cambridge University Press. doi :10.1017/9781316286791 . ISBN 9781316286791
伊藤孝士, 谷川清隆 (2007年). “21世紀の天体力学 ” (PDF). 2021年2月12日 閲覧。 谷川清隆「天体力学とハミルトン力学系 : 「現象と応用」 (近可積分ハミルトン系の数理と応用) 」『数理解析研究所講究録』第1282巻、京都大学数理解析研究所、2002年9月、4-16頁、CRID 1050001335517748224 、hdl :2433/42389 ISSN 1880-2818 、2023年12月21日 閲覧 中根美知代 (1999年). “Hamilton-Jacobi理論の新展開 Poincaréによる「Jacobiの定理」の解釈 ” (PDF). 2021年2月14日 閲覧。 Wilson, Curtis (1985). “The great inequality of Jupiter and Saturn: from Kepler to Laplace”. Archive for History of Exact Sciences 33 (1-3): 15–290. doi :10.1007/BF00328048 . ISSN 0003-9519 . Bodenmann, Siegfried (2010). “The 18th-century battle over lunar motion” . Physics Today 63 (1): 27–32. Bibcode : 2010PhT....63a..27B . doi :10.1063/1.3293410 . ISSN 0031-9228 . http://sites.apam.columbia.edu/courses/ap1601y/Lunar_Motion_PhysToday_2010.pdf . Terrall, Mary (1992). “Representing the Earth's Shape: The Polemics Surrounding Maupertuis's Expedition to Lapland” . Isis 83 (2): 218-37. http://www.jstor.org/stable/234505 . Caparrini, Sandro (2014). “The history of the Méchanique analitique”. Lettera Matematica 2 (1-2): 47–54. doi :10.1007/s40329-014-0043-3 . ISSN 2281-6917 . Nakane, Michiyo; Fraser, Craig G. (2002). “The Early History of Hamilton-Jacobi Dynamics 1834-1837”. Centaurus 44 (3-4): 161–227. doi :10.1111/j.1600-0498.2002.tb00613.x . ISSN 0008-8994 . Kushner, D. (1989). “The controversy surrounding the secular acceleration of the moon's mean motion”. Archive for History of Exact Sciences 39 : 291-316. Bibcode : 1989AHES...39..291K . doi :10.1007/BF00348444 . Peale, Stanton J. (2015). “Celestial mechanics” . Encyclopedia Britannica . https://www.britannica.com/science/celestial-mechanics-physics . Laskar, J. (2013). Duplantier B., Nonnenmacher S., Rivasseau V.. ed. “Is the Solar System Stable?”. Chaos. Progress in Mathematical Physics (Basel: Birkhäuser) 66 . doi :10.1007/978-3-0348-0697-8_7 .
ウィキメディア・コモンズには、
天体力学 に関連するメディアがあります。
主要項目 観測手段 主な光学望遠鏡 人物 天体 学会 関連項目





















































![{\displaystyle \sum _{k=1}^{6}[\sigma _{j},\sigma _{k}]{\frac {d\sigma _{k}}{dt}}={\frac {\partial R}{\partial \sigma _{j}}}\ \ (j=1,2,\ldots ,6)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22fbc72dfb2f5eb5c4761829344c8eafceeace76)
![{\displaystyle [c_{j},c_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d8778477fba7c1ffa13569cc32d79d38ddd341)


![{\displaystyle {\frac {de}{dt}}=-{\frac {\sqrt {1-e^{2}}}{na^{2}e}}[1-{\sqrt {1-e^{2}}}]{\frac {\partial R}{\partial \epsilon }}-{\frac {\sqrt {1-e^{2}}}{na^{2}e}}{\frac {\partial R}{\partial \varpi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f5737793831d546a8454719c95aed2f6e42928f)

![{\displaystyle {\frac {d\epsilon }{dt}}=-{\frac {2}{na}}{\frac {\partial R}{\partial a}}+{\frac {\sqrt {1-e^{2}}}{na^{2}e}}[1-{\sqrt {1-e^{2}}}]{\frac {\partial R}{\partial e}}+{\frac {\tan(i/2)}{na^{2}{\sqrt {1-e^{2}}}}}{\frac {\partial R}{\partial i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/054059e33a87c680db286467ced7a03b3ae883a2)



































































![{\displaystyle a=383397.7725+0.0040T\,[\mathrm {km} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49050437740662005cc06f80b80d6ea95902798d)




