|
軌道共鳴
軌道共鳴(きどうきょうめい、orbital resonance[1])とは、天体力学において、ある天体の周りを公転する2つの天体が互いに重力を及ぼし合う結果、両者の軌道が変化すること[1]。公転周期と同程度の短い時間スケールで影響する平均運動共鳴[2]と、104 - 106 年の長い時間スケールで影響する永年共鳴[3]がある。 歴史17世紀にニュートンの運動の法則が発見されて以来、惑星軌道の安定性の問題はピエール=シモン・ラプラスを始めとして多くの数学者を虜にしてきた。太陽系の惑星の軌道は太陽とその周囲を公転する1惑星という2体問題近似の下では安定な軌道をとるが、この近似では他の天体の影響は無視している。これに他の惑星との相互作用を加えると、たとえそれが非常に微小な摂動であっても、長い時間にわたって影響を与え続け、最終的には惑星の軌道要素を変化させて太陽系の惑星は全く異なる配置になるはずである。しかし実際にはそのようなことは起きていない[注 1]ことから、惑星の軌道を安定化させる何か別のメカニズムが存在すると考えられた。この問題の解答を最初に発見したのはラプラスで、彼はガリレオ衛星の運動に見られる変わった振動の原因をこの共鳴理論で説明した。なおその後、擾乱の存在にもかかわらず天体が長期的に安定した軌道を維持できることはKAM定理により説明づけられた。ラプラス以降、軌道共鳴の研究は今日に至るまで活発に行なわれており、現在でも未解明の問題が数多く残されている。例として、巨大惑星の環の粒子と衛星とが相互作用して環の形状を維持する機構などはいまだに解明されていない。 太陽系の惑星や衛星に尽数関係が頻繁に見られることは古くから認識されており、1954年のRoyとOvendenの研究は、太陽系における尽数関係の現出頻度が単なる偶然では説明できないほどに高いことを統計的に実証し、太陽系の形成過程で尽数関係を生み出す何らかの物理機構が存在していたであろうということを示唆した[4]。 共鳴の種類軌道共鳴は一般に以下のような性質を持つ。
平均運動共鳴平均運動共鳴[2](へいきんうんどうきょうめい、mean motion resonance[2])とは、中心天体の周りを公転する2つの天体の公転周期の比が1:2や2:3など簡単な整数比(尽数関係、commensurability)となっている状態のこと。ここでいう「平均運動」(mean motion) とは、中心天体の重力を受けて楕円軌道を描く天体の、一周期で平均した公転角速度のことである[2]。 平均運動共鳴の結果、軌道が安定化することも不安定化することもある。共鳴の結果、2つの天体が近接遭遇を起こさないような配置となった場合は軌道が安定化する[2]。例として以下のようなケースがある。
小さな天体の場合は共鳴によって軌道が不安定化する場合の方が多い。例として以下のようなケースがある。
3個またはそれ以上の天体の公転周期が互いに簡単な整数比になっている場合の共鳴をラプラス共鳴 (Laplace resonance) と呼ぶ。例えば、木星の衛星ガニメデ・エウロパ・イオの三つは互いに 1:2:4 の軌道共鳴の状態にある。 永年共鳴永年共鳴 (secular resonance) [3][5]は、公転周期よりも長い時間スケールで小天体の軌道を不安定化させる共鳴である。複数の惑星が公転している系では、惑星同士の重力相互作用によって惑星軌道の近日点経度は徐々に回転し(近日点歳差)、軌道離心率の振動、昇交点経度の回転、軌道傾斜角の振動等の変化も起きる[1]。これらの変化は周期が104 - 106年と非常に長い時間スケールに及ぶことから永年摂動と呼ばれる。惑星小天体の近日点経度または昇降点経度の移動速度が等しくなると、惑星からの重力作用が小天体の軌道離心率や軌道傾斜角に与える影響が非常に大きくなるため、軌道が不安定となる。このような共鳴関係を永年共鳴と呼ぶ。 太陽系の場合、近日点経度に関する永年共鳴では、ギリシャ文字 ν に対応する惑星の番号を太陽に近い順に1から8までの添字としてつけて表記する[3]。昇降点経度に関する共鳴では、同じくギリシャ文字 ν に1と惑星の番号を用いて表記する。永年共鳴は小惑星や太陽系外縁天体の軌道進化、惑星形成過程に影響を及ぼしたと考えられている[5]。 顕著な例として以下のものがある。
太陽系の平均運動共鳴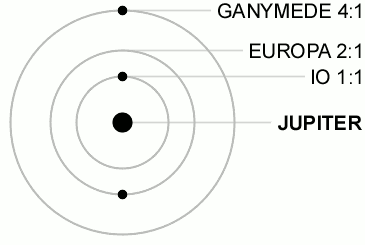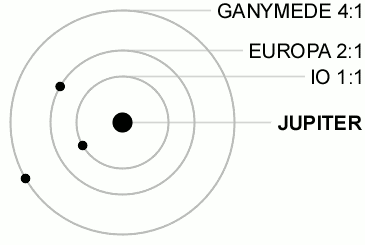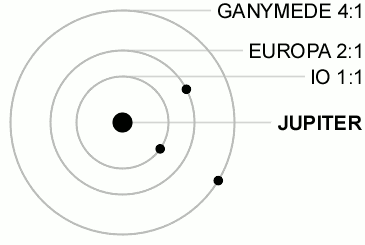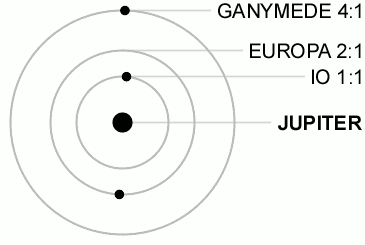 太陽系の惑星や衛星の間には次の5つの平均運動共鳴のみが知られている。(より大きな整数比の共鳴は小惑星や惑星の環、小衛星などにのみ見られる。)
公転周期の整数比は共鳴の性質を簡潔に表す便利なものだが、実際には以下のようなより複雑な関係が存在している。 後者の例としてよく知られたイオとエウロパの 1:2 共鳴を考える。公転周期がこのような整数比になっていると、平均運動 (公転周期の逆数の次元を持ち、度/日の単位で表されることが多い)は次の関係を満たす。
しかし実際にイオとエウロパの平均運動の値を上式の左辺に代入してみると、結果は -0.7395 °/日となって 0 にならない。 実際には共鳴自体は完全だが、ここに近木点(木星に最も近い点)の歳差が加わる。よって正しい式は以下のようになる(これはラプラス方程式の一部となっている)。
すなわち、イオの平均運動は近木点の歳差を考慮に入れればエウロパの平均運動のちょうど2倍になる。もし移動する近木点からこれらの天体を観測すると、この二つの衛星は(近木点からの離角が)常に同じ位置で会合を迎えるのを見ることになる。上に挙げた他の平均運動共鳴の例でも同様の関係を満たしている。ただしミマスとテティスの場合は例外で、下記の式を満たす。
この場合、会合点は両衛星の交点の中点を中心として振動する。 ラプラス共鳴イオ-エウロパ-ガニメデの間に見られる最も注目すべき軌道共鳴では、以下の関係によって衛星同士の軌道上の位相が同期している。
ここで は衛星の平均黄経である。この関係があるため、この系では3個の衛星の三重会合は決して起こらない。 「準」平均運動共鳴太陽系の衛星の中には以下のような共鳴に近い関係のものも存在する。 土星系: 天王星系: 土星系や木星系に共鳴が存在するにもかかわらず天王星系に(完全な)共鳴が見られない理由は分かっていない。 また、海王星‐冥王星以外の惑星の公転周期についても以下のような準共鳴状態が存在していると主張する者もいる。
(ティティウス・ボーデの法則を参照のこと)しかし、様々な研究が行なわれているにもかかわらず、これらの準尽数関係については有力な証拠は得られていない。 太陽系外惑星の軌道共鳴惑星同士の軌道共鳴関係は、太陽系外の惑星系で多数発見されている。3個以上の惑星が共鳴関係を成している例も発見されており、例えばグリーゼ876では、3つの惑星が、木星のガリレオ衛星と同様に1:2:4の公転周期で公転している。 大質量(木星質量以上)の惑星では、2:1の平均運動共鳴にあるペアが多く見出されている。このような共鳴関係は、惑星形成の過程で、隣接する惑星が惑星移動(軌道半径の変化)を起こした場合に生じるとされる[7]。一方、低質量の系外惑星でも共鳴は発見されているが、大質量惑星と比べてその頻度が低いことがケプラー宇宙望遠鏡の観測により判明している[7]。 注釈
出典
参考文献
関連項目外部リンク
|
|||||||||||||||||||||





