Integer number 6
Natural number
6 (six ) is the natural number following 5 and preceding 7 . It is a composite number and the smallest perfect number .[ 1]
In mathematics
A six-sided polygon is a hexagon ,[ 1] regular polygons capable of tiling the plane . A hexagon also has 6 edges as well as 6 internal and external angles .
6 is the second smallest composite number .[ 1] perfect number .[ 2] unitary perfect number , since it is the sum of its positive proper unitary divisors , without including itself. Only five such numbers are known to exist.[ 3] all-Harshad numbers .[ 4]
6 is the 2nd superior highly composite number ,[ 5] colossally abundant number ,[ 6] triangular number ,[ 7] highly composite number ,[ 8] pronic number ,[ 9] congruent number ,[ 10] harmonic divisor number ,[ 11] semiprime .[ 12] Granville number , or
S
{\displaystyle {\mathcal {S}}}
Golomb ruler of length 6 is a "perfect ruler".[ 13]
The six exponentials theorem guarantees that under certain conditions one of a set of six exponentials is transcendental .[ 14] abelian group is the symmetric group
S
3
{\displaystyle \mathrm {S_{3}} }
3! = 6 elements.[ 1] kissing number problem .[ 15]
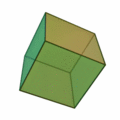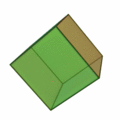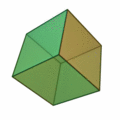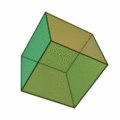
A regular cube , with six faces A cube has 6 faces . A tetrahedron has 6 edges . In four dimensions , there are a total of six convex regular polytopes .
In the classification of finite simple groups , twenty of twenty-six sporadic groups in the happy family are part of three families of groups which divide the order of the friendly giant , the largest sporadic group: five first generation Mathieu groups , seven second generation subquotients of the Leech lattice , and eight third generation subgroups of the friendly giant. The remaining six sporadic groups do not divide the order of the friendly giant, which are termed the pariahs Ly O'N Ru J 4 J 3 J 1 [ 16]
List of basic calculations
Division
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6 ÷ x
6
3
2
1.5
1.2
1
0.857142
0.75
0.6
0.6
0.54
0.5
0.461538
0.428571
0.4
x ÷ 60.16
0.3
0.5
0.6
0.83
1
1.16
1.3
1.5
1.6
1.83
2
2.16
2.3
2.5
Exponentiation
1
2
3
4
5
6
7
8
9
10
11
12
13
6x
6
36
216
1296
7776
46656
279936
1679616
10077696
60466176
362797056
2176782336
13060694016
x 6 1
64
729
4096
15625
46656
117649
262144
531441
1000000
1771561
2985984
4826809
Greek and Latin word parts
Hexa Hexa Greek for "six".[ 1]
The prefix sex-
Sex- Latin prefix meaning "six".[ 1]
Senary is the ordinal adjective meaning "sixth"[ 20] People with sexdactyly have six fingers on each hand
The measuring instrument called a sextant got its name because its shape forms one-sixth of a whole circle
A group of six musicians is called a sextet
Six babies delivered in one birth are sextuplets
Sexy prime pairs – Prime pairs differing by six are sexy , because sex is the Latin word for six.[ 21] [ 22] The SI prefix for 10006 is exa- (E), and for its reciprocal atto- (a).
Evolution of the Hindu-Arabic digit
The first appearance of 6 is in the Edicts of Ashoka c. 250 BCE . These are Brahmi numerals , ancestors of Hindu-Arabic numerals. The first known digit "6" in the number "256" in Ashoka's Minor Rock Edict No.1 in Sasaram , c. 250 BCE The evolution of our modern digit 6 appears rather simple when compared with the other digits. The modern 6 can be traced back to the Brahmi numerals of India , which are first known from the Edicts of Ashoka c. 250 BCE .[ 23] [ 24] [ 25] [ 26] [ 27]
On the seven-segment displays of calculators and watches, 6 is usually written with six segments. Some historical calculator models use just five segments for the 6, by omitting the top horizontal bar. This glyph variant has not caught on; for calculators that can display results in hexadecimal, a 6 that looks like a "b" is not practical.
Just as in most modern typefaces , in typefaces with text figures the character for the digit 6 usually has an ascender , as, for example, in [ 28]
This digit resembles an inverted 9 . To disambiguate the two on objects and documents that can be inverted, the 6 has often been underlined, both in handwriting and on printed labels.
The cells of a beehive are six-sided.
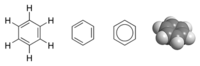
Chemistry
A molecule of benzene has a ring of six carbon and six hydrogen atoms .
Anthropology
See also
References
^ a b c d e f Weisstein, Eric W. "6" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Higgins, Peter (2008). Number Story: From Counting to Cryptography 11 . ISBN 978-1-84800-000-1 ^ Sloane, N. J. A. (ed.). "Sequence A002827 (Unitary perfect numbers)" . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. Retrieved 2016-06-01 .^ Weisstein, Eric W. "Harshad Number" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ "A002201 - OEIS" . oeis.org . Retrieved 2024-11-28 .^ "A004490 - OEIS" . oeis.org . Retrieved 2024-11-28 .^ "A000217 - OEIS" . oeis.org . Retrieved 2024-11-28 .^ "A002182 - OEIS" . oeis.org . Retrieved 2024-11-28 .^ "Sloane's A002378: Pronic numbers" . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. Retrieved 2020-11-30 .^ Sloane, N. J. A. (ed.). "Sequence A003273 (Congruent numbers)" . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. Retrieved 2016-06-01 .^ "A001599 - OEIS" . oeis.org . Retrieved 2024-11-28 .^ Sloane, N. J. A. (ed.). "Sequence A001358 (Semiprimes (or biprimes): products of two primes.)" . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. Retrieved 2023-08-03 .^ Bryan Bunch, The Kingdom of Infinite Number . New York: W. H. Freeman & Company (2000): 72
^ Weisstein, Eric W. "Six Exponentials Theorem" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Weisstein, Eric W. "Kissing Number" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Griess, Jr., Robert L. (1982). "The Friendly Giant" (PDF) . Inventiones Mathematicae 69 : 91– 96. Bibcode :1982InMat..69....1G . doi :10.1007/BF01389186 . hdl :2027.42/46608 . MR 0671653 . S2CID 123597150 . Zbl 0498.20013 . ^ Weisstein, Eric W. "Hexadecimal" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Weisstein, Eric W. "Hexagon" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Weisstein, Eric W. "Hexahedron" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Weisstein, Eric W. "Base" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Chris K. Caldwell; G. L. Honaker Jr. (2009). Prime Curios!: The Dictionary of Prime Number Trivia ISBN 978-1-4486-5170-2 ^ Weisstein, Eric W. "Sexy Primes" . mathworld.wolfram.com . Retrieved 2020-08-03 . ^ Hollingdale, Stuart (2014). Makers of Mathematics 95– 96. ISBN 978-0-486-17450-1 ^ Publishing, Britannica Educational (2009). The Britannica Guide to Theories and Ideas That Changed the Modern World ISBN 978-1-61530-063-1 ^ Katz, Victor J.; Parshall, Karen Hunger (2014). Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century ISBN 978-1-4008-5052-5 ^ Pillis, John de (2002). 777 Mathematical Conversation Starters ISBN 978-0-88385-540-9 ^ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 395, Fig. 24.66
^ Negru, John (1988). Computer Typesetting ISBN 978-0-442-26696-7 slight ascenders that rise above the cap height ( in 4 and 6 ) ^ Webb, Stephen; Webb, Professor of Australian Studies Stephen (2004-05-25). Out of this World: Colliding Universes, Branes, Strings, and Other Wild Ideas of Modern Physics ISBN 978-0-387-02930-6 snowflake, with its familiar sixfold rotational symmetry ^ Rimes, Wendy (2016-04-01). "The Reason Why The Dead Are Buried Six Feet Below The Ground" . Elite Readers . Retrieved 2020-08-06 . ^ "Chinese Numbers 1 to 10 | maayot". maayot • Bite-size daily Chinese stories . 2021-11-22. Retrieved 2025-01-17.
^ Smith, Michael (2011-10-31). Six: The Real James Bonds 1909-1939 ISBN 978-1-84954-264-7
External links
Look up
six in Wiktionary, the free dictionary.
100,000 1,000,000 10,000,000 100,000,000 1,000,000,000