|
Teorema de Menelau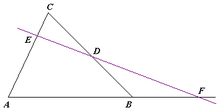 E, D i F estan alineats, per tant, s'ha de complir la relació que es mostra al text. Cal tenir en compte que, en aquest cas, la longitud BF pren valor negatiu. En geometria euclidiana, el teorema de Menelau, atribuït a Menelau d'Alexandria, estableix la condició suficient i necessària perquè tres punts diferents situats a cada un dels costats d'un triangle, o a les prolongacions d'aquests, estiguin alineats. Donat un triangle amb vèrtexs A, B i C, i donats els punts D, E i F que pertanyen a les rectes dels costats BC, AC i AB, respectivament, llavors el teorema de Menelau estableix que D, E i F estan alineats si i només si es compleix la següent relació:[1] on AF, per exemple, representa la longitud del segment lineal que va des del punt A fins al punt F. Cal tenir en compte que en la igualtat anterior es permet que la longitud dels segments prengui valors negatius. La longitud d'un segment prendrà valor negatiu en cas que aquest segment no se superposi més que per un punt amb el costat del triangle, és a dir, quan només comparteixin el vèrtex. En canvi, prendrà valor positiu sempre que el segment se superposi amb el costat del triangle per més d'un punt. El teorema de Menelau és molt similar al teorema de Ceva en el sentit que tenen equacions que difereixen només en el signe. A més, la representació gràfica d'un és la dual de l'altra. Ambdós poden demostrar-se a partir de l'altre.[2] HistòriaMenelau d'Alexandria va ser un matemàtic i astrònom grec del segle i. En el Llibre III de la seva obra titulada Esfèriques hi va demostrar la versió esfèrica del teorema, aplicable a la geometria de l'esfera celeste. La demostració utilitzava cinc proposicions, que donava per conegudes, i una d'elles era la versió plana del teorema (tractada en aquest article). El llibre es va perdre i la demostració es va difondre posteriorment a través de l'obra Almagest de Claudi Ptolemeu, que també incloïa la demostració de les proposicions.[3][4] Demostració En primer lloc, cal demostrar que el signe de la part esquerra de l'equació sempre serà negatiu. Anomenem f la recta que passa pels punts D, E i F, i veiem que f pot intersectar o bé cap o bé dos dels costats del triangle. En conseqüència, hi haurà un nombre senar de talls amb les prolongacions i, per tant, un nombre senar de segments amb longitud negativa. Per les propietats de la multiplicació, una quantitat senar de nombres negatius multiplicant-se amb qualsevol quantitat de nombres positius dona sempre com a resultat un nombre negatiu. En segon lloc, cal demostrar amb valors absoluts que quan els tres punts estan alineats, l'equació es compleix. Prenent la recta f que hem definit abans, considerem els segments BL, AM i CN perpendiculars a f tals que L, M i N pertanyen a f. Aleshores, tots tres segments són paral·lels. Aplicant el teorema de Tales:
I multiplicant aquestes equacions: En darrer lloc, cal demostrar que si l'equació es compleix, els tres punts estaran alineats. Suposem que l'equació es compleix. Considerem la recta definida pels punts D i E, anomenem-la s. Aquest recta talla el costat AB, o la seva prolongació, en un punt G. I com ja hem demostrat es compleix l'equació: Igualant-la amb l'equació original: Els punts F i G pertanyen a AB, o la seva prolongació, i s'hi situen amb una mateixa relació de distàncies respecte a A i a B, i per tant, coincideixen. En conseqüència, D, E i F estan alineats. Q.E.D.[5] Referències
|







