|
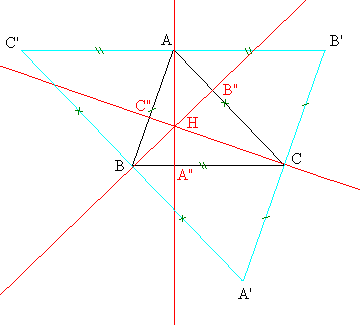
Altura (geometria) En geometria l'altura és la línia imaginària que es pot traçar des d'un vèrtex, o des del pla superior, d'una figura geomètrica fins a la base, i de manera perpendicular a aquesta. Per extensió, és també la longitud d'aquesta línia. L'altura, juntament amb la base, el radi, el nombre π i altres magnituds similars, es prenen sovint com a factors per a calcular les àrees i els volums de les figures a què pertanyen. Altura en tres dimensionsL'altura d'un objecte o figura geomètrica és una longitud o una distància, usualment vertical o en la direcció de la gravetat. Aquest terme també s'usa per designar la coordenada vertical de la part més elevada d'un objecte. En coordenades cartesianes (x, y, z), l'altura dels volums correspon a la coordenada Z que és la que se situa perpendicular a terra (vertical), normalment, ja que X i Y són assignats a valors horitzontals: amplada (o ample) i longitud (o llarg). Popularment, el substantiu «altura» pot ser reemplaçat per «alt» (adjectiu substantivat), que el DIEC accepta com desena accepció.[1] Altura en figures planesEn figures contingudes en el pla euclidià, l'altura és la distància perpendicular a un eix horitzontal fixat per convenció. En coordenades cartesianes (x, y), en el pla, l'altura es refereix a la distància perpendicular a l'eix X, o la longitud d'un segment paral·lel a l'eix Y. En un paral·lelepípede, l'altura és la menor distància entre els dos costats paral·lels. En un quadrilàter amb almenys dos costats paral·lels, l'altura és la menor distància entre els dos costats paral·lels. Altures d'un triangleEn un triangle l'altura respecte d'un costat, és la distància entre la recta que conté al costat i el vèrtex oposat. Equival a un segment perpendicular a aquest costat amb un extrem en el vèrtex oposat i l'altre en aquest costat, o en la seva prolongació. La intersecció de l'altura i el costat oposat es denomina «peu» de l'altura. A la figura, les altures respecte dels seus tres costats BC, CA i AB són AA ", BB" i CC ". La magnitud de l'altura serveix per calcular l'àrea d'un triangle i el seu valor: a = b · h/2, on a és l'àrea, b la base (la longitud del costat "inferior"), i h la seva altura corresponent. A la figura, poden ser BC · AA "/2, Ab-CC"/2 o AC · BB "/2. Aquesta fórmula es pot demostrar, geomètricament, traçant un rectangle amb una àrea doble de l'àrea del triangle, amb la mateixa base i la mateixa altura. 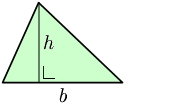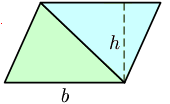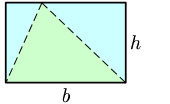 Característiques i propietats de les altures del triangle: En tot triangle:
Vegeu tambéNotes
|