|
Batlamyus
 Quadripartitum, 1622 Klaudyos Batlamyus (Grekçe: Κλαύδιος Πτολεμαίος Klaudios Ptolemaios), İskenderiyeli Yunan matematikçi, coğrafyacı, astronom ve müzik teorisyeniydi[2] ve üçü daha sonra Bizans, İslam ve Batı Avrupa bilimi için önemli olan yaklaşık bir düzine bilimsel tez yazmıştır. MS 100-170 yılları arasında yaşadığı tahmin edilmektedir.[3] Geç İskenderiye Dönemi'nde yaşamış (MS 2. yüzyılın ilk yarısı) ünlü bilim adamlarındandır. Hayatı hakkında hemen hemen hiçbir bilgi bulunmamaktadır. Müslüman astronomlar 78 yaşına kadar yaşadığını söylemektedir.[kaynak belirtilmeli] Yunan asıllı bir Mısırlı veya Mısır asıllı bir Yunan olduğu iddia edilmektedir.[kaynak belirtilmeli] KitaplarıBatlamyus, iki önemli yapıtın yazarıdır: Büyük Bileşim ve Coğrafya. Bu yapıtlar Avrupa'daki Orta Çağ'ın bitişinde önemli yere sahiptir. Kitapların Latinceye çevrilişi ancak 12. yüzyılda yapılmıştır.
Batlamyus astronomi, matematik, coğrafya ve optik alanlarına katkılar yapmıştır; ancak en çok astronomi çalışmalarıyla tanınır. Zamanına kadar ulaşan astronomi bilgisinin sentezini yapmış ve bunları Mathematike Syntaxis (Matematik Sentezi) adlı yapıtında toplamıştır. Bu eser daha sonra Megale Syntaxis (Büyük Derleme) olarak anılmış ve Arapçaya çevrilirken başına harf-i tarif takısı olan el- getirildiği için, ismi el-Mecistî biçimine dönüşmüştür; daha sonra Arapçadan Latinceye çevrilirken Almagest olarak adlandırıldığından, bugün Batı dünyasında bu eser Almagest adıyla tanınmaktadır. Almagest, on üç kitaptan oluşur;
Batlamyus bu eserde, ana çizgileriyle göksel olguları anlamlandırmak üzere kurmuş olduğu geometrik kuramı tanıtmaktadır; Aristoteles fiziğini temel alan bu kuramda, evren küreseldir ve Yer bu evrenin merkezinde hareketsiz olarak durmaktadır. Şayet günlük veya yıllık görünümler Yer'in hareketleri sonucunda meydana gelseydi, her şey uzaya saçılır ve Yer parçalanırdı. Ay, Merkür, Venüs, Güneş, Mars, Jüpiter, Satürn ve sabit yıldızlar Yer'in çevresinde, muntazam hızlarla, dairesel hareketler yaparlar. Sabit yıldızlar küresi evrenin sonudur. Ancak, Yer'in merkezde olduğu ve gök cisimlerinin de onun çevresinde düzenli olarak dolandıkları kabul edildiğinde, bazı gözlemleri, örneğin Ay ve Güneş'in Yer'e yaklaşıp uzaklaşmalarını, bazen hızlı ve en kapsamlı bilgiler vermiştir; çünkü küresel astronominin sınırları içinde kalan klasik astronomiye ait hesaplamalar, küresel geometriye dayanmaktadır. Batlamyus'tan yaklaşık üç asır önce yaşamış olan Hipparkhos (MÖ 150) açıların kirişlerle ölçülebileceğini bildirmiş ve bir kirişler cetveli hazırlamıştı; ancak konuya ilişkin yapıtı kaybolduğundan, bu cetveli nasıl düzenlediği bilinmemektedir. Bazı yayların kirişlerinin bulunması çok kolaydı ve bu kirişlere ana kirişler adı verilmişti; ama bunların dışındaki yayların kirişlerinin bulunması uzun işlemleri gerektiriyordu. Bu nedenle Batlamyus kirişler cetvelini hazırlarken bir dairenin içine çizilmiş dörtgenlere ilişkin Batlamyus Teoremi'ni (AB. CD + AD. BC = AC. BD) kullanmak suretiyle, açılar toplamı ve farkının kirişlerini (kiriş (A-B), kiriş (A+B), kiriş A/2, kiriş 2A gibi) bulma yoluna gitmişti. Coğrafya araştırmalarıBatlamyus, coğrafya araştırmalarına da öncülük etmiş ve Coğrafya adlı yapıtıyla matematiksel coğrafya alanını kurmuştur. Bu kitap Kristof Kolomb'a kadar bütün coğrafyacılar tarafından başvuru kitabı olarak kullanılmıştır.[5][sayfa belirt] Almagest'ten sonra yazılan Coğrafya, sekiz kitaba bölünmüştür ve matematiksel coğrafya ile haritaların çizilebilmesi için gerekli bilgilere tahsis edilmiştir; Almagest gibi Coğrafya da derleme bir eserdir; Batlamyus bu kitabı hazırlarken Eratosthenes, Hipparkhos, Strabon ve özellikle de Surlu Marinos'tan büyük ölçüde yararlanmıştır. 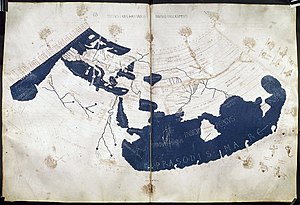 Batlamyus'un dünya haritasının 15. yüzyıl çizimi. Coğrafya'nın Birinci Kitabı, Dünya'nın -ya da doğrusunu söylemek gerekirse Yunanlar tarafından bilinen Dünya'nın- büyüklüğü ve kartografik izdüşüm yöntemleri hakkında ayrıntılı bilgiler verir.[5][sayfa belirt] İkinci Kitap'la Yedinci Kitap arasında, tanınmış memleketlerdeki önemli yerlerin, yani önemli kentlerin, dağların ve nehirlerin enlem ve boylamları verilerek Dünya'nın düzenli bir tasviri yapılır. Enlem ve boylamlardan, yani bir başlangıç dairesine olan uzaklıklardan söz eden ilk bilgin olan Batlamyus'un enlem ve boylam tablolarıyla betimlemeye çalıştığı Dünya, kabaca 20° güneyden, 65° kuzeye; batıdaki Kanarya Adaları'ndan, bunların yaklaşık olarak 180° doğusundaki bölgelere kadar uzanmaktadır. Bunun dışında kalan bölgeler ise Yunanlar ve dolayısıyla Batlamyus tarafından tanınmamaktadır. Batlamyus'un tahminlerinin başarısının şaşırtıcı bir başka nedeni daha vardı. Haritalı Coğrafya'nın hayatta kalan en eski el yazmaları, 12. yüzyılın sonlarında Bizans'tan gelmektedir.[5][sayfa belirt] Batlamyus'un kendi haritalarını çizdiğine dair somut bir kanıt yoktur. Bunun yerine, coğrafi verileri daha sonraki harita yapımcılarının uyarlamasına izin veren bir dizi sayı ve diyagram kullanarak dijital biçimde iletti. Belki de bu nedenle Batlamyus'u ilk dijital coğrafyacı olarak kabul etmeliyiz.[6] Söz konusu tablolar, haritaların çizilmesini olanaklı kılmaktadır ve belki? de bu haritalar eserin eski nüshalarında mevcuttur. Astronomi bilgilerini kapsayan Sekizinci Kitap'ta bunlara atıflar yapılmıştır. Ancak Batlamyus'un coğrafya anlayışı yeterince geniş değildir. İklim, doğal ürünler ve fiziki coğrafyaya giren konularla hiç ilgilenmemiştir. Başlangıç meridyenini sağlam bir şekilde belirleyemediği için, vermiş olduğu koordinatlar hatalıdır. Ayrıca, Yer'in büyüklüğü hakkındaki tahmini de doğru değildir. Ancak Kristof Kolomb bu yanlış tahminden cesaret alarak Batı'ya doğru gitmiş ve Kuzey Amerika'ya ulaşmıştır.[5][sayfa belirt] Optik araştırmaları Bir Orta Çağ sanatkârının Batlamyus icrası Aynı zamanda döneminin önde gelen optik araştırmacılarından olan Batlamyus, daha önceki optikçilerin çoğu gibi, görmenin gözden çıkan görsel ışınlar yoluyla oluştuğu görüşünü benimsemiştir. Ancak, görsel yayılımın fiziksel yorumunu da vermiş ve bu yayılımın, kesikli ve aralıklı koni biçiminde değil de, kesiksiz ve sürekliliği olan piramit biçiminde olduğunu belirtmiştir. Şayet böyle olmasaydı, yani ışınlar gözden sürekli olarak çıkmasaydı, nesneler bütün olarak görülemezlerdi. Buna rağmen, Batlamyus'un görsel piramit fikri, optikçiler arasında rağbet görmemiş ve görme söz konusu olduğunda daha çok koni biçimi göz önüne alınmıştır. Daha sonra da İslam dünyasında bilginlerin görsel koni fikrine dayandıkları ve görme geometrisini bunun üzerine kurdukları görülmektedir. Batlamyus, katoptrik (yansıma) konusuyla da ilgilenmiş ve ayrıntılı deneyler sonucunda üç prensip ileri sürmüştür:
Bu üç prensipten ilk ikisini kuramsal, üçüncüsünü ise deneysel olarak kanıtlayan Batlamyus, ayna yüzeyine gelen ışının eşit açıyla yansıdığını gösterebilmek için, derecelenmiş ve tabanına ayna yerleştirilmiş olan bakır bir levha kullanmıştır. Bir ışın hüzmesini levhaya teğet biçimde ayna yüzeyine gönderip, gelme ve yansıma açılarının büyüklüklerini belirlemiş ve bunların eşit olduğunu görmüştür. Batlamyus bu deneyini küresel ve parabolik bütün aynalar için tekrarlayarak, sonucun doğruluğunu kanıtlamıştır. Batlamyus, dioptrik (kırılma) konusuyla da ilgilenmiş ve ışığın bir ortamdan diğerine geçerken yoğunluk farkından dolayı yön değiştirmesinin nedenini araştırmıştır. Bu araştırmanın sonucunda, az yoğun ortamdan çok yoğun ortama geçen ışının, normale yaklaşarak ve çok yoğun ortamdan az yoğun ortama geçen ışının ise normalden uzaklaşarak kırıldığını ve kırılma miktarının yoğunluk farkına bağlı olduğunu ileri sürmüştür. Konuyu ele alırken benimsediği bazı prensiplerde bunu açıkça görmek olanaklıdır:
Batlamyus ortam farklılıklarından dolayı ışığın uğradığı değişimleri, aynı zamanda kırılma kanununu da içerecek şekilde deneysel olarak göstermeye çalışmış ve çeşitli ortamlardaki (havadan cama, havadan suya ve sudan cama) kırılma derecelerini gösteren cetveller hazırlamıştır. Ancak verdiği değerler küçük açılar dışında tutarlı olmadığı için kırılma kanununu elde edememiştir. Astrolojik çalışmalarıBatlamyus, daha önce Babil ve Yunan astronomları ve astrologları tarafından derlenmiş bilgi birikiminden yararlanarak astrolojiyi de sistematize etmiştir. Dört bölümden oluştuğu için Tetrabiblos (Dört Kitap) olarak adlandırdığı yapıtında, gezegenlerin nitelik ve etkileri, burçların özellikleri, uğurlu ve uğursuz günlerin belirlenmesi gibi astroloji kapsamındaki konular hakkında ayrıntılı bilgiler vermiştir. Orta Çağ ve Yeni Çağ astrolojisi bu kitabın sunmuş olduğu birikime dayanacaktır. Astroloji bir bilim değildir, ama astronomi ile birlikte doğmuş ve yaklaşık olarak 18. yüzyıl'a kadar bu bilimin gelişimini, kısmen olumlu kısmen de olumsuz yönde etkilemiştir; bu nedenle astronomi tarihi araştırmalarında astrolojiye ilişkin gelişmelerden de bahsetmek gerekir. Ayrıca bakınızKaynakça
|
||||||||||||||||||||||
