三角形

三角形
三角形
辺・頂点	3
シュレーフリ記号	{3} (等辺の場合)
面積	さまざまな方法： #三角形の面積を参照
内角 (度)	60°（等辺の場合）

初等幾何学における三角形（さんかくけい、さんかっけい、拉: triangulum, 独: Dreieck, 英, 仏: triangle,（古風）trigon）は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。その3点を三角形の頂点、3つの線分を三角形の辺という。

3点 A, B, C を頂点とする三角形は記号 △ を用いて △ABC と表記する。記号△はピエール・エリゴン（フランス語版）などが16世紀に使うようになった^[1]。

三角形の 2辺がなす角をその三角形の内角という。

図1においては、∠ABC が内角の 1つとなる。三角形は 3つの内角をもち、その和は平面上では2直角（180度）となる（本稿はユークリッド幾何学における三角形を論じる）。

また、∠ACD のように、1つの辺と、他の辺の延長が作る角を三角形の外角という。三角形の 1つの頂点（内角）に対して、内角をはさむ2辺以外の辺をその頂点（内角）の対辺という。また、三角形の 1つの辺に対して、辺の両端以外の頂点（内角）をその辺の対頂点（対角）という。

一般に、三角形の頂点やその頂点の内角を表すには、大文字のアルファベットを用いる。特に、内角（内角の大きさ）を表すときには、頂点の前に記号 ∠ をつけるか、頂点の文字を斜体にして表すのが慣例である。たとえば、図2 の頂点 B を持つ内角（内角の大きさ）を ∠B、または B と表す。

辺（辺の長さ）を表すには、対頂点（向かい合う頂点）の文字に対応する小文字のアルファベットで表すことが行われる。たとえば、図2 の角 B の対辺 CA は、b と表す。この記法は、18世紀のオイラーの頃から使われるようになった^[2]。

三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a，b，c とするとき、次の三つの不等式が成り立つ。

• a < b + c
• b < c + a
• c < a + b

この関係は三角不等式として一般化される。 逆に、この不等式が三つとも成り立てば、a，b，c を3辺の長さとする三角形を作ることができる。

• a < b ⇔ A < B
• b < c ⇔ B < C
• c < a ⇔ C < A

特に、三角形の最長辺（最短辺）と最大内角（最小内角）は向かい合う関係にある。

三角形の 3つの辺のうちの一つを底辺としたとき、その対頂点から底辺またはその延長に下ろした垂線が、三角形によって切り取られる線分（線分の長さ）を、三角形の高さという。底辺をどの辺と見るかによって、三角形には 3つの高さがある。

三角形の高さは、底辺と対頂点の距離に等しい。

底辺の中点と、対頂点を結ぶ線分を、三角形の中線という。底辺をどの辺と見るかによって、1つの三角形には 3本の中線がある。

三角形の中線は、三角形の面積を二等分する。

底辺を除く 2辺それぞれの中点を結ぶ線分を、三角形の中点連結という。底辺をどの辺と見るかによって、1つの三角形には 3つの中点連結がある。

三角形の中点連結は、底辺と平行で、長さは底辺の半分に等しい（中点連結定理）。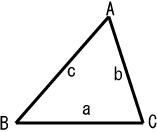

三角形は、その辺や角の大きさにより、いくつかの方法で分類することができる。

• 大きさが 0度より大きく 90度より小さい角を鋭角という。
• 大きさが 90度である角を直角という。
• 大きさが直角 90度より大きく、平角 180度より小さい角を鈍角という。

三角形の内角の和は 180度なので、三角形の内角で 90度以上のものは高々1個である。三角形の内角は、すべて鋭角であるか、直角1個と鋭角2個であるか、鈍角1個と鋭角2個、のいずれかである。

三角形を内角の大きさで分類するとき、内角が全て鋭角である三角形を鋭角三角形（図2）、1つの内角が直角である三角形を直角三角形（図4）、1つの内角が鈍角である三角形を鈍角三角形（図3）という。

また、三角形を辺の長さで分類するとき、3つの辺の長さがすべて異なる三角形を不等辺三角形（図2）という。

2つの辺の長さが等しい三角形を二等辺三角形（図5）という。

二等辺三角形のうち、直角三角形の直角をはさむ 2つの辺が等しいものを直角二等辺三角形（図6）という。

二等辺三角形のうち、3つの辺の長さがすべて等しい三角形を正三角形（図7）という。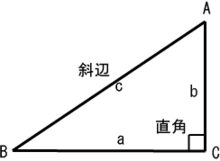

1つの内角が直角である三角形を直角三角形と呼ぶ。直角三角形の頂点のうち、内角が直角である頂点を直角頂と呼ぶ（図4）。

直角三角形の直角以外の内角 2つは 90度未満となり、これらを直角三角形の鋭角と呼ぶ。それらの和は直角に等しい。

直角三角形の直角の対辺を斜辺という。斜辺は、直角三角形の 3つの辺の中で最も長い辺である。斜辺でない 2辺を、直角をはさむ 2辺と呼ぶ。

直角をはさむ 2辺 a，b と、斜辺 c の間には、次の関係が成り立つ（ピタゴラスの定理）。

a² + b² = c²

逆に、△ABC の 3辺 a，b，c が上の等式を満たすならば、△ABC は辺 c を斜辺とする直角三角形となる（ピタゴラスの定理の逆）。

二等辺三角形において、長さの等しい 2つの辺を等辺といい、残りの 1つの辺を二等辺三角形の底辺と呼ぶ。2つの等辺のなす角を頂角といい、残りの 2つの内角を底角という。頂角の対辺が底辺であり、底辺の両端の角が底角である。また、二等辺三角形で頂点と言った場合、特に底辺の対頂点を指す。

△ABC が b = c の二等辺三角形であれば、底角 ∠B = ∠C であり（二等辺三角形の底角の性質）、逆に、△ABC の 2角が ∠B = ∠C であれば、b = c の二等辺三角形となる（二等辺三角形の成立条件）。

二等辺三角形は線対称な図形であり、頂角の二等分線、底辺の垂直二等分線、頂点から底辺に引いた中線はすべて対称軸上に乗る。

二等辺三角形のうち、頂角が直角であるものを直角二等辺三角形という。直角二等辺三角形においては、直角をはさむ 2辺を等辺、底辺を斜辺と呼ぶこともできる。2つの鋭角ないし底角の大きさは、それぞれ 45度となる（図6）。

二等辺三角形のうち、等辺と底辺の長さが等しいものを正三角形という。（図7）

正三角形の内角は全て等しく 60度となる。逆に、ある内角が 60度である二等辺三角形は正三角形である。

正三角形は正多角形の一種である。正多角形とは、全ての辺が等しく、全ての内角が等しい多角形と定義されるが、正三角形に限って3辺が等しいことのみで定義される。

正三角形には、対称軸が 3本ある。正三角形の重心、外心、内心、垂心、フェルマー点は、全て一致する。

平面図形である多角形には内部と外部があり、面積を考えることができる。中でも基本的である三角形の面積の求め方は、基本的なものだけでもいくつかが知られている。どの式で求めるかは、分かっている量（辺の長さや内角など）に応じて使い分ければよい。

1つの辺、またはその延長線と直角に交わる直線をその辺に立てた垂線といい、垂線と、その辺またはその延長の交点を垂線の足または垂足という。1つの辺に立てた垂線が、それに対する頂点を通るとき、垂線の足とその頂点を結んだ線分をその三角形の高さという。高さは 3つの辺それぞれに対して定義できる。頂点 A の対辺 a に対する高さを h_a とするとき、面積 S は

${\displaystyle S={\frac {1}{2}}ah_{a}}$ …①

で求められる。

3辺の長さを a, b, c とするとき、面積 S は

${\displaystyle S={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}$ …②

となるが、少し複雑なので、

${\displaystyle s={\frac {1}{2}}(a+b+c)}$（半周長）

とおくと、

${\displaystyle S={\sqrt {s(s-a)(s-b)(s-c)}}}$ …③

で求められる。これをヘロンの公式と呼ぶ。

しかし、数値計算する上で、上記でない形式の方が計算しやすい場合もある。a, b, c のうち少なくとも1つは無理数だが a², b², c² は整数の場合は、a² = A, b² = B, c² = C とおくと、

${\displaystyle S={\frac {1}{4}}{\sqrt {2(BC+CA+AB)-(A^{2}+B^{2}+C^{2})}}}$ …③'

が有用である。

1つの内角を C、それをはさむ2辺の長さを a, b とするとき、面積 S は

${\displaystyle S={\frac {1}{2}}ab\sin C}$ …④

で求められる。

この等式は、高さおよびsinの定義により、①から導くことができる。（①の ${\displaystyle h_{a}}$ は④の ${\displaystyle b\sin C}$ に等しいため）

1辺の長さを a、その両端の内角を B, C とするとき、面積 S は

${\displaystyle S={\frac {a^{2}\sin B\sin C}{2\sin(B+C)}}}$ …⑤

または

${\displaystyle S={\frac {a^{2}}{2(\cot B+\cot C)}}}$ …⑥

で求められる。

内接円の半径を r、3辺 a, b, c に接する傍接円の半径をそれぞれ r_a, r_b, r_c とするとき、面積 S は

${\displaystyle S={\sqrt {rr_{a}r_{b}r_{c}{\vphantom {A}}}}}$ …⑦

で求められる。

2次元直交座標平面で、原点を含む 3点 A(x_A, y_A), B(x_B, y_B), C(0, 0) を頂点とする三角形の場合、面積 S は

${\displaystyle S={\frac {1}{2}}|x_{\text{A}}y_{\text{B}}-x_{\text{B}}y_{\text{A}}|}$ …⑧

で求められる。

一般の 3点 A(x_A, y_A), B(x_B, y_B), C(x_C, y_C) を頂点とする三角形の場合、面積 S は

${\displaystyle S={\frac {1}{2}}|(x_{\text{A}}-x_{\text{C}})(y_{\text{B}}-y_{\text{C}})-(x_{\text{B}}-x_{\text{C}})(y_{\text{A}}-y_{\text{C}})|}$ …⑨

で求められる。

2次元極座標平面で、原点を含む 3点 A(r_A, θ_A), B(r_B, θ_B), C(0, 0) を頂点とする三角形の場合、面積 S は

${\displaystyle S={\frac {1}{2}}r_{\text{A}}r_{\text{B}}\sin |\theta _{\text{A}}-\theta _{\text{B}}|}$ …⑩

で求められる。

三角形は内心、外心、垂心、重心、傍心をもつ。これらを併せて五心という。

外心を O、重心を G、垂心を H とおくと、3点 O, G, H は一直線上にあり（この直線をオイラー線と呼ぶ）、また OG : GH = 1 : 2 である。

三角形の内角の二等分線 3本は 1点で交わる。これらの交点を三角形の内心という。三角形には、その内部に内心が 1つだけある。内心は各辺との距離が等しく、その距離を半径として、内心を中心とする円が描ける。この円を三角形の内接円といい、全ての辺に接する。三角形の内接円は、接点を除き三角形の内部にある。

三角形の辺の垂直二等分線 3本は 1点で交わる。これらの交点を外心という。外心は各頂点との距離が等しく、その距離を半径として、外心を中心とする円を描くことができる。この円を三角形の外接円といい、全ての頂点を通る。

三角形の外接円は、頂点を除き三角形の外部にあるが、外心は三角形の内部にあるとは限らない。鈍角三角形の場合は三角形の外部にあり、直角三角形の場合は斜辺の中点が外心となる。

三角形の頂点から対辺に下ろした垂線を高さといい、どの辺を底辺とするかによって三角形には高さが 3本ある。3本の高さは 1点で交わり、これらの交点を垂心という。三角形は 1つの垂心を持つが、垂心が三角形の内部にあるとは限らない。鈍角三角形の場合は三角形の外部にあり、直角三角形の場合は直角頂が垂心となる。

三角形の底辺の中点と対頂点を結ぶ線分を中線といい、どの辺を底辺とするかによって三角形には中線が 3本ある。3本の中線は 1点で交わり、これらの交点を重心という。三角形はその内部に、1つの重心をもつ。重心は中線を 2 : 1 に内分する。

三角形の 1つの内角と他の 2つの外角の二等分線は 1点で交わる。これらの交点を傍心（ぼうしん）という。三角形に傍心は 3つある。傍心は 1辺、他の2辺の延長線との距離が等しく、傍心を中心として半径がその距離である円を傍接円という。

三角形の 3つの辺またはその延長線上と距離が等しい点は、内心と傍心の併せて 4点ある。

三角形の五心（重心、内心、傍心、外心、垂心）の位置ベクトル ${\displaystyle {\boldsymbol {p}}}$ は、頂点の位置ベクトル ${\displaystyle {\boldsymbol {a}},{\boldsymbol {b}},{\boldsymbol {c}}}$ を用いて、一般式

${\displaystyle {\boldsymbol {p}}={\frac {w_{\text{A}}{\boldsymbol {a}}+w_{\text{B}}{\boldsymbol {b}}+w_{\text{C}}{\boldsymbol {c}}}{w_{\text{A}}+w_{\text{B}}+w_{\text{C}}}}}$

で表される。ここで ${\displaystyle w_{\text{A}},w_{\text{B}},w_{\text{C}}}$ は重みであり、中心ごとに次の表の通りとなる。${\displaystyle S}$ はヘロンの公式でも得られる三角形の面積。

	${\displaystyle w_{\text{A}}}$	${\displaystyle w_{\text{B}}}$	${\displaystyle w_{\text{C}}}$	${\displaystyle w_{\text{A}}+w_{\text{B}}+w_{\text{C}}}$
重心	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 3}$
内心	${\displaystyle a}$	${\displaystyle b}$	${\displaystyle c}$	${\displaystyle a+b+c}$
傍心	${\displaystyle -a}$	${\displaystyle b}$	${\displaystyle c}$	${\displaystyle -a+b+c}$
	${\displaystyle a}$	${\displaystyle -b}$	${\displaystyle c}$	${\displaystyle a-b+c}$
	${\displaystyle a}$	${\displaystyle b}$	${\displaystyle -c}$	${\displaystyle a+b-c}$
外心	${\displaystyle a^{2}(b^{2}+c^{2}-a^{2})}$	${\displaystyle b^{2}(c^{2}+a^{2}-b^{2})}$	${\displaystyle c^{2}(a^{2}+b^{2}-c^{2})}$	${\displaystyle 16S^{2}}$
垂心	${\displaystyle a^{4}-(b^{2}-c^{2})^{2}}$	${\displaystyle b^{4}-(c^{2}-a^{2})^{2}}$	${\displaystyle c^{4}-(a^{2}-b^{2})^{2}}$	${\displaystyle 16S^{2}}$

${\displaystyle a\equiv {\overline {\text{BC}}}={\sqrt {({\vec {\text{BC}}},{\vec {\text{BC}}})}},}$

${\displaystyle b\equiv {\overline {\text{CA}}}={\sqrt {({\vec {\text{CA}}},{\vec {\text{CA}}})}},}$

${\displaystyle c\equiv {\overline {\text{AB}}}={\sqrt {({\vec {\text{AB}}},{\vec {\text{AB}}})}},}$

${\displaystyle {\begin{aligned}16S^{2}&=16s(s-a)(s-b)(s-c)\\&=2(b^{2}c^{2}+c^{2}a^{2}+a^{2}b^{2})-(a^{4}+b^{4}+c^{4})\end{aligned}}}$

ただし、

${\displaystyle s={\frac {a+b+c}{2}}}$.

2つの三角形を移動して重ね合わせることができるとき、この 2つの三角形は合同である。ここで移動とは、平行移動、回転移動、対称移動からいくつかを合成したものである。

ある 2つの三角形について、以下の条件のうち 1つでも満たしていれば、その 2つの三角形は合同となる。これを三角形の合同条件という。この条件は「三つの条件のうち、どれかが与えられれば三角形は決定される」、「相似の特別な場合である」（これは一般の多角形についても成り立つ）と解釈することもできる。

三辺相等 (SSS)：3組の辺がそれぞれ等しい

二辺夾角（二辺夾角相等／SAS）：2組の辺とその間の角がそれぞれ等しい

二角夾辺（二角夾辺相等／一辺両端角相等／ASA）：2組の角とそれらに挟まれる辺がそれぞれ等しい：（1組の辺と両端の角がそれぞれ等しい）

また、三角形の内角の和が一定（180度）であることを考えれば、"ASA" において与えられる2角は、辺を挟む 2角でなくともよいことが分かる。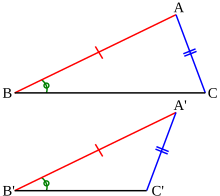

一方で、"SAS" においては、ただ単に 2辺と 1角が等しいだけは、合同とは限らない。例を図13 に示す。図13 では、△ABC と △A'B'C' について、AB = A'B', AC = A'C', ∠ABC = ∠A'B'C' であるが、合同でない。

特に、1角が直角である場合は、加えて次の合同条件も成立する。

斜辺一辺（斜辺一辺相等／RSS）：斜辺と他の 1辺がそれぞれ等しい

斜辺一鋭角（斜辺一鋭角相等／RAS）：斜辺と 1つの鋭角がそれぞれ等しい

ある2つの三角形について、以下の条件のうち1つでも満たしていれば、その2つの三角形は相似である。

三辺比相等：3組の辺の比がそれぞれ等しい

二辺比夾角（二辺比夾角相等）：2組の辺の比とその間の角がそれぞれ等しい

二角相等：2組の角がそれぞれ等しい

「三辺比相等」については、三角形の3辺の連比が等しいことを指す場合もある。

${\displaystyle a:b:c=a':b':c'\Leftrightarrow a:a'=b:b'=c:c'}$

よりこれらは同値である。ただし、日本の初等中等教育においては、3連比を導入していない段階では、この表現は避けられることがある。

特に、正三角形、直角二等辺三角形は、3つの内角の組が一定であるから、それぞれが互いに相似である。

• パスカルの三角形/タルタリアの三角形
• ライプニッツの調和三角形
• ハインリッヒの三角形
• 三角州
• 三角測量 - 三角点
• 三角貿易
• 三角町
• トライアングル（打楽器）
• 鉄のトライアングル
• 地域名
  • 黄金の三角地帯
  • バミューダ・トライアングル
  • ドラゴン・トライアングル
  • ポリネシアン・トライアングル
  • スンニー・トライアングル
• ナチ強制収容所のバッジ
  • ピンク・トライアングル
  • パープル・トライアングル
  • ブラック・トライアングル
• 夏の大三角
• 冬の大三角
• 春の大三角
• さんかく座
• みなみのさんかく座