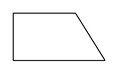
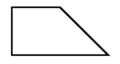
直角台形
直角台形
直角台形 (ちょっかくだいけい、英: Right angle trapezoid,Right-trapezoid) とは、四角形の一種である[1]。
概要
台形の一種で、2つの隣接する直角を持つ[2][3][4]。4つの内角で構成され、そのうちの2つは必ず90度である[5][6]。(右図)辺aに垂直な線dは、aに平行なすべての線にも垂直であるため、台形に少なくとも1つの直角がある場合、常に少なくとも2つの直角がある[7]。
直角台形が、3つの直角を持つことは不可能で、3つ目の角が90°の場合4つ目の角も90°になり、長方形になる[6]。
ギャラリー
脚注
- ^ “Right Trapezoid Formulas - xGeometry”. xgeometry.com. 2020年11月21日閲覧。
- ^ “Quadrilateral”. www.fz.dis.titech.ac.jp. 2020年11月21日閲覧。
- ^ “Right Trapezoid - Geometry Calculator”. rechneronline.de. 2020年11月21日閲覧。
- ^ “Right Trapezoid Formulas - xGeometry”. xgeometry.com. 2020年11月21日閲覧。
- ^ “Right-angled trapezoid”. www.gyplan.com.br. 2020年11月21日閲覧。
- ^ a b “Is it possible for a trapezoid to have a right angle?”. askinglot.com. 2020年11月21日閲覧。
- ^ “Right Trapezoid – Lexique de mathématique” (英語). 2020年11月21日閲覧。
関連項目
|
|---|
| 非古典的 (2辺以下) | |
|---|
| 辺の数: 3–10 |
|
|---|
| 辺の数: 11–20 | |
|---|
| 辺の数: 21–30 | |
|---|
| 辺の数: 31–40 | |
|---|
| 辺の数: 41–50 | |
|---|
辺の数: 51–70
(抜粋) | |
|---|
辺の数: 71–100
(抜粋) | |
|---|
辺の数: 101–
(抜粋) | |
|---|
| 無限 | |
|---|
星型多角形
(辺の数: 5–12) | |
|---|
| 多角形のクラス | |
|---|
|
|