|
סודוקו
סוּדוֹקוּ (ביפנית: 数独, מספר יחיד) הוא תשבץ מספרים שבו צריך למקם ספרות על לוח משובץ שגודלו (לרוב) 9×9, המורכב מ-9 מצולעים (בדרך כלל ריבועים, אך לא תמיד) בני 9 משבצות כל אחד. מטרת המשחק - למקם את 9 הסמלים (לרוב הספרות 1 עד 9) על גבי לוח המשחק כך שבכל טור, בכל שורה, ובכל מצולע יופיע כל סמל בדיוק פעם אחת. בלוח המשחק נתונים כמה סמלים, ויש להתייחס אליהם בעת מיקום הסמלים במהלך המשחק. התשבץ זכה לפופולריות ביפן בשנת 1986 ובבריטניה, בקנדה ובישראל בשנת 2005 בעקבות קידומו בעיתונות. יש חוקרים המייחסים לפתרון תשבצי סודוקו סגולות של שיפור או שימור כישורים שכליים[1]. היסטוריה במאה ה-18 חקר המתמטיקאי השווייצרי לאונרד אוילר ריבועים שבהם תוכן המשבצות שונה בכל שורה ובכל עמודה. הוא קרא לריבועים האלה "ריבועי קסם", אך כיוון שאוילר מילא את משבצות הריבועים באותיות לטיניות, מכנים אותם גם בשם "ריבועים לטיניים". משחק המבוסס על ריבועים לטיניים זה הופיע לראשונה בעיתון ניו יורקי בשם "Math Puzzles and Logic Problems" ("חידות מתמטיות ובעיות היגיון") בשנות ה-70 של המאה ה-20. גרסה ראשונה למשחק הסודוקו הופיעה ב־6 ביולי 1895 בעיתון הצרפתי La France[2]. המשחק במתכונתו הנוכחית הופיע לראשונה ב-1979 באחד המגזינים של דל מגזינס (Dell Magazines). גרסה זו הומצאה על ידי הווארד גארנס (Howard Garns), ארכיטקט אמריקאי בן 74 שפרש לגמלאות. גארנס לא רשם פטנט או תבע זכויות יוצרים, ובעקבות כך הסודוקו הפך להמצאה ברישיון חופשי ללא צורך בתמלוגים. משחק הסודוקו, שבו נדרש המילוי לקיים עוד תנאי נוסף, הופיע בראשונה ביפן בשנת 1984 ונקרא: "סואוז'י ווא דוקושין ני קאגירו" (数字は独身に限る) שמשמעו - "מוגבל למספר יחיד" (=היותו בלתי נשוי)". בהמשך קוצר השם ל"סודוקו", שמשמעו ביפנית (נוסף על היותו ראשי תיבות של הביטוי לעיל) "מספר יחיד" (数独). ניו זילנדי בשם ויין גולד, בעברו שופט בהונג קונג, פיתח תוכנית מחשב המייצרת תשבצים אלה, ובשנת 2004 החל לספקם לעיתון "הטיימס" הבריטי, אשר החל לפרסמם במדור יומי קבוע. כיום החידות מפורסמות ביפן ובבריטניה גם בעיתונים יומיים, וכן בעיתונים "New York Times" ו-"New York Post" בניו יורק. גם העיתונים האוסטרליים "האוסטרליאן" וה"סידני מורנינג הרלד" החלו בפרסום מדורים קבועים. בשנת 2005 גם עיתונים ישראליים החלו לפרסם סודוקו על בסיס קבוע. בישראל פורסם סודוקו בירחון התשבצים "ניקוי ראש ענק", עוד לפני שפשטה האופנה בעיתונים, תחת השם "תשע ברבוע". בירחון זה פורסמו גם שעשועוני קאקורו תחת השם "מספרים וסיכומים". הוראות המשחקבדרך כלל המשחק מתבצע על טבלה של 9×9 תאים (יש גם טבלות במידות אחרות), המסודרים בתשע תיבות של 3×3 תאים. בחלק מהתאים נמצאות ספרות, ויש להשלים ולמלא את התאים הריקים בספרות 1–9, כך שבכל טור, בכל שורה, ובכל תיבה, יופיעו כל הספרות. לחלופין, ניתן להגדיר שאסור שאותה ספרה תופיע פעמיים באותה שורה, טור או תיבה. הגדרות אלו שקולות זו לזו. שיטות פתרון שלב ראשוןשיטת הפתרון המומלצת היא חיפוש של מספרים החסרים באזורים (אזור=3X3 ריבועים) והשלמתם לפי המיקום האפשרי באזור. הדוגמה משמאל מציגה חיפוש היכן אפשר להציב את המספר 5 באזור הימני העליון. זוהי בעצם אלימינציה של המיקומים בהם המספר לא יוכל להשתבץ. שלב שנילאחר מעבר על כל המספרים, והשלמת המיקומים הוודאיים שלהם, נישאר עם מיקומים נוספים שבהם סימנו איזה מספרים יכולים להיות בהם. עכשיו אפשר לעבור על אזורים, שורות או עמודות שבהם נשארו מעט (2 או 3) ריבועים ריקים, ונבדוק איזה מספרים נשארו בהם ובאיזה מיקומים. כך נוכל להצליב שוב מספרים ומיקומים ולפתור עוד ריבועים. שלב שלישיככל שהתשבץ קשה יותר, יש יותר מיקומים שאין להם מספר ודאי שנזהה בשלבים שהצגנו. במקרה של תשבץ קשה נגיע לשלב שיש מיקומים עם מספר סימונים שאלימינציה לא פותרת וצריך להתחיל עם ניסוי וטעייה. יש לבחור צומת החלטה קריטי ולבחור בו אחת מהאפשרויות. צומת קריטי - מיקום בו יש מעט (עדיף 2) מספרים אפשריים, ובחירת מספר אחד תזהה בוודאות מספרים במיקומים אחרים. כך נמשיך עד שנפסול את האפשרות שבחרנו (תוביל לכפילות באזור, שורה או עמודה), או שנראה שהיא פותרת את התשבץ. האתגר הוא בחירת צומת ההחלטה הנכון שיוביל לפתרון. צומת לא טוב לא יקדם אותנו הרבה. פתרון ממוחשב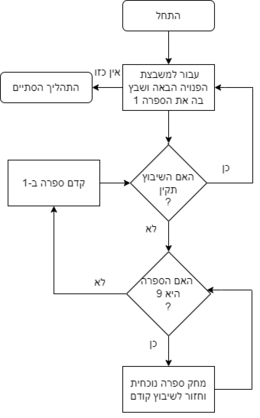 הדרך הפשוטה ביותר לפתור בעיות סודוקו באמצעות מחשב היא על ידי מעבר על כל האפשרויות, בשילוב של כוח גס וגישוש נסוג. מתחילים עם המשבצת הפנויה הראשונה, שמים בה את הספרה 1, ובודקים האם השיבוץ תקין, כלומר עומד בכללי הסודוקו. אם כן, ממשיכים למשבצת הפנויה הבאה ומבצעים בה אותו תהליך; אם לא - יש שתי אפשרויות: אם הספרה הנוכחית קטנה מ-9, מקדמים אותה ב-1 וחזקים לבדיקת התקינות; אחרת מוחקים את הספרה הנוכחית, חוזרים לצעד הקודם ובו אם הספרה קטנה מ-9, מקדמים אותה ב-1 וחזקים לבדיקת התקינות; אחרת מוחקים את הספרה, חוזרים לצעד הקודם, וכך הלאה. שיטה זו דורשת סיבוכיות זמן גבוהה למדי, ואינה מספקת הערכות לרמת הקושי של הפתרון. על כן רוב הפתרונות הממוחשבים מתבססים על הפעלת שיטות פתרון מהסוג שהודגם לעיל, ופונים לשימוש בגישוש נסוג רק כאמצעי אחרון (ראו אלגוריתמים לפתירת סודוקו (אנ')). בעיית פתירת הסודוקו ללוח בגודל משתנה ( שורות ועמודות ובלוקים בגודל ) ידועה כבעיה NP-שלמה. תחרויותבמרץ 2006 התקיימה בעיר לוקה, באיטליה אליפות העולם הראשונה לפתרון סודוקו. המשתתפים היו בני גילים שונים, מגיל 15 (המשתתף מגרמניה) ועד גיל 61 (המשתתף מאיטליה). באליפות השתתפו 85 איש מ-22 מדינות. כלכלנית ורואת חשבון צ'כית בת 31 בשם יאנה טיילובה (Jana Tylova) זכתה באליפות; היא הקדימה בדירוג את תומאס סניידר, בוגר אוניברסיטת הרווארד בן 26, שסיים במקום השני, ואת וויי-הא-הואן בן 30, מהנדס תוכנה בגוגל, קליפורניה, שסיים במקום השלישי. את הגביע העניק למנצחת השופט ויין גולד. אליפות העולם השנייה התקיימה במרץ 2007 בפראג, והפעם זכה תומאס סניידר (Thomas Snyder, שסיים במקום השני ב-2006). אליפות העולם השלישית התקיימה באפריל 2008 בגואה, ושוב זכה תומאס סניידר. נוסחים שונים      משחק של 9×9 הוא הנפוץ ביותר, אולם אפשריות גם חידות של 4 אזורים של 2×2, וכן חידות של 4 אזורים של 5×5. נוסח קשה במיוחד הוא של 16×16 משבצות עם 16 אזורים של 4×4. קיימות גם חידות פחות סימטריות של 6 אזורים של 2×3 וכן חידות של 8 אזורים של 2×4 ואף חידות של 12 אזורים של 3×4. לוחות סודוקו קטנים מהלוח הרגיל של 9*9, מיועדים בדרך כלל לילדים ונושאים את השם סובדוקו (Sub Doku). לוחות גדולים מהלוח הרגיל נושאים את השם סופרדוקו (Super Doku). כמו כן קיימת גרסאות מתקדמות יותר של הסודוקו:

סודוקו ומתמטיקהפתרון סודוקו תקף הוא גם ריבוע לטיני, תחום אשר נחקר רבות. קיימות הרבה פחות אפשרויות לסודוקו מאשר ריבועים לטיניים, משום שפתרון סודוקו דורש אילוץ נוסף, אזורי (הבלוקים). מספר האפשרויות לסודוקו של 9X9 הוא 6,670,903,752,021,072,936,960[5]. מספר זה שווה ל כאשר המספר האחרון הוא ראשוני. תוצאה זו חושבה בשיטות קומבינטוריות שנעזרו בחישוב "כוח גס" באמצעות מחשב. על אוסף הפתרונות פועלת מכפלה (לא ישרה) של החבורות (תמורה של הספרות), (שינוי סדר השורות או העמודות בכל בלוק, וערבוב הבלוקים) ו- (סימטריות של הריבוע)[6]. מספר מחלקות השקילות ביחס לפעולה הזו, הוא 5,472,730,538. זהו, אם כך, מספר הפתרונות השונים עקרונית זה מזה. המספר המקסימלי של נתונים שניתן לספק מבלי שהפתרון יקבע ביחידות הוא גודל הלוח עצמו פחות 4. למשל: אם חסרים שני מספרים בתאים שהם פינות של מלבנים מאונכים, אזי קיימות שתי דרכים לשבצם. המספר המינימלי של נתונים שיש לספק על מנת שהפתרון יקבע באופן יחידני עבור חידת סודוקו הוא 17, דבר זה הוכח ב-2012 על ידי חישוב מסיבי כחלק מהוכחה באמצעות מחשב. ידועות דוגמאות עם מספר נתונים זה. ראו גםלקריאה נוספת
קישורים חיצוניים
הערות שוליים
|








