fr Théorème de Thévenin

Le théorème de Thévenin aurait peut-être été démontré par le scientifique allemand Hermann von Helmholtz en 1853 ^{[réf. nécessaire]}, puis en 1883 par l'ingénieur en télégraphie français Léon Charles Thévenin. Ce théorème se déduit principalement des propriétés de linéarité^[1] et du principe de superposition qui en découle. Il s'utilise pour convertir une partie d'un réseau complexe en un dipôle plus simple.

Énoncé

Un réseau électrique linéaire vu de deux points est équivalent à un générateur de tension parfait dont la force électromotrice est égale à la différence de potentiels à vide entre ces deux points, en série avec une résistance égale à celle que l'on mesure entre les deux points lorsque les générateurs indépendants sont rendus passifs.

Démonstration du théorème de Thévenin

La démonstration de ce théorème repose sur le principe de superposition, ce qui permet d'étendre la généralité de son application à tout dispositif électronique qui fonctionne linéairement.

La démarche utilisée pour prouver ce théorème consiste tout d'abord à trouver un schéma équivalent pour un dipôle linéaire A de sorte que son comportement vis-à-vis d'un autre dipôle linéaire B reste identique lorsque ces deux dipôles sont reliés entre eux.

Avant de relier les dipôles A et B, les tensions à vide entre leurs bornes sont respectivement $u_{A}(t)=u_{A0}(t)\,$ et $u_{B}(t)\,=0$ car le dipôle B est supposé dans un premier temps, afin de simplifier la démonstration, ne pas contenir de sources électriques et avoir donc toutes ses grandeurs électriques en circuit-ouvert initialement nulles (figure a).

Les deux dipôles sont ensuite reliés à l'aide d'un court-circuit qui est remplacé de manière équivalente par deux sources de tension en série $u_{1}\,$ et $u_{2}\,$ qui ont une même amplitude égale à $u_{A0}(t)\,$ mais des orientations opposées (figure b). Dans ce nouveau montage, les courants et tensions se voient alors, par application du principe de superposition, comme le résultat de l'action cumulée de deux influences: celle de $u_{1}\,$ et des sources électriques situées dans A d'une part (figure c) et celle de $u_{2}\,$ d'autre part (figure d). La première de ces influences est cependant équivalente à la situation où, au préalable, les deux dipôles se trouvaient en circuit ouvert, elle ne modifie donc pas les grandeurs électriques de B. Ainsi, l'unique source de tension $u_{2}\,$ d'amplitude $u_{A0}(t)\,$ , la tension de Thévenin, mise en série avec le dipôle A dans lequel a été annulée l'influence de toutes les sources électriques indépendantes, la résistance de Thévenin, peut sembler être à l'origine des courants et tensions présents dans le dipôle B.

Lorsque le dipôle B contient également des sources électriques indépendantes, le principe de superposition permet encore de revenir à la situation de la démonstration précédente. Il suffit alors d'annuler les sources électriques indépendantes tour à tour dans chaque dipôle pour déterminer successivement les dipôles de Thévenin équivalents à A et à B.

Détermination du modèle de Thévenin

Soit un circuit composé de plusieurs sources et de plusieurs résistances possédant deux bornes A et B entre lesquelles est raccordée une charge :

La tension de Thévenin $U_{Th}\!$ est la tension calculée ou mesurée, entre les bornes A et B lorsque la charge est déconnectée (tension à vide).
La résistance de Thévenin $R_{Th}\!$ est la résistance calculée, ou mesurée, entre les bornes A et B lorsque la charge est déconnectée et que les sources sont éteintes : les sources de tension indépendantes sont remplacées par un court-circuit et les sources de courant indépendantes par un circuit ouvert.

Lorsque la tension de Thévenin est connue, il existe trois autres méthodes pratiques pour mesurer la résistance de Thévenin.

La première consiste à remplacer la charge par une résistance dont la valeur est connue et à prendre la tension aux bornes de cette résistance. $R_{Th}\!$ se résout facilement car elle devient alors la seule inconnue de l'équation découlant du théorème du diviseur de tension.
La deuxième méthode, proche de la première, est celle dite de la demi-tension : on utilise une résistance variable au lieu d'une résistance fixe et on fait varier la valeur de la résistance jusqu'à avoir ${\frac {U_{Th}}{2}}$ , les deux résistances sont alors égales.
La dernière méthode fait appel au courant de Norton. Si celui-ci est connu, on utilise la formule suivante: $R_{Th}=U_{Th}/I_{N}\!$ où $I_{N}\!$ est le courant calculé ou mesuré, entre les bornes A et B lorsqu'elles sont court-circuitées.

Le théorème de Thévenin s'applique aussi aux réseaux alimentés par des sources alternatives. L'ensemble des résultats est applicable en considérant la notion d'impédance en lieu et place de celle de résistance.

Exemple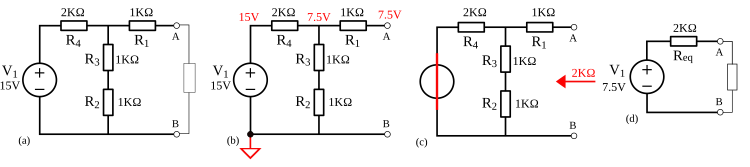

En (a) : Circuit original.
En (b) : Calcul de la tension aux bornes de AB, on utilise le diviseur de tension.

U_{\mathrm {AB} }={R_{2}+R_{3} \over (R_{2}+R_{3})+R_{4}}\cdot V_{\mathrm {1} }={1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega  \over (1\ \mathrm {k} \Omega +1\ \mathrm {k} \Omega )+2\ \mathrm {k} \Omega }\times 15\ \mathrm {V} ={1 \over 2}\times 15\ \mathrm {V} =7{,}5\ \mathrm {V}

(Notez que R₁ n'est pas prise en considération, car les calculs ci-dessus sont faits en circuit ouvert entre A et B, par suite, il n'y a pas de courant qui passe à travers R₁ et donc aucune chute de tension n'y apparait)

En (c) : Calcul de la résistance équivalente aux bornes AB en court-circuitant V₁ (A || B signifie une association de résistances parallèles).

R_{\mathrm {AB} }=R_{1}+\left(\left(R_{2}+R_{3}\right)\|R_{4}\right)=1\ \mathrm {k} \Omega +\left(\left(1\ \mathrm {k} \Omega +1\ \mathrm {k} \Omega \right)\|2\ \mathrm {k} \Omega \right)

=1\ \mathrm {k} \Omega +\left({1 \over (1\ \mathrm {k} \Omega +1\ \mathrm {k} \Omega )}+{1 \over (2\ \mathrm {k} \Omega )}\right)^{-1}=2\ \mathrm {k} \Omega

En (d) : Circuit équivalent de Thévenin. Celui-ci nous permet de trouver aisément le courant dans un dipôle quelconque relié entre les bornes A et B sans que l'on ait à résoudre le circuit au complet.

Conversion entre un circuit de Thévenin et de Norton

On passe directement d'un circuit de Thévenin à un circuit de Norton et inversement, à l'aide des formules suivantes :

De Thévenin à Norton ;

R_{N}=R_{Th},\quad I_{N}=U_{Th}/R_{Th}\!

De Norton à Thévenin ;

R_{Th}=R_{N},\quad U_{Th}=I_{N}R_{N}\!

Notes et références

↑ José-Philippe Pérez, « La main à la pâte, oui mais avec la Tête ! », Bulletin de l'union des physiciens, n°906, juillet/août/septembre 2008, page 988.

Léon C. Thévenin, « Extension de la loi d’Ohm aux circuits électromoteurs complexes », dans Annales Télégraphiques, tome 10, 1883, p. 222-224
Léon C. Thévenin, « Sur un nouveau théorème d’électricité dynamique », dans Compte rendu des Séances de l’Académie des Sciences, 1883, p. 159-161

Voir aussi

(fr) Le théorème de Norton et Thévenin (Electro-Robot)

Sur les autres projets Wikimedia :

Théorème de Thévenin, sur Wikimedia Commons
Théorème de Thévenin, sur Wikiversity

Articles connexes

Théorème de Norton
Électricité
Lois de Kirchhoff (loi des mailles et loi des nœuds)
Loi d'Ohm
Principe de superposition
Théorème de Millman
Théorème de réciprocité (électricité)
Théorème de Tellegen
Circuit ouvert

Liens externes

[PDF] (en) Introduction du théorème de Thévenin.
[PDF] (en) Historique du concept de circuit équivalent.
(en) Autres preuves du théorème:[1], [2], [3],[4].

[1] José-Philippe Pérez, « La main à la pâte, oui mais avec la Tête ! », Bulletin de l'union des physiciens, n°906, juillet/août/septembre 2008, page 988.

[1]

Agama	Bahasa	Biografi	Budaya	Ekonomi	Elektronika
Film	Filsafat	Geografi	Indonesia	Ilmu	Lingkungan
Masyarakat	Matematika	Militer	Mitologi	Musik	Olahraga
Pendidikan	Politik	Sastra	Sejarah	Seni	Teknologi

Théorème de Thévenin