Loi d'Ohm

Pour les articles homonymes, voir Ohm.

La loi d'Ohm est une loi physique empirique qui lie l'intensité du courant électrique traversant un dipôle électrique à la tension à ses bornes. Cette loi permet de déterminer la valeur d'une résistance^[1]. La loi d'Ohm a été ainsi nommée en référence au physicien allemand Georg Simon Ohm qui la publie en 1827, dans son œuvre Die galvanische Kette: mathematisch bearbeitet^[2].

On note :

• U la tension aux bornes de la résistance ;
• I l’intensité du courant qui circule à travers la résistance ;
• R la valeur de la résistance.

La loi d'Ohm établit que (en convention récepteur) :$${\displaystyle U=R\times I}$$

Un conducteur ohmique est un dipôle vérifiant la loi d'Ohm.

Dans la loi d'Ohm, la tension est exprimée en volts (V), la résistance en ohms (Ω) et l’intensité en ampères (A).

La loi d’Ohm indique que la tension aux bornes d’une résistance est proportionnelle à l’intensité du courant qui la traverse. Ce coefficient de proportionnalité est la valeur de la résistance.

La valeur de la résistance R est une constante et ne varie donc pas lorsque l'on modifie la tension ou l'intensité.

Selon son expression et les grandeurs connues, la loi d’Ohm permet d’obtenir différentes grandeurs :

• sous la forme U = R × I, elle permet de calculer la tension lorsque la résistance et l’intensité sont connues ;
• sous la forme I = U / R, elle permet de calculer l’intensité lorsque la tension et la résistance sont connues ;
• sous la forme R = U / I, elle permet de calculer la résistance lorsque la tension et l’intensité sont connues^[3].

Lorsqu'on trace la caractéristique d'un conducteur ohmique (c'est-à-dire le graphique de la tension en fonction de l'intensité), on obtient une droite passant par l'origine^[4]. La pente de cette droite est la valeur de la résistance.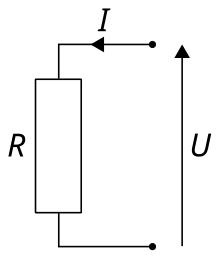

La différence de potentiel ou tension U (en volts) aux bornes d'un résistor de résistance R (en ohms) est proportionnelle à l'intensité du courant électrique I (en ampères) qui la traverse, ou la résistance R d'un dipôle est égale au quotient de sa tension U par l'intensité I du courant :

${\displaystyle U=R\cdot I}$

avec U et I orientées en sens opposés (dipôle en convention récepteur^{[N 1]}).

N.B. : si U et I sont orientées dans le même sens (dipôle en convention générateur), la loi devient alors :

${\displaystyle -\,U=R\cdot I}$.

On peut en déduire :

${\displaystyle I={\frac {U}{R}}}$^{[N 2]} ou ${\displaystyle R={\frac {U}{I}}}$^{[N 3]}.

Cette loi porte le nom de Georg Ohm qui a travaillé sur le comportement des conducteurs métalliques. Elle s'applique de manière satisfaisante aux conducteurs métalliques thermostatés^{[N 4]}. Lorsque la température varie, la valeur de la résistance varie également de manière plus ou moins simple, ce qui impose d'introduire des termes correctifs. Par convention, on conserve la loi et on introduit les termes correctifs dans la valeur de la résistance du conducteur.

La loi précédente se généralise au cas des courants sinusoïdaux en utilisant les notations complexes. On note U et I respectivement la tension et le courant complexes. La loi d'Ohm s'écrit alors :

${\displaystyle {\underline {U}}={\underline {Z}}\cdot {\underline {I}}}$

où Z est l'impédance complexe du dipôle considéré, qui peut être constitué de dipôles linéaires (résistances, condensateurs et inductances).

Par application de la loi des mailles,

${\displaystyle u(t)=R\;i(t)+L\,{\frac {\mathrm {d} i}{\mathrm {d} t}}+{\frac {1}{C}}\int _{}i\,\mathrm {d} t.}$

Avec :

• R la résistance du circuit, en ohms (Ω) ;
• L l'inductance de la bobine, en henrys (H) ;
• C la capacité électrique du condensateur, en farads (F).

D'un point de vue local, c'est-à-dire mésoscopique, la loi (locale) d'Ohm s'énonce en disant que la mobilité des porteurs de charge est indépendante de ${\displaystyle \left\|{\vec {E}}\right\|}$.

À noter que la loi d'Ohm doit respecter certaines conditions :

• l'homogénéité et l'isotropie du milieu ;
• la grandeur considérée ne doit pas varier trop rapidement dans le temps.

Si on note μ la mobilité des porteurs de charge, leur vitesse s'écrit alors ${\displaystyle {\vec {v}}=\pm \,\mu {\vec {E}}}$ (la direction du mouvement dépend du signe des porteurs) ; la densité de courant ${\displaystyle {\vec {\jmath }}}$ associée à une densité de porteurs n vaut quant à elle :

${\displaystyle {\vec {\jmath }}=q\,n\,{\vec {v}}=q\,n\,\mu \,{\vec {E}}}$,

où q est la charge électrique du porteur (en valeur absolue)^[5].

On note σ = q n μ la conductivité électrique du matériau (pour un seul type de porteur).

On a alors la loi locale d'Ohm pour un seul type de porteur :

${\displaystyle {\vec {\jmath }}=\sigma \,{\vec {E}}}$.

Si on a plusieurs types de porteurs, comme les électrons et les trous dans un semi-conducteur ou des ions différents dans un électrolyte, la densité de courant devient :

${\displaystyle {\vec {\jmath }}=\sum _{k}n_{k}q_{k}{\vec {v}}_{k}}$,

avec ${\displaystyle {\vec {v}}_{k}=\mu _{k}{\vec {E}}}$,

donc ${\displaystyle {\vec {\jmath }}=\left(\sum _{k}n_{k}\,q_{k}\,\mu _{k}\right){\vec {E}}}$.

On a alors la conductivité totale :

${\displaystyle \sigma =\sum _{k}n_{k}\,q_{k}\,\mu _{k}}$.

Voir aussi Loi de Nernst-Einstein.

Considérons une portion de conducteur d'un point A à un point B et de section droite S, on a alors la différence de potentiel qui vaut :

${\displaystyle V_{A}-V_{B}=\int _{A}^{B}{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}}$

et l'intensité :

${\displaystyle i=\iint _{S}{\vec {\jmath }}\cdot \mathrm {d} {\vec {S}}=\iint _{S}\sigma {\vec {E}}\cdot \mathrm {d} {\vec {S}}=\sigma \iint _{S}{\vec {E}}\cdot \mathrm {d} {\vec {S}}}$.

Multiplions par une constante la différence de potentiel V_A – V_B, alors les conditions aux limites sont inchangées ainsi que les lignes de champ de ${\displaystyle {\vec {E}}}$, et l'expression ${\textstyle \iint _{S}{\vec {E}}\cdot \mathrm {d} {\vec {S}}}$ est multipliée par la même constante. Par conséquent le rapport (V_A – V_B)/i est indépendant de cette constante, c'est une « constante » (il dépend quand même de divers paramètres tels la température) appelée résistance électrique et notée R. Elle se calcule comme suit :

${\displaystyle R={\frac {V_{A}-V_{B}}{i}}={\frac {\displaystyle \int _{A}^{B}{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}}{\displaystyle \sigma \iint _{S}{\vec {E}}\cdot \mathrm {d} {\vec {S}}}}}$

Cette formule permet de calculer la résistance de diverses géométries de matériaux (filiforme, cylindrique, sphérique, etc.).

• (fr) La loi d'Ohm (Electro-Robot)

• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Den Store Danske Encyklopædi
  • Gran Enciclopèdia Catalana
  • Internetowa encyklopedia PWN
  • Store norske leksikon
• Notices d'autorité :

  • LCCN
  • GND
  • Israël

• Portail de la physique
• Portail de l’électricité et de l’électronique