Punto singular

Un punto singular de una función es un punto donde la función es continua pero la derivada en dicho punto es discontinua^[1]​^[2]​ (más exactamente tiene una discontinuidad no evitable de primera especie).

1. ${\displaystyle \lim _{x\to a}f(x)=f(a)}$, función continua.
2. ${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}\neq \lim _{x\to a^{+}}{\cfrac {dy}{dx}}}$, no derivable.

Los puntos singulares son los únicos puntos en donde una función es continua, pero no puede trazarse una recta tangente a la función en dicho punto.

En un punto singular, esto no se cumple, las derivadas no laterales forman un ángulo no llano lo que le da el nombre a este tipo de punto, también se denominan puntos angulosos. Además, como consecuencia, no existe la normal en este punto. Además existen funciones tales que todos sus puntos son angulosos, o más exactamente donde no existe la derivada en ningún punto a pesar de que su grafo es una curva continua, uno de los primeros ejemplos de este tipo de funciones lo constituyó la función de Weierstrass:

${\displaystyle f(x)=\sum _{n=0}^{\infty }a^{n}\cos(b^{n}\pi x),}$

siendo los números reales a y b tales que:

${\displaystyle ab>1+{\frac {3}{2}}\pi .}$

Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}=-\infty }$

Función creciente para x < a.

Función decreciente para x > a.

Para x < a es Función convexa.

Para x > a es Función convexa.

Para x = a máximo relativo.

Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}<0}$

Función creciente para x < a.

Función decreciente para x > a.

Para x < a es Función convexa.

Para x > a es Función cóncava.

Para x = a máximo relativo.

Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}<0}$

Función creciente para x < a.

Función decreciente para x > a.

Para x < a es Función convexa.

Para x > a es Función cóncava..

Para x = a máximo relativo.

Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}=0}$

Función creciente para x < a.

Función decreciente para x > a.

Para x < a es Función convexa.

Para x > a es Función cóncava..

Para x = a máximo relativo.

Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}=0}$

Función creciente para x < a.

Función creciente para x > a.

Para x < a es Función convexa.

Para x > a es Función convexa.

Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}>0}$

Función creciente para x < a.

Función creciente para x > a.

Para x < a es Función convexa.

Para x > a es Función cóncava.

Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}>0}$

Función creciente para x < a.

Función creciente para x > a.

Para x < a es Función convexa.

Para x > a es Función convexa.

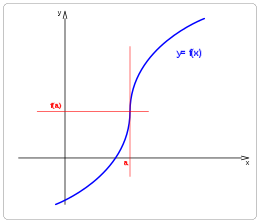
Función continua y no derivable en a

${\displaystyle \lim _{x\to a}f(x)=f(a)}$

${\displaystyle \lim _{x\to a^{-}}{\cfrac {dy}{dx}}=\infty }$

${\displaystyle \lim _{x\to a^{+}}{\cfrac {dy}{dx}}=\infty }$

Función creciente para x < a.

Función creciente para x > a.

Para x < a es Función convexa.

Para x > a es Función cóncava.

Para x = a es Punto de inflexión.

• Punto singular de una curva
• Punto crítico
• Punto estacionario
• Punto de inflexión
• Extremos de una función
• Singularidad matemática
• Clasificación de discontinuidades
• Criterio de la primera derivada
• Criterio de la segunda derivada
• Criterio de la tercera derivada
• Criterio de la derivada de mayor orden
• Punto de silla

1. Barrios García, Javier A; Carrillo Fernández, Marianela (2005). Análisis de funciones en economía y empresa. Díaz de Santos. p. 80. ISBN 84-7978-660-4.