Punto de silla

Un punto de silla o punto de ensilladura es el punto sobre una superficie en el que la pendiente es cero pero no se trata de un extremo local (máximo o mínimo). El nombre proviene de que en el ejemplo prototípico la superficie en torno al punto de silla se parece a una silla de montar a caballo.

Un ejemplo de punto de silla es un punto crítico donde la elevación es máxima en una dirección y mínima en la dirección perpendicular. Esto ocurre, por ejemplo, con el punto ${\displaystyle (0,0)}$ de la función ${\displaystyle f(x,y)=x^{2}-y^{2}}$. Sin embargo, no todos los puntos de silla son de este tipo. Por ejemplo, la función ${\displaystyle f(x,y)=x^{2}+y^{3}}$ tiene un punto de silla en (0,0), pero no tiene máximo local en ninguna dirección por el origen.

Consideremos una función diferenciable de ${\displaystyle n}$ variables: ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$. Decimos que ${\displaystyle f}$ tiene un punto de silla en ${\displaystyle {\hat {x}}=(x_{1},\ldots ,x_{n})}$, si se cumple:

1. ${\displaystyle f}$ tiene un punto crítico en ${\displaystyle {\hat {x}}}$. Es decir que el gradiente es nulo en dicho punto: ${\displaystyle \nabla f({\hat {x}})={\vec {0}}}$.
2. ${\displaystyle f}$ no tiene máximo ni mínimo local en ${\displaystyle {\hat {x}}}$. Esto equivale a decir que: para toda bola centrada en ${\displaystyle {\hat {x}}}$, existe un punto ${\displaystyle y}$ de la bola donde ${\displaystyle f(y)>f({\hat {x}})}$, y otro punto ${\displaystyle z}$ de la bola donde ${\displaystyle f(z)<f({\hat {x}})}$.

El ejemplo clásico es la llamada silla de montar, o Paraboloide hiperbólico, que se obtiene a partir de la función ${\displaystyle f(x,y)=x^{2}-y^{2}}$. En este caso el gradiente es: ${\displaystyle \nabla f(x,y)=(2x,-2y)}$. Este se anula solamente en el origen ${\displaystyle (0,0)}$. Es decir que la función tiene un único punto crítico. Veamos que este es un punto de silla, usando la definición anterior.

Los valores de la función en el eje ${\displaystyle x}$, son: ${\displaystyle f(x,0)=x^{2}>0}$. Por otro lado, los valores de la función en el eje ${\displaystyle y}$, son: ${\displaystyle f(0,y)=-y^{2}<0}$. Por lo tanto, en cualquier bola centrada en el origen, existe al menos un punto de la bola donde la función es positiva y otro donde es negativa. Como además ${\displaystyle f(0,0)=0}$, se cumple la definición de punto de silla.

Notar que, si restringimos la función ${\displaystyle f}$ al eje ${\displaystyle x}$, se obtiene la función de una variable ${\displaystyle x^{2}}$. Esta tiene un mínimo local en ${\displaystyle x=0}$, por lo que ${\displaystyle f}$ tiene un mínimo local en la dirección del eje x. En forma similar, al restringir ${\displaystyle f}$ al eje ${\displaystyle y}$, se observa que esta tiene un máximo local en la dirección del eje ${\displaystyle y}$. Esto implica que ${\displaystyle f}$ no tiene mínimo ni máximo local en ${\displaystyle (0,0)}$ (como función de dos variables). Por lo tanto, se concluye que el punto crítico ${\displaystyle (0,0)}$ es un punto de silla. Sin embargo, como se dijo al inicio, no todos los puntos de silla son de esta forma, con un máximo en una dirección y un mínimo en otra.

En consonancia con su definición, el punto de ensilladura es el más elevado que permite conectar los dos dominios altos adyacentes y es también el paso más bajo que comunica los dos dominios adyacentes que quedan por debajo. Otra propiedad de estos puntos es que por ellos pasa la curva de nivel más profunda que conecta dos dominios elevados, que determina la elevación a la que hay que descender para caminar de una montaña a otra. Por un punto de ensilladura pasa también el camino más bajo que cruza entre dos máximos de la superficie (dos montañas).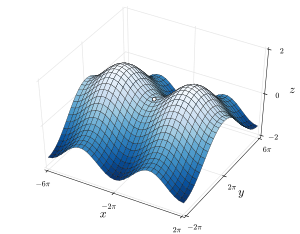

Al describir el relieve terrestre se usan dos términos equivalentes: collado de montaña (equivalente continental del umbral) y umbral submarino. Un ejemplo es el Umbral de Camarinal, que separa el Océano Atlántico del Mar Mediterráneo. Por definición, los lagos tienen su desaguadero en un punto de silla de la topografía.

• Punto de inflexión: Es el punto donde la función pasa de cóncava a convexa, o viceversa.

• Silla de mono: Un tipo particular de punto de silla.

• Wikimedia Commons alberga una galería multimedia sobre Punto de silla.
• Apuntes de análisis matemático Archivado el 22 de julio de 2009 en Wayback Machine.