|
Lokalkonvexer RaumLokalkonvexe Räume (genauer: lokalkonvexe topologische Vektorräume) sind im mathematischen Teilgebiet der Funktionalanalysis untersuchte topologische Vektorräume mit zusätzlichen Eigenschaften. Es handelt sich dabei um topologische Vektorräume, in denen jeder Punkt über „beliebig kleine“ konvexe Umgebungen verfügt. Alternativ können lokalkonvexe Räume auch als Vektorräume definiert werden, deren Topologie durch eine Familie von Halbnormen erzeugt wird.  Ein lokalkonvexer Raum kann als eine Verallgemeinerung eines normierten Vektorraumes bzw. eines normierbaren Vektorraumes betrachtet werden, denn die Normkugeln um 0 sind konvexe Umgebungen des Nullpunktes. Geometrische DefinitionEin topologischer Vektorraum (über dem Körper der reellen Zahlen oder dem Körper der komplexen Zahlen) heißt lokalkonvex, wenn jede Nullumgebung (d. h. Umgebung des Nullpunktes) eine offene Teilmenge mit den folgenden drei Eigenschaften enthält:
Eine Teilmenge eines reellen oder komplexen Vektorraumes heißt dabei absorbierend, wenn es zu jedem Vektor in eine positive Zahl gibt, so dass für jede reelle bzw. komplexe Zahl mit ein Element von ist. Eine Teilmenge eines reellen oder komplexen Vektorraumes heißt ausgewogen, wenn zu jedem Vektor in und jeder Zahl mit der Vektor ebenfalls in liegt. Im Fall eines reellen Vektorraums bedeutet dies, dass die Strecke von nach in liegt; bei einem komplexen Vektorraum bedeutet es, dass die „Kreisscheibe“ enthält. Aufgrund dieser geometrischen Bedeutung werden solche Mengen manchmal auch kreisförmig genannt. Eine ausgewogene und konvexe Menge heißt absolutkonvexe Menge. Es stellt sich heraus, dass auf die zweite und dritte Bedingung verzichtet werden kann. Es gibt genau dann eine Nullumgebungsbasis aus konvexen, absorbierenden und ausgewogenen Mengen, wenn es eine Nullumgebungsbasis aus konvexen Mengen gibt.[1] Zwei solche Umgebungsbasen müssen natürlich nicht übereinstimmen, aber die Existenz der einen impliziert die Existenz der anderen. Definition durch HalbnormenLokalkonvexe Räume lassen sich auch durch Halbnormen-Systeme charakterisieren: Ein topologischer Vektorraum heißt lokalkonvex, wenn seine Topologie durch eine Familie von Halbnormen erzeugt wird. Eine Subbasis der Topologie bilden die offenen Kugeln
Das heißt die Topologie besteht aus offenen Mengen, welche beliebige Vereinigungen von Mengen der Form sind, wobei Die Mengen sind absolutkonvexe Nullumgebungen. Diese Initialtopologie ist per Definition gleich die gröbste Topologie, so dass alle Halbnormen aus stetig sind. Ein Netz konvergiert genau dann, wenn es bezüglich aller Halbnormen aus konvergiert, das heißt genau dann, wenn für alle Halbnormen . Ist umgekehrt eine Nullumgebungsbasis aus absolutkonvexen Mengen gegeben, so bilden die zugehörigen Minkowski-Funktionale ein definierendes Halbnormen-System. Beispiele
EigenschaftenErfüllt die Halbnormenmenge aus obiger Definition , so ist der Raum ein Hausdorff-Raum. Viele Autoren betrachten nur Hausdorff’sche lokalkonvexe Räume. Hausdorffsche lokalkonvexe Räume haben genügend viele stetige, lineare Funktionale, um Punkte zu trennen, d. h. für alle gibt es ein stetiges, lineares Funktional mit . Das zeigt sich in der Gültigkeit wichtiger Sätze wie
Die stetigen, linearen Funktionale auf einem topologischen Vektorraum V trennen genau dann die Punkte, wenn es eine gröbere Topologie auf V gibt, die V zu einem hausdorffschen lokalkonvexen Raum macht. Die Untersuchung lokalkonvexer Räume mittels stetiger, linearer Funktionale führt zu einer sehr weitreichenden Theorie, die für allgemeine topologische Vektorräume so nicht möglich ist. Es gibt topologische Vektorräume, die außer dem Nullfunktional kein weiteres stetiges, lineares Funktional besitzen. VerallgemeinerungenSpezielle Klassen lokalkonvexer Räume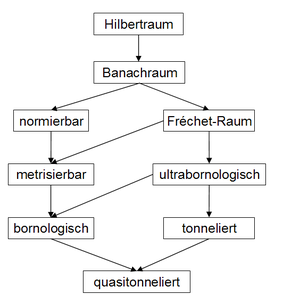 Viele Klassen lokalkonvexer Räume zeichnen sich durch die Gültigkeit bestimmter Sätze, die aus der Theorie der Banachräume oder normierten Räume bekannt sind, aus. So sind z. B. die tonnelierten Räume genau diejenigen lokalkonvexen Räume, in denen der Satz von Banach-Steinhaus noch gilt. Diese Sätze können in den entsprechenden Raumklassen in „Reinkultur“ untersucht werden, ihre Tragweite wird deutlich. Die bekanntesten dieser Raumklassen sind:
Räume differenzierbarer oder holomorpher Funktionen tragen natürliche lokalkonvexe Topologien, deren Eigenschaften zu weiteren Raumklassen Anlass geben. Die wichtigsten dieser Raumklassen, die zu einem tieferen Verständnis der lokalkonvexen Theorie führen, sind etwa
Historische BemerkungenBereits 1906 stelle M. Fréchet fest, dass der „Abschluss“ der Menge der beschränkten stetigen Funktionen auf in der Menge aller beschränkten Funktionen auf bezüglich der punktweisen Konvergenz nicht durch die Menge aller Grenzwerte von Folgen aus beschrieben werden kann. Der dazu erforderliche allgemeinere Umgebungsbegriff, wie er 1914 durch F. Hausdorff in der allgemeinen Topologie eingeführt wurde, fand in der Funktionalanalysis erstmals durch J. v. Neumann in seiner Beschreibung der schwachen bzw. starken Nullumgebungen in , Hilbertraum, Anwendung, wobei eine Verallgemeinerung auf Banachräume nicht versucht wurde. Der Umgebungsbegriff für allgemeinere Situationen findet sich bei S. Banach (1932) und Bourbaki (1938) in Untersuchungen über die schwach-*-Topologie, wobei man sich zunächst auf separable Räume beschränkte, damit die Einheitskugel im Dualraum metrisierbar ist. Obwohl die Untersuchung normierter Räume im Vordergrund stand, war damit klar, dass allgemeinere Raumklassen in natürlicher Weise auftreten. S. Banach, S. Mazur und W Orlicz betrachteten Räume, deren Topologie durch eine Folge von Halbnormen gegeben ist, und definierten den Abstand
Für die vollständigen unter diesen Räumen, die man heute Frécheträume nennt, konnte der Satz vom abgeschlossenen Graphen bewiesen werden. Dass aber auch metrisierbare Räume nicht ausreichen, zeigte die Feststellung J. v. Neumanns aus dem Jahre 1929, dass die schwache Topologie auf unendlich-dimensionalen Hilberträumen nicht metrisierbar ist. 1934 wurden von G. Köthe und O. Toeplitz neue Typen von Räumen, sogenannte Folgenräume, eingeführt und deren Dualitätstheorie im Kontext der Folgenräume entwickelt. In diesem Zusammenhang tauchte der Begriff des starken Dualraums auf. Die im Sinne der Metrik beschränkten Mengen verhielten sich nicht wie im Falle normierter Räume, es bedurfte einer topologischen Charakterisierung der Beschränktheit, wie sie in der unten zitierten Arbeit J. v. Neumanns aus dem Jahre 1935 gegeben wurde. Dieser Beschränktheitsbegriff findet sich im selben Jahr auch bei A. N. Kolmogorow bei dem Beweis der Aussage, dass ein hausdorffscher topologischer Vektorraum genau dann normierbar ist, wenn er eine beschränkte und konvexe Nullumgebung besitzt (Normierbarkeitskriterium von Kolmogorow). Von Neumanns Arbeit enthält auch erstmals die allgemeine Definition des lokalkonvexen Raums, die Äquivalenz der oben angegebenen geometrischen Definition und der Definition durch Halbnormen wird dort bewiesen. Dadurch konnten die Ideen von Köthe und Toeplitz in einem allgemeineren Rahmen durchgeführt werden. Meilensteine waren die Ergebnisse von G. Mackey aus dem Jahre 1946, siehe Satz von Mackey, Satz von Mackey-Arens, und die Untersuchungen von Tensorprodukten von A. Grothendieck aus dem Jahre 1953. Weitere Bedeutung erlangten die lokalkonvexen Räumen durch von L. Schwartz, A. Grothendieck, S. L. Sobolew, S. Bochner und anderen durchgeführten Untersuchungen in der Theorie der partiellen Differentialgleichungen und die damit einhergehende Begründung der Theorie der Distributionen. Der Satz vom Kern führte Grothendieck zum wichtigen Begriff des nuklearen Raums. Siehe auch
Literatur
Einzelnachweise
|




























![{\displaystyle {\mathcal {C}}^{\infty }([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8f12b344c668e5e1cd6504d3c302ca3dd56243f)
![{\displaystyle p_{k}(f)=\sum _{i\leq k}\max _{x\in [0,1]}|f^{(i)}(x)|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fb7c398f626edd4c37e65a970be2735e94aff4d)










