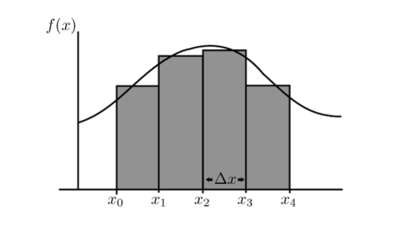
Integral de Riemann

La integral de Riemann és una operació sobre una funció contínua i limitada en un interval ${\displaystyle [a,b]}$, on ${\displaystyle a}$ i ${\displaystyle b}$ són anomenats extrems de la integració. L'operació consisteix a trobar el límit de la suma de productes entre el valor de la funció en un punt ${\displaystyle x_{i}^{*}}$ i l'amplada ${\displaystyle \Delta x}$ del subinterval que conté al punt.

${\displaystyle \lim _{n\to \infty }\sum _{i=0}^{n-1}f(x_{i}^{*})\Delta x_{i-1}}$

Normalment es nota com:

${\displaystyle \int _{a}^{b}f(x)dx}$

El símbol ${\displaystyle \int }$ és una "S" deformada. En el cas en què la funció ${\displaystyle f}$ tingui diverses variables, el ${\displaystyle dx}$ especifica la variable d'integració. Si la variable d'integració i l'interval d'integració són coneguts, la notació es pot simplificar com ${\displaystyle \int f}$.

Algunes funcions no són clarament integrables per Riemmann, però en general les interaccions dels límits amb la integral de Riemmann són difícils d'estudiar.

La integral de Lebesgue millora aquesta teoria i permet obtenir una millor varietat de funcions integrables, així com descriure millor les interaccions dels límits amb la integral.

Històricament, Riemann va concebre aquesta teoria de la integració, i va proporcionar algunes idees per al teorema fonamental del càlcul. La teoria de la integració de Lebesgue va arribar molt més tard, quan els punts dèbils de la integral de Riemann es comprenien millor.

En anàlisi de variable real, la integral de Riemann és una forma simple de definir la integral d'una funció sobre un interval com l'àrea sota la corba de la funció.

Sigui ${\displaystyle f}$ una funció amb valors reals definida sobre l'interval ${\displaystyle [a,b]}$, tal que per tot ${\displaystyle x}$, ${\displaystyle f(x)\geq 0}$. Sigui ${\displaystyle S=S_{f}=\{(x,y)|0\leq y\leq f(x)\}}$ la regió del pla delimitada per la corba corresponent a la funció ${\displaystyle f}$, l'eix de les abscisses i les rectes verticals de les equacions ${\displaystyle x=a}$ i ${\displaystyle x=b}$. Ens interessa mesurar l'àrea del domini S, si és que es pot mesurar.

Per obtenir una aproximació de l'àrea tancada sota una corba, aquesta es pot dividir en rectangles com indica la figura següent:

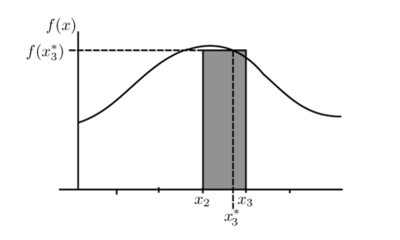
L'àrea de cada rectangle, és el producte de la funció en un punt, per l'amplada de l'interval:

Quan s'augmenta el nombre de rectangles s'obté una millor aproximació:

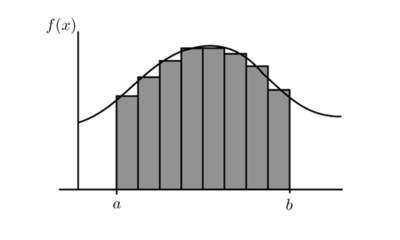
La idea fonamental de la teoria de la integració de Riemann és la d'utilitzar aproximacions de l'àrea del domini S. Es determinarà una àrea aproximada que se sàpiga que és inferior a l'àrea del domini S, i es buscarà una altra àrea aproximada que se sàpiga que és major que l'àrea de S. Si aquestes aproximacions poden fer-se de manera que la diferència entre ambdues àrees sigui arbitràriament petita, llavors podem obtenir l'àrea del domini S. Per tant, el límit de l'àrea per a infinits rectangles és l'àrea compresa sota la corba.

• Integral de Darboux