|
Gabungan (teori himpunan)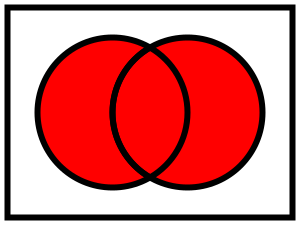 Dalam teori himpunan, gabungan (bahasa Inggris: union) dari koleksi himpunan adalah himpunan semua anggota dalam koleksi.[1] Gabungan merupakan salah satu operasi dasar, yang dapat menggabungkan atau mengaitkan anggota himpunan ke anggota himpunan lain. Gabungan dilambangkan dengan ∪. Untuk penjelasan tentang penggunaan simbol lebih lanjut, lihat tabel dari simbol matematika Gabungan dari dua himpunanGabungan dari himpunan dan adalah himpunan anggota yang berada di , atau , atau bahkan kedua-duanya.[2] Gabungan dari dua himpunan tersebut dituliskan dalam notasi ungkapan himpunan.[3]Sebagai contoh, jika dan , maka . Contoh yang lebih rumit (meliputi dua himpunan tak terhingga) adalahː Contoh lainnya, 9 tidak termasuk dalam gabungan dari himpunan bilangan prima dan juga himpunan dari bilangan genap , sebab 9 bukanlah bilangan prima ataupun bilangan genap. Himpunan tidak mempunyai anggota identik yang muncul lebih dari satu kali,[3] karena itu gabungan dari dan adalah . Banyaknya kemunculan anggota yang identik tersebut tidak mempengaruhi kardinalitas himpunan ataupun isi himpunannya. Sifat aljabarGabungan biner adalah operasi asosiatif. Hal ini berarti bahwa untuk setiap himpunan , , dan , berlaku Pada rumus di atas, tanda kurung dapat dihilangkan dalam rangka untuk menghindari keambiguan, sehingga dapat ditulis juga sebagai . Gabungan merupakan operasi komutatif, sehingga himpunan bisa ditulis dalam setiap urutan.[4] Himpunan kosong adalah anggota identitas untuk operasi gabungan, dalam artian bahwa , untuk setiap himpunan . Secara analogi, semua sifat-sifat tersebut diikuti dari logika disjungsi. Adapun sifat aljabar lainnya, yakni irisan distribusi atas gabungandan gabungan distribusi atas irisan[5]Himpunan kuasa dari himpunan , beserta operasi-operasinya, seperti gabungan, irisan, dan komplemen, merupakan aljabar Boole. Dalam aljabar Boole, gabungan dapat dinyatakan dengan rumus yang mengandung operasi irisan dan komplemen.dengan superskrip C melambangkan komplemen dalam himpunan semesta . Gabungan terhingga Beberapa himpunan dapat diambil secara serentak. Sebagai contoh, gabungan dari tiga himpunan , , dan mengandung semua anggota dari , semua anggota dari , dan semua anggota dari , dan tidak ada lagi. Dengan demikian, adalah anggota dari jika dan hanya jika setidaknya ada di dalam salah satu himpunan , , dan . Gabungan terhingga adalah gabungan dari jumlah terbatas pada himpunan-himpunan; ungkapan tidak menyiratkan bahwa gabungan himpunan adalah himpunan terbatas.[6][7] Gabungan sebarangGagasan yang paling umum adalah gabungan dari koleksi himpunan sebarang, yang kadangkala disebut gabungan tak terhingga. Jika adalah himpunan atau kelas yang anggotanya ada di himpunan, maka adalah gabungan dari jika dan hanya jika setidaknya ada satu anggota dari sehingga anggota dari .[8] Ini dapat ditulis dengan menggunakan simbolGagasan ini menggolongkan bagian sebelumnya, sebagai contoh, adalah gabungan dari koleksi . Juga, jika adalah koleksi kosong, maka gabungan dari adalah himpunan kosong NotasiNotasi untuk konsep yang umum sangat bervariasi. Untuk gabungan terhingga dari himpunan , acapkali ditulis sebagai atauTerdapat bermacam-macam notasi untuk gabungan sembarang, seperti , , atau , yang mengacu pada gabungan dari koleksi , dengan adalah himpunan indeks, dan adalah himpunan untuk . Terdapat sebuah kasus bahwa untuk himpunan indeks yang merupakan himpunan bilangan asli, dapat menggunakan notasiyang mirip seperti jumlah tak terhingga dalam deret.[8] Lihat pula
Catatan
Pranala luar
|


















































