多面形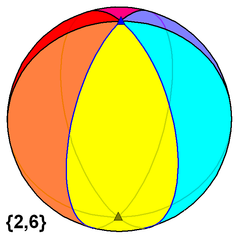

多面形

以六面形為例
類別	正多面體 球面鑲嵌
對偶多面體	多邊形二面體
數學表示法
考克斯特符號 （英语：Coxeter-Dynkin diagram）
施萊夫利符號	{2,n}
威佐夫符號 （英语：Wythoff symbol）	n | 2 2
性質
面	${\displaystyle n}$
邊	${\displaystyle n}$
頂點	${\displaystyle 2}$
歐拉特徵數	F=${\displaystyle n}$, E=${\displaystyle n}$, V=${\displaystyle 2}$ （χ=2）
組成與佈局
面的種類	n個二角形
頂點圖	2n
頂點佈局 （英语：Vertex_configuration）	2n
對稱性
對稱群	Dnh, [2,n], (*22n), order 4n
旋轉對稱群 （英語：Rotation_groups）	Dn, [2,n]+, (22n), order 2n
圖像
多邊形二面體 （對偶多面體）
註：${\displaystyle n}$為底面邊數 。
查 论 编

在幾何學中，多面形（英語：Hosohedron）是一種由月牙形或球弓形組成的球面鑲嵌，並且使得每一個月牙形或球弓形共用相同的兩個頂點。其在施萊夫利符號中用 {2, n} 表示n面形。

其亦可以視為由球面正二角形組成的球面鑲嵌圖，又稱為二角形鑲嵌或二邊形鑲嵌。

在施萊夫利符號中以{m, n}表示的正多面體，其面的個數存在下列等式：

${\displaystyle N_{2}={\frac {4n}{2m+2n-mn}}}$

自古以來大家所熟知的正多面體——柏拉圖立體是當m≥3且n≥3的整數解，限制在m≥3的狀態下，多邊形面必須至少有三條邊。

當考慮多面體為球面鑲嵌時，該限制可以放寬，因為二角形（二邊形）可以以球弓形或月牙形存在，即球面二角形具有非零面積。當m=2時則會產生一個新的無窮集合，即多面形。在球面上，所述多面體{2, n}表示當n個球弓形組合，並且具有2π/n內角。所有二角形階共用相同的兩個頂點，即每個頂點皆為所有二角形的公共頂點。

每個正多面形都是n階二邊形鑲嵌。

一個正三面形，{2,3}，以三個月牙形鑲嵌於求面表示。又稱三階二邊形鑲嵌。

一個正四面形，以四個月牙形鑲嵌於求面表示。又稱四階二邊形鑲嵌。

正多面形系列

球面鑲嵌													歐式鑲嵌 仿緊空間	雙曲鑲嵌 非緊空間
1	2	3	4	5	6	7	8	9	10	11	12	...	∞	iπ/λ
一面形	二面形	三面形	四面形	五面形	六面形	七面形	八面形	九面形	十面形	十一面形	十二面形		無限面形	超無限面形
{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}	{2,9}	{2,10}	{2,11}	{2,12}		{2,∞}	{2,iπ/λ}

英文Hosohedron一詞由考克斯特命名，其來自希臘語ὅσος (osos/hosos)，是『盡可能多』的意思，其意思為『盡可能達到很多的面的形狀^[1]』因此稱為多面形。

多維面形是多面形在高維度的類比，表示有多個維面的幾何圖形。任何正的維面形都可以以施萊夫利符號{2,p,...,q}表示

多維面形

施萊夫利 {2,p,q}	考克斯特符号（英语：Coxeter-Dynkin diagram）	胞 {2,p}π/q	面 {2}π/p,π/q	邊	頂點	頂點圖 {p,q}	對稱性	對偶多胞形
{2,3,3}		4 {2,3}π/3	6 {2}π/3,π/3	4	2	{3,3}	[2,3,3]	{3,3,2}
{2,4,3}		6 {2,4}π/3	12 {2}π/4,π/3	8	2	{4,3}	[2,4,3]	{3,4,2}
{2,3,4}		8 {2,3}π/4	12 {2}π/3,π/4	6	2	{3,4}	[2,4,3]	{4,3,2}
{2,5,3}		12 {2,5}π/3	30 {2}π/5,π/3	20	2	{5,3}	[2,5,3]	{3,5,2}
{2,3,5}		20 {2,3}π/5	30 {2}π/3,π/5	12	2	{3,5}	[2,5,3]	{5,3,2}

多香腸面形（lucanicohedron）又稱為截半多面形（rectified hosohedron）是一種半正則地區圖，源自於多面形，其結構為兩個多邊形底面以類似多邊形二面體的方式貼合，但貼合的棱處加上二角形的側面所構成的正則地區圖^[2]，名稱lucanicohedron源自於這種立體以二角形在側面循環有如香腸串一般，因此取香腸的希臘語λουκάνικο作為字首lucanico-結合多面體字尾-hedron構成的複合詞。^[3]

多香腸面形是多面形或多邊形二面體經截半變換的結果。^[4]

维基共享资源上的相关多媒体资源：多面形

• 多面體
• 多胞形
• 多胞體

• Coxeter, H.S.M; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
• 埃里克·韦斯坦因. Hosohedron. MathWorld.