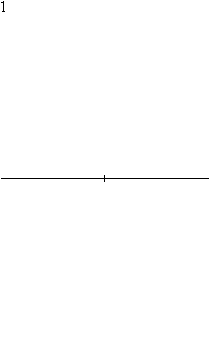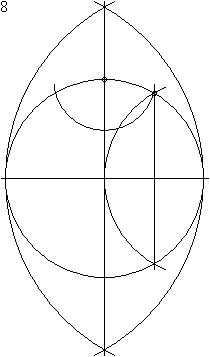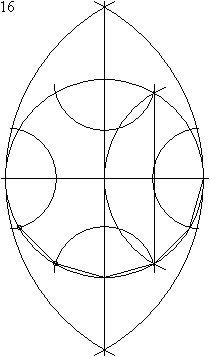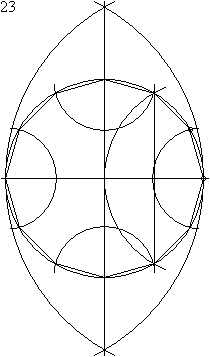在幾何學 中,十二邊形 是指有十二條邊和十二個頂點 的多邊形 [ 1] [ 2] 對稱性 最高的是正十二邊形。其他的十二邊形依照其類角的性質可以分成凸十二邊形和非凸十二邊形,其中凸十二邊形代表所有內角角度皆小於180度。非凸十二邊形可以在近一步分成凹十二邊形和星形十二邊形 ,其中星形十二邊形表示邊自我相交的十二邊形。而一般的十字形為凹十二邊形常見的一個例子。
正十二邊形是指所有邊等長、所有角等角的十二邊形,由十二條相同長度的邊和十二個相同大小的角構成,是一種正多邊形 。正十二邊形的內角是
5
π
6
{\displaystyle {\frac {5\pi }{6}}}
弧度 ,換算成角度是150度 。在施萊夫利符號 中用
{
12
}
{\displaystyle \left\{12\right\}}
頂點 的正六邊形,即截角 的正六邊形 ,因此施萊夫利符號中也可以計為
t
{
6
}
{\displaystyle t\left\{6\right\}}
正六邊形 亦可以將正三角形 透過截角變換 來構造,即切去正三角形 的三個頂點,因此正十二邊形可以視為正三角形經過2次的截角變換的結果,在施萊夫利符號中亦可以寫為
t
t
{
3
}
{\displaystyle tt\left\{3\right\}}
若已知正十二邊形的邊長a,則正十二邊形的面積 為:
A
=
3
cot
(
π
12
)
a
2
=
3
(
2
+
3
)
a
2
≃
11.19615242
a
2
{\displaystyle {\begin{aligned}A&=3\cot \left({\frac {\pi }{12}}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}\\&\simeq 11.19615242\,a^{2}\end{aligned}}}
若已知內切圓 半徑 或邊心距 為r,則其面積為:
A
=
12
tan
(
π
12
)
r
2
=
12
(
2
−
3
)
r
2
≃
3.2153903
r
2
{\displaystyle {\begin{aligned}A&=12\tan \left({\frac {\pi }{12}}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}\\&\simeq 3.2153903\,r^{2}\end{aligned}}}
若已知外接圓 半徑為R,其面積為:[ 3]
A
=
6
sin
(
π
6
)
R
2
=
3
R
2
{\displaystyle A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2}}
三国 时代数学家 刘徽 计算出半径 为
r
{\displaystyle r}
圆形 ,其内接正12边形的面积为
3
r
2
{\displaystyle 3r^{2}}
[ 4] [ 5] 面积 等于最长对角线 平方的四分之三。
十二邊形的寬度是兩個平行 邊之間的距離,正好會等於兩倍的邊心距。因此已知正十二邊形的寬度和邊長也可以求出面積:
A
=
3
a
S
{\displaystyle A=3aS}
也可以利用三角關係 進行驗證:
S
=
a
(
1
+
2
cos
30
∘
+
2
cos
60
∘
)
{\displaystyle S=a(1+2\cos {30^{\circ }}+2\cos {60^{\circ }})}
若已知外接圓 半徑R,正十二邊形的周長 為[ 6]
p
=
24
R
sin
(
π
12
)
=
12
R
2
−
3
≃
6.21165708246
R
{\displaystyle {\begin{aligned}p&=24R\sin \left({\frac {\pi }{12}}\right)=12R{\sqrt {2-{\sqrt {3}}}}\\&\simeq 6.21165708246R\end{aligned}}}
若已知邊心距r,正十二邊形的周長 為:
p
=
24
r
tan
(
π
12
)
=
24
r
(
2
−
3
)
≃
6.43078061835
r
{\displaystyle {\begin{aligned}p&=24r\tan \left({\frac {\pi }{12}}\right)=24r(2-{\sqrt {3}})\\&\simeq 6.43078061835r\end{aligned}}}
該系數是已知邊心距求面積公式中系數的兩倍[ 7]
尺規作圖 可先在圓形內製作正六邊形 ,再將各邊二等分線延伸至圓周以完成正十二邊形的頂點 。
以尺規作圖作出正12邊形。
有一些正多邊形鑲嵌圖 含有正十二邊形 :
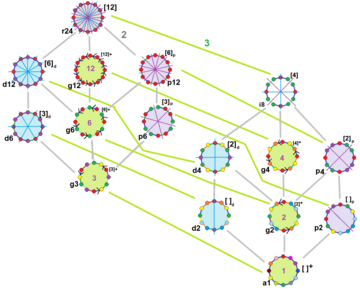
一般的十二邊形對稱性以對邊和頂點的顏色顯示。約翰·何頓·康威 以字母來標記這些形狀的對稱性。[ 11] 正十二邊形具有Dih12 對稱性,階數為24.
有15個不同的子群二面體群和環狀對稱。每個子組對稱性允許一個或多個自由不規則形式。只有G12 子群沒有自由度,但可以看作是有向邊 。
不同對稱性的十二邊形
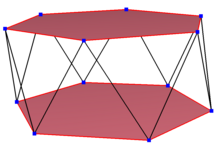
一個正扭歪十二邊形,位於六角反柱上 扭歪十二邊形,又稱不共面十二邊形,是指頂點並非完全共面的十二邊形。
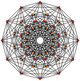
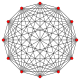
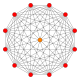
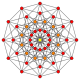
扭歪十二邊形經常出現在高維多胞體正交投影 的皮特里多邊形 。例如十一維正十二胞體的皮特里多邊形就是一個扭歪十二邊形,其具有A11 [310 ] 的考克斯特群 的對稱性[ 12]
英鎊 的新版1鎊硬幣形狀為正十二邊形。澳大利亞元 的50分硬币形狀為正十二邊形。澳門幣 五圓和二毫的形状为正十二邊形二毫 和二元 港币 的形状为正十二邊形(严格地说,是每边向内凹陷的正十二边形)嵩岳寺塔的底為正十二邊形。
^ Weisstein, Eric W. (编). Dodecagon . at MathWorld Wolfram Research, Inc. (英语) . ^ Polygons – Dodecagon . coolmath.com. [2016-08-28 ] . (原始内容存档 于2016-08-28). ^ 柯謝克 Kürschák's Dodecagon . the Wolfram Demonstration Project. [2016-08-25 ] . (原始内容 存档于2018-07-31). ^ 《九章算術 》卷第一 - 大哉言數
^ Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 56-57 and 137, 1991. ISBN 978-0140118131
^ Plane Geometry: Experiment, Classification, Discovery, Application by Clarence Addison Willis B., (1922) Blakiston's Son & Company, p. 249 [1] (页面存档备份 ,存于互联网档案馆 )^ Elements of geometry
by John Playfair, William Wallace, John Davidsons, (1814) Bell & Bradfute, p. 243 [2] (页面存档备份 ,存于互联网档案馆 )^ " Doin' Da' Dodeca'" [2017-06-08 ] . (原始内容存档 于2016-09-17). ^ Chavey, D. Tilings by Regular Polygons—II: A Catalog of Tilings . Computers & Mathematics with Applications. 1989, 17 : 147–165 [2016-08-28 ] . doi:10.1016/0898-1221(89)90156-9 存档 于2016-06-16). ^ Uniform Tilings . [2016-08-28 ] . (原始内容 存档于2006-09-09). ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
^ Davis, Michael W., The Geometry and Topology of Coxeter Groups (PDF) , 2007 [2016-08-27 ] , ISBN 978-0-691-13138-2Zbl 1142.20020 原始内容 (PDF) 存档于2011-10-09)