ความถี่เชิงมุม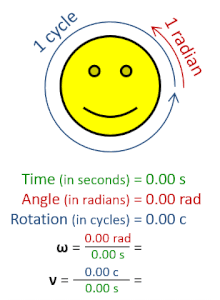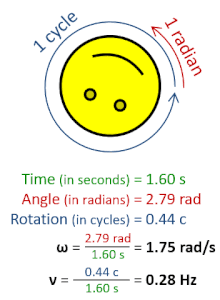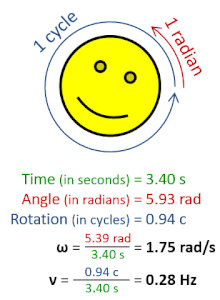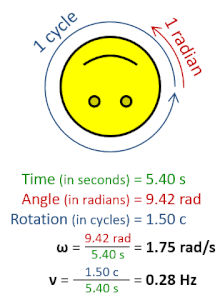

ในทางฟิสิกส์ ความถี่เชิงมุม (อังกฤษ: Angular frequency, สัญลักษณ์: ω) รวมถึง ความเร็วเชิงมุม (อังกฤษ: Angular speed) เป็นปริมาณสเกลาร์ของอัตราการหมุน โดยมีความหมายคือ การกระจัดเชิงมุมต่อหนึ่งหน่วยเวลา (เช่น การหมุน) หรือ อัตราการเปลี่ยนแปลงของเฟสในคลื่นรูปไซน์ (เช่น การแกว่งและคลื่น) หรือ อัตราการเปลี่ยนแปลงของอาร์กิวเมนต์ของฟังก์ชันไซน์^[1]

หนึ่งรอบการหมุนนั้นเท่ากับ 2π เรเดียน ฉะนั้น^[1][2]

$${\displaystyle \omega ={\frac {2\pi }{T}}={2\pi f},}$$ เมื่อ :

• ω คือ ความถี่เชิงมุม (หน่วย เรเดียนต่อวินาที)
• T คือ คาบ (หน่วย วินาที)
• f คือ ความถี่ (หน่วย เฮิรตซ์) (บางครั้งใช้เป็น ν)

ในหน่วย SI โดยปกติแล้วความถี่เชิงมุมจะมีหน่วยเป็น เรเดียนต่อวินาที แม้บางครั้งจะไม่แสดงค่าของการหมุนก็ตาม หากมองในมุมมองของการวิเคราะห์เชิงมิติแล้วนั้น การใช้หน่วยเป็น เฮิรตซ์ (Hz) ก็ถือว่าถูกต้องเช่นกัน หากแต่ตามธรรมเนียม Hz จะใช้กับความถี่ f เท่านั้นและแทบจะไม่ใช้กับความถี่เชิงมุม ω เลย โดยที่คงไว้แบบนี้ก็เพื่อป้องกันการสับสน^[3]เมื่อนำมาใช้กับความถี่หรือค่าคงตัวของพลังค์ เพราะว่าหน่วยของการวัดเชิงมุม (รอบหรือเรเดียน) นั้นถูกละเว้นในระบบ SI นั่นเอง^[4][5]

ในการประมวลผลสัญญาณดิจิทัล ความถี่เชิงมุมนั้นอาจถูกทำให้เป็นมาตรฐานโดยอัตราการสุ่มตัวอย่าง เพื่อให้ได้ผลเป็นความถี่ปกติ

ในการหมุนหรือการโคจรของวัตถุ จะมีค่าความสัมพันธ์ระหว่าง ระยะห่างจากแกน (${\displaystyle r}$), ความเร็วในแนวสัมผัส (${\displaystyle v}$) และ ความถี่เชิงมุมของการหมุน ในระหว่าง 1 คาบ (${\displaystyle T}$) วัตถุเคลื่อนที่เป็นวงกลมได้ระยะทาง ${\displaystyle vT}$ ซึ่งระยะทางนั้นจะเท่ากับเส้นรอบวงที่ถูกพาดผ่านโดยวัตถุนั้น (${\displaystyle 2\pi r}$) ทำให้ปริมาณสองปริมาณนั้นมีค่าเท่ากัน เมื่อนำความสัมพันธ์ของคาบกับความถี่เชิงมุมมาคิด เราจะได้:${\displaystyle \omega =v/r.}$

1. ↑ ^{1.0 1.1} Cummings, Karen; Halliday, David (2007). Understanding physics. New Delhi: John Wiley & Sons Inc., authorized reprint to Wiley – India. pp. 449, 484, 485, 487. ISBN 978-81-265-0882-2.(UP1)
2. ↑ Holzner, Steven (2006). Physics for Dummies. Hoboken, New Jersey: Wiley Publishing Inc. pp. 201. ISBN 978-0-7645-5433-9. angular frequency.
3. ↑ Lerner, Lawrence S. (1996-01-01). Physics for scientists and engineers. p. 145. ISBN 978-0-86720-479-7.
4. ↑ Mohr, J. C.; Phillips, W. D. (2015). "Dimensionless Units in the SI". Metrologia. 52 (1): 40–47. arXiv:1409.2794. Bibcode:2015Metro..52...40M. doi:10.1088/0026-1394/52/1/40. S2CID 3328342.
5. ↑ "SI units need reform to avoid confusion". Editorial. Nature. 548 (7666): 135. 7 August 2011. doi:10.1038/548135b. PMID 28796224.