|
Lewis Fry Richardson
Lewis Fry Richardson (født 11. oktober 1881, død 30. september 1953) var en engelsk matematiker, fysiker, meteorolog, psykolog og pasifist. Han var en foregangsmann innen moderne matematiske teknikker for værmelding, og for bruken av lignende teknikker i studiet av årsakene til kriger og hvordan de kan forebygges. Han er også kjent for sitt pionerarbeid innen fraktaler. Familie og utdanningLewis Fry Richardson var den yngste av syv barn av foreldrene Catherine Fry (1838–1919) og David Richardson (1835–1913). De var en velstående kvekerfamilie, og David Richardson drev en fremgangsrik virksomhet innen garveri- og lærbransjen.[3] Da han var tolv ble han sendt til Bootham skole i York, en internatskole for kvekere, hvor han fikk en utmerket utdannelse innen vitenskap, noe som stimulerte en aktiv interesse for naturhistorie. I 1898 fortsatte han til Durham College of Science (nå Universitetet i Newcastle) hvor han studerte matematisk fysikk, kjemi, botanikk og zoologi. To år senere fikk han et stipendiat til King's College i Cambridge, hvor han ble uteksaminert med toppkarakterer innen naturvitenskap i 1903.[3] I 1909 giftet han seg med Dorothy Garnett (1885–1956), datter av matematikeren og fysikeren William Garnett.[4] På grunn av inkompatible blodtyper kunne de ikke få barn, men de adopterte to sønner og en datter mellom 1920 og 1927.[5] KarriereRichardsons yrkeskarriere reflekterer hans uensartede interesser:[6]
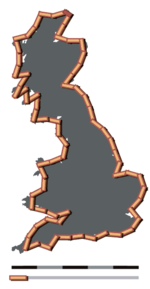
I 1926 ble han innvalgt som medlem av Royal Society[7] VærvarslingSom matematiker og fysiker viet han seg til spørsmålet om hvorvidt man kunne lage meteorologiske varsler ved hjelp av matematisk modeller basert på differensialligninger. Med dette for øye utviklet han metoder som i nyere tid har fått stor betydning ved simulering av komplekse fenomener ved hjelp av parallell databehandling. Ved dette blir området hvor hendelsen finner sted inndelt i flere mindre seksjoner, og ideen er å beregne tilstanden til hver seksjon gjennom en enkel modell. I neste steg blir så resultatene fra de enkelte seksjonene sett i sammenheng med resultatet fra naboseksjonene. På denne måten blir det svært komplekse simuleringsproblemet delt opp i en mengde mindre problemer, som i stor grad kan løses uavhengig av hverandre. I dag blir beregningene gjort med datamaskiner, men dette var ikke tilgjengelig da Richardson i 1922 publiserte Weather Prediction by Numerical Process, og selv relativt enkle simuleringer ville ha krevd en stort antall personer som arbeidet med papir og blyant. Han var også interessert i atmosfærisk turbulens og utførte mange eksperimenter innen dette feltet. Richardson-tallet, et dimensjonsløst parameter innen turbulensteori, er oppkalt etter han. PasifismeRichardsons kvekertro medførte en lidenskapelig pasifisme, som fritok han fra militærtjeneste under første verdenskrig som militærnekter, selv om dette også diskvalifiserte han fra å inneha akademiske embeter for fremtiden. Richardson arbeidet fra 1916 til 1919 for en frivillig ambulansetjeneste av kvekere (Friends' Ambulance Unit) tilknyttet Den 16. franske infanteridivisjon. I 1920 ble det meteorologiske instituttet (Met Office) han arbeidet for underlagt det britiske Air Ministry (som kontrollerte Royal Air Force). Han ble like etter kontaktet av militære representanter, som ønsket å bruke hans meteorologiske modeller i forbindelse med spredning av giftgass i atmosfæren. Richardson nektet, sa opp sin stilling, og avsluttet alt arbeid innen dette feltet og ødela resultater som han ennå ikke hadde publisert.[8] Etter dette fortsatte han med en karriere i utkanten av den akademiske verden, før han i 1940 trakk seg tilbake for å utforske sine egne ideer. Matematisk analyse av krigRichardson benyttet også sine matematiske evner i tjeneste for sine pasifistiske prinsipper, spesielt innen studier av årsakene til internasjonale konflikter. Av denne grunn anses han i dag som en av grunnleggerne (sammen med Quincy Wright og Pitirim Sorokin, samt andre som Kenneth Boulding, Anatol Rapaport og Adam Curle) av vitenskapelig konfliktanalyse; et interdisiplinært felt innen kvantitativ og matematisk sosial vitenskap, dedikert til systematisk undersøkelse av årsakene til krig og betingelser for fred. Som han hadde gjort med været analyserte han krig hovedsakelig gjennom bruk av differensialligninger og sannsynlighetsteori. Når han vurderte bevæpningen av to stater antok Richardson et idealisert system av ligninger hvorved økningen i en stats våpenmakt er direkte proporsjonalt med våpenmengden som dens rival har, og også med hvor sterkt stridsspørsmålene ovenfor rivalen føles, og negativt proporsjonalt med mengden av våpen som staten selv )allerede har. Løsningen av dette systemet av ligninger gjør det mulig å trekke innsiktsfulle konklusjoner vedrørende karakteren og stabiliteten (eller ustabiliteten), til forskjellige hypotetiske betingelser som kan oppstå mellom stater. I Arms and Insecurity (1949), og Statistics of Deadly Quarrels (1950), søkte han å statistisk analysere årsakene til krig. Faktorer han vurderte var blant annet økonomi, språk og religion. I forordet til den siste boka skrev han: «Det foregår i verden mye brilliant, intelligent politisk diskusjon som ikke fører til noen faste løsninger. Mitt siktemål har vært et annet: nemlig å undersøke noen forestillinger ved hjelp av kvantitative teknikker i håp om å komme fram til et pålitelig svar.» Forskning om lengden på kystlinjer og grenserUnder sine studier av årsakene til krig mellom to land, bestemte Richardson seg for å undersøke hvorvidt det var en sammenheng mellom sannsynligheten for at to land skulle gå til krig, og lengden på deres felles grense. Mens han samlet inn data, innså han at det var betydelig variasjon i de oppgitte lengdene på internasjonale grenser i de forskjellige kildene. For eksempel var grensen mellom Spania og Portugal oppgitt å være enten 987 eller 1214 km, og grensen mellom Nederland og Belgia enten 380 eller 449 km. Som en del av sitt forskningsarbeid undersøkte Richardson hvordan den oppmålte lengden på en grense endres når måleenheten endres. Han publiserte empirisk statistikk som indikerte en antatt sammenheng. Dette forskningsarbeidet ble sitert av matematikeren Benoît Mandelbrot i hans avhandling fra 1967: How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Anta at kysten av Storbritannia blir målt med en 200 km lang linjal, under forutsetning at begge endene av linjalen må berøre kysten. Kutt nå linjalen i to og gjenta målingen, og gjenta deretter en gang til: Legg merke til at desto kortere linjalen er, desto lengre blir resultatet. Det kunne antas at disse verdiene ville konvergere til et endelig tall som uttrykte kystens «egentlige» lengde. Richardson viste imidlertid at den oppmålte lengden til kystlinjer og andre naturlige former ser ut til å øke uten grense etterhvert som måleenheten gjøres mindre.[9] Dette er i dag kjent som Richardson-effekten. På den tid ble Richardsons forskning ignorert av den vitenskapelige verden. I dag blir den imidlertid sett på som et element i framveksten i studiet av fraktaler. Bibliografi(ufullstendig)
Referanser
Litteratur
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||