水流モデル

水流モデル (すいりゅうモデル、英: electronic–hydraulic analogy) は、金属のような導体に電圧をかけた際に発生する、電子の流れを説明する時に使用されているアナロジーである。電流は目に見えず、電気回路中で起こる過程を説明しづらいため、各種電子部品が電流に対して果たす役割を水流で表現するものである。電気は元来、ある種類の流体として理解されており、電気を特徴付ける各種の量の名前も「電流」など、流体を想起するものになっていることがある。

このモデルを構成する方法は1通りではない。大別して重力によって圧力を生み出すモデルと、ポンプによって圧力を生み出すモデルがある。

重力における圧力では、大きな水タンクを複数用意して、片方を高所におくか、水位を異なるようにするなどして、水頭の位置エネルギーを圧力元とする。このモデルでは電位が重力ポテンシャルと等価である強みがある。

第2の方法は、圧力を生み出すポンプを用いて、重力は用いないものである。こちらは回路の電源が明確になり、回路を完成させられる点において有利である。この方法については、次節で検討する。

その他の方法でも、流体の流れを扱う方程式と電荷の流れを扱う方程式の類似性に準拠している。流量と圧力は定常の場合でも非定常の場合でも、水流のインピーダンスから計算できる^[1][2]。水流のインピーダンスは、水圧と体積流量の比として定義される。このとき、圧力と流量はフェーザ表示で扱われるため、大きさと共に位相も持つ^[3]。

音響学においては、水流モデルの変種として、圧力と音速の関係を音響インピーダンスと定義するものが使われている。この方法では、穴を1つ開けた大きなキャビティ（空洞）はコンデンサに類似する。圧力が時間に依存して大気圧と異なる場合、キャビティに圧縮エネルギーが蓄えられる。穴（あるいは長い管）は空気の流れの運動エネルギーを蓄えるインダクタに類似する^[4]。

回路によるモデルは、磁気ミラー中でのプラズマの流体力学的不安定性のフィードバック安定化をモデル化するためにも使用された^[5]。この応用は、極板への電圧印加によってプラズマを中心に維持するためのものである。乱流および非線形効果が存在していることを除けば、プラズマは（アナロジーではなく）本当の電気回路を作ると考えられる。

一般に電位は水頭に相当するが、このモデルでは、水が水平に流れることを仮定するため重力は無視でき、電位は圧力に相当する。電圧（電圧降下又は電位差）は、2点間の圧力の差である。電位、電圧は、通常ボルト単位で表す。

電流は流量、つまり単位時間当たりに流れる水の体積に相当する。通常アンペア単位で表す。

電荷は水の量に相当する。

• 
  導線：単純なパイプ。
• 
  抵抗：細くなったパイプ。
• 
  キルヒホッフの第1法則における節点：T字管。

太いパイプに水を満たしたものは導線に相当する。導線に例える場合は、パイプの両端にキャップがついていると考える。導線の片方の端を回路に接続することは、パイプの片方の端のキャップを外して別のパイプに接続したことに相当する。高圧電源に接続したような少数の例外を除き、片方の端だけ導線を回路に接続しても何も起こらない。他方の端にはキャップがついたままなので、回路には何も流れない。

抵抗は細くなったパイプに相当する。細いパイプでは、同量の水を通すにもより強い圧力を必要とする。いかなる導線にも電流に対する抵抗があるように、すべてのパイプもまた、水が流れる時に抵抗がある。

キルヒホッフの法則におけるノード（接点）はパイプの分岐に相当する。分岐に正味で流入した量と同じだけ流出がある。

• 
  コンデンサ：柔軟なダイアフラムで仕切られたパイプ。
• 
  コイル：流れの中に設けられた重い水車もしくはタービン。
• 
  電圧源（電流源）：フィードバック制御されたポンプ。

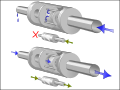
水流モデルにおけるコンデンサは、両端がそれぞれパイプにつながったタンクで、タンク内がゴムシートで分割されている（油圧アキュムレータ）状況に相当する^[6]。水が片方のパイプから入り込むと別の側のパイプから出ていくことになるが、ゴムシートを水が貫くことはない。ゴムが伸びることによってエネルギーを蓄えることができる。より多くの水がコンデンサを「通る」につれて、コンデンサの流入側圧力は高まる。このように、コンデンサでは電流が電圧を生み出すといえる。流入側の内圧が印加された圧力と等しくなるにつれて電流は減っていく。このようにして、コンデンサは一定の圧力やゆっくり変化する低周波圧力を通過させず、高速で変化する圧力のみを通過させる。

インダクタは水車に相当する。水車の質量とブレードのサイズが大きいと、慣性によって水の流速はゆっくりとしか変化できなくなる。しかし、一定流速の流れは、充分な時間が経てば水車から抵抗を受けずに通過できるようになる。このとき水車は流速と等しい速度で回転している。水車の質量やブレード表面積はインダクタンスにあたり、軸とベアリングの間の摩擦はインダクタの抵抗に対応する。別のインダクタのモデルとして、単に長いパイプを考えることもできる。考えやすいように渦巻き状に捻ってあっても構わない。流体の慣性を利用するこのようなデバイスは、水槌ポンプの基幹部に実際に用いられている。パイプを通る流水の慣性はインダクタンスの効果をうみだす。インダクタは流れの急激な変化を「排除」して、遅い変化だけを通過させる。パイプ内壁から流体が受ける抵抗力は寄生抵抗に例えられる。いずれのモデルでも、最初に電流が流れ始める時にはインダクタをまたいだ圧力源（電圧）が必要である。このようにインダクタ中では電圧が電流を生み出す。電流が増加し、素子内部の摩擦や回路中の他の素子が定める限界の大きさに近づくにつれて、インダクタをまたいだ圧力低下は小さくなっていく。

理想的な電圧源（電池）はフィードバック制御付きのポンプである。両端に圧力計を置けば、電流がどんな値であってもこの種のポンプは一定の圧力差を作ることがわかる。回路の一端が接地されているなら、ポンプのモデルの代わりに、水が高い位置に貯められていて、多少の水が流れても水位が変化しないほど充分な量がある状況を考えてもよい。理想的な電流源のアナロジーを考えるためには容積式ポンプを用いることになる。流量計を付ければ、このようなポンプが一定速度で駆動すると流速が一定に保たれることがわかる。

• 
  シンプルなボール型チェックバルブ。開いた状態のバルブはダイオードのオン状態のように動作する。
• 
  圧力駆動バルブと一方通行のチェックバルブを組み合わせたものは（電界効果型）トランジスタとして動作する。
• 
  チェックバルブと同じく、ダイオードは望まない方向への流れをせき止める。正しい方向への流れはほとんど影響を受けない。
• 
  周期的な流れを作るポンプ、「ダイオード」バルブ、「コンデンサ」タンクからなる単純な交流回路。

ダイオードは一方通行のチェック弁に若干の漏れのあるバルブシートがついている状況と対応する。ダイオードと同様、バルブを開くには小さな圧力差が必要である。またダイオードと同じく、逆バイアスをかけすぎれば、バルブの損傷や破壊につながる。

トランジスタは小流量のシグナルによって制御されるバルブである。シグナルはバイポーラトランジスタでは一定の電流であり、FETでは一定の電圧である。シグナルに相当する流れはダイアフラムを通じてプランジャーを動かし、別のパイプのバルブを作動させて流れを制御する。

CMOSは2つのMOSFETを組み合わせたものである。入力圧力の変化により、ピストンが出力にゼロまたは正圧を接続する。

メモリスタは流量計によって制御されるニードルバルブである。順方向に水が流れると、針状のバルブが流れを絞るように動く。一方で逆向きに水が流れると、バルブが開いて抵抗を小さくする。

電磁波の速度（伝搬速度）は水中の音速に相当する。スイッチを入れたり閉じたりしたとき、電気的な波は導線中を素早く伝わる。

電荷の流れる速度（ドリフト速度）は水中の粒子の速度に相当する。粒子の速度は比較的ゆっくりとしか変化できない。

直流はパイプの回路においては一定流量の流れに相当する。

低周波の交流は水がパイプ中を前後に往復している状態に相当する。

高周波交流及び伝送線路は水のパイプを音波が伝播している状況に近い。ただし、このアナロジーは、交流電気回路で流れの向きが周期的に反転することを表してはいない。すでに述べたように、流体は圧力の変動は容易に伝える一方で、流量はゆっくりとしか変化させられないので、高周波では流れの反転は起こりえない。音波に例えられるのは、単純な交流電流ではなく直流電流に高周波のリップルが重ねられているような状況である。

誘導コイルでの誘導点火は水の慣性によるウォーターハンマーと類似している。

電気と流れが類似している例をいくつか挙げる。

type	水理学	電気	熱力学	力学
量	体積 ${\displaystyle V}$ [m3]	電荷 ${\displaystyle q}$ [C]	熱 ${\displaystyle Q}$ [J]	運動量 ${\displaystyle P}$ [N·s]
ポテンシャル	圧力 ${\displaystyle p}$ [Pa=J/m3=N/m2]	電位 ${\displaystyle \phi }$ [V=J/C=W/A]	温度 ${\displaystyle T}$ [K]	速度 ${\displaystyle v}$ [m/s]
流束	体積流量 ${\displaystyle \Phi _{V}}$ [m3/s]	電流 ${\displaystyle I}$ [A=C/s]	熱伝達率 ${\displaystyle {\dot {Q}}}$ [J/s]	力 ${\displaystyle F}$ [N]
流束密度	速度 ${\displaystyle v}$ [m/s]	電流密度 ${\displaystyle j}$ [C/(m2·s) = A/m²]	熱流束 ${\displaystyle {\dot {Q}}''}$ [W/m2]	応力 ${\displaystyle \sigma }$ [N/m2 = Pa]
線形モデル	ポアズイユの法則 ${\displaystyle \Phi _{V}={\frac {\pi r^{4}}{8\eta }}{\frac {\Delta p^{\star }}{\ell }}}$	オームの法則 ${\displaystyle j=-\sigma \nabla \phi }$	フーリエの法則 ${\displaystyle {\dot {Q}}''=\kappa \nabla T}$	ダッシュポット${\displaystyle \sigma =c\Delta v}$

微分方程式が同じ形であれば、応答は類似する。

この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方） 出典検索?: "水流モデル" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2018年4月)

水流モデルには限界もある。電気と水の振る舞いの異なる部分について認識することがこのアナロジーを有効に使う上で求められる。

場（マックスウェル方程式、インダクタンス）

電子は電磁場を介して遠くに離れた電子を押したり引いたりすることができる。一方で、水分子は直接接触した分子にのみ力を与えられる。このため、水中での波は音速で伝わるが、電荷の海を伝わる波の速度は音速よりずっと速くなる。また、水流ではエネルギーは水が波として伝えていくが、電気の場合には、電線のまわりの電磁場がエネルギーを伝えるのであって、導線中をエネルギーが伝わるわけではない。また、加速を受けている電子は、磁気力の作用により、周りの電子を引きずったり、引力を及ぼしたりする。

電荷

水とは異なり、荷電粒子は正負どちらの電荷も運ぶことができ、また導体は正味で正または負の電荷を持つことができる。電流に含まれている荷電粒子はほぼ電子であるが、状況によっては正電荷を持つ場合もある。実際、電解液中のH⁺ イオンやp型半導体の正孔などの例がある。

管の漏れ

電気回路、あるいは回路要素の中の電荷は通常ほぼゼロに等しく、したがって定数である。これはキルヒホッフの電流法則によって示されるが、液体の量は大抵一定ではなく、ここでは類似性はない。流体が非圧縮性であってさえ、回路にはピストンや開放端等が含まれることがあり、したがって系の特定の部分が持つ流体の体積は変化しうる。このため、電流を連続的に流す場合、開かれた湧き出し・吸い込み（水を出す蛇口と水を受けるバケツのようなもの）を持つ水力系で例えることはできず、閉ループにしなくてはならない。

流体速度と金属の抵抗

ホース中を流れる水と同様に、導体中の荷電粒子のドリフト速度は電流に直接比例する。しかし、パイプ中の水はパイプ内側表面でのみ抵抗を受けるが、電荷はむしろフィルターを通っている水と似ており、金属中のすべての点で抵抗を受ける。また、導体中での代表的な電荷の速度は毎分数センチメートルにさえ届かず、「電気摩擦」は非常に大きい。電荷がパイプ中の水並みの速度で動けば、電流は巨大になり、導体は加熱し、蒸発さえしてしまうだろう。金属中の抵抗と電荷速度をモデル化するには、スポンジを詰めたパイプ、または細いストローに満ちたシロップという方が、大口径のパイプよりはいいだろう。導体中の抵抗はほとんどの電気伝導体で定数である。つまり電流が増加すると、電圧降下がそれに比例して増加（オームの法則）する。液体のパイプ中での抵抗は流量に対して線形ではなく、2乗に比例する（ダルシー・ワイスバッハの式）。

量子力学

固体の導体や絶縁体に含まれる電荷は複数のエネルギー準位にわたっているが、パイプ中のある領域中の水が受ける圧力はただ1つの値を持つ。このため、電池による電荷の汲み上げ効果を水力系によって説明することはできない。ダイオードの空乏層および電圧降下、太陽電池、ペルチェ効果等についても同様に説明できない。しかし類似の応答を与える同等のデバイスを考えることはできる。

このモデルを的確に使うには、モデル系（水力系）の原理への相当な理解が求められる。また、水力系の原理の中でも電気回路に適用できるものだけを選ばなければいけない。水力系は一見シンプルである。しかしながら、あらゆる問題がそうなのではなく、たとえば、ポンプのキャビテーション は、よく知られた、複雑な問題で、流体や灌漑の専門家でもなければ、理解できない。「キャビテーション」に対応する電気工学の問題はない。電気回路の詳細な理論が必要となる局面では、水流モデルが誤った理解をもたらす可能性がある。

同様に、現実的に充分ありうるようなモデルを作り出すのは困難なこともある。上記の「電気の摩擦」は水流モデルではスポンジを詰めこんだパイプで表されたが、これが問題となる例で、どうしてもモデル化しようとすれば、現実的にはありそうもないほど複雑になってしまうのである。

ウィキメディア・コモンズには、水流モデルに関連するカテゴリがあります。

• 流体素子
• 水流回路（英語版） (油圧装置)
• 機械と電気の類似性（英語版）
• ボンドグラフ（英語版）
• 回路網熱力学