The title page of the original 1879 edition 『概念記法 』(がいねんきほう、独 : Begriffsschrift )は、ゴットロープ・フレーゲ によって1879年に出版された論理学 に関する短い本の題名であり、またその本で創始された形式体系 の名称である。
この本の完全な書名は「算術 の式言語 を模した、純粋な思考のための一つの式言語 eine der arithmetischen nachgebildete Formelsprache des reinen Denkens」である。『概念記法』は、アリストテレス が論理学という主題を創設して以来、論理学に関するおそらく最も重要な出版物であった。フレーゲ が自分の式を開発して論理に到達しようとした動機は、ライプニッツ が彼の推論計算機に対して持った動機と似ている。続いてフレーゲ は、数学の基礎の研究に彼の論理計算を用い、それは次の四半世紀にわたって遂行された。
Terrell Ward Bynumは『概念記法』の意義を11項目挙げている[ 1]
命題関数 の発明(第1章§9 関数)。「水素は二酸化炭素より軽い」を表す式言語において,「水素」の代わりに「酸素」あるいは「窒素」を代入することができる。そこで,「水素」を項,「二酸化炭素より軽い」を関数と呼ぶ。項Aの関数をΦ(A)のように書く。フレーゲは,それまで名辞(主語-述語)で表されていた命題を,関数で表したのである。
量化理論 の発明(§11 一般性)。「すべての(all)」や「ある(some)」を扱う量化記号を導入した。これによって「誰もが誰かを愛している」のような多重量化された文を扱うことができるようになった。
関係の祖先の最初の定式化(第3章§23- 系列の一般理論)。後述「祖先関係 」。
数学的帰納法の証明の最初の論理的分析(第3章§23- 系列の一般理論)。後述「祖先関係 」の「数学的帰納法 」。
(§10)。フレーゲは,Φ(A)において記号Φは他の記号Ψ,Xで置き換え可能なものであるから,Φ(A)を項Φの関数と見なすことができる,と言う。ここで彼は関数の関数を考えている。
この計算には,量化 された変数という概念が初めて導入され,また,高度に特異的な2次元表記法で表示されているとはいえ,同一性 を持った本質的に古典的な2値の二階論理である:結合子と限量子は,今日使用される¬,∧,∀ではなく,式をつなぐ線を用いて書かれる。たとえば,Bという判断に材料として判断Aが含まれること(実質含意),すなわち
B
→
A
{\displaystyle B\rightarrow A}
第1章でフレーゲ は,命題 (「判断」),全称量化子 (「一般性」),条件法,否定,内容の相等性のための記号
≡
{\displaystyle \equiv }
基本概念 フレーゲの表記法 現代的表記法
判断
⊢
A
,
⊩
A
{\displaystyle \vdash A,\Vdash A}
p(A)=1
否定
¬
A
;
∼
A
{\displaystyle \lnot A;\sim A}
条件法(含意)
B
→
A
{\displaystyle B\rightarrow A}
B
⊃
A
{\displaystyle B\supset A}
全称量化
∀
x
:
F
(
x
)
{\displaystyle \forall x:F(x)}
存在量化
∃
x
:
F
(
x
)
{\displaystyle \exists x:F(x)}
内容の相等性(等号) A≡B A=B
フレーゲ は条件法を次のように定義する。
「AとBが,判断可能な内容を意味するとき,次のような4つの可能性がある。
(1)
Aが肯定され,かつ,Bが肯定される,
(2)
Aが肯定され,かつ,Bが否定される,
(3)
Aが否定され,かつ,Bが肯定される,
(4)
Aが否定され,かつ,Bが否定される。
第2章でフレーゲ は,9つの式化された命題 を公理 として宣言し,それらは意図された意味を与えられて直観的真実を表現する,と非公式に論争してそれらを正当化した。現代的な表記法で再表現すると,これらの公理 は次のとおりである:
⊢
A
→
(
B
→
A
)
{\displaystyle \vdash \ \ A\rightarrow \left(B\rightarrow A\right)}
⊢
[
A
→
(
B
→
C
)
]
→
[
(
A
→
B
)
→
(
A
→
C
)
]
{\displaystyle \vdash \ \ \left[\ A\rightarrow \left(B\rightarrow C\right)\ \right]\ \rightarrow \ \left[\ \left(A\rightarrow B\right)\rightarrow \left(A\rightarrow C\right)\ \right]}
⊢
[
D
→
(
B
→
A
)
]
→
[
B
→
(
D
→
A
)
]
{\displaystyle \vdash \ \ \left[\ D\rightarrow \left(B\rightarrow A\right)\ \right]\ \rightarrow \ \left[\ B\rightarrow \left(D\rightarrow A\right)\ \right]}
⊢
(
B
→
A
)
→
(
¬
A
→
¬
B
)
{\displaystyle \vdash \ \ \left(B\rightarrow A\right)\ \rightarrow \ \left(\lnot A\rightarrow \lnot B\right)}
⊢
¬
¬
A
→
A
{\displaystyle \vdash \ \ \lnot \lnot A\rightarrow A}
⊢
A
→
¬
¬
A
{\displaystyle \vdash \ \ A\rightarrow \lnot \lnot A}
⊢
(
c
=
d
)
→
(
f
(
c
)
→
f
(
d
)
)
{\displaystyle \vdash \ \ \left(c=d\right)\rightarrow \left(f(c)\rightarrow f(d)\right)}
⊢
c
=
c
{\displaystyle \vdash \ \ c=c}
⊢
(
∀
a
:
f
(
a
)
)
→
f
(
c
)
{\displaystyle \vdash \ \ \left(\ \forall a:f(a)\ \right)\ \rightarrow \ f(c)}
これらは『概念記法 』の命題 1,2,8,28,31,41,52,54,および58である。 (1)-(3)は質量含意(実質含意)を支配する,(4)-(6)は否定,(7)および(8)は相等性,(9)は全称量化子である。 (7)はライプニッツ の不可識別者の同一性 を表現し,(8)は相等性が反射的であることを主張する。
他の命題 はすべて,(1)- (9)から次の推論規則を実施することによって推論される。
モドゥス・ポネンス は我々が
⊢
A
→
B
{\displaystyle \vdash A\to B}
⊢
A
{\displaystyle \vdash A}
⊢
B
{\displaystyle \vdash B}
全称汎化は,Pの中にxが現れなければ,我々が
⊢
P
→
A
(
x
)
{\displaystyle \vdash P\to A(x)}
⊢
P
→
∀
x
:
A
(
x
)
{\displaystyle \vdash P\rightarrow \forall x:A(x)}
フレーゲ が明示的に述べない代入の規則。 この規則は,はっきり正確に述べるのが前の2つの規則よりはるかに難しく,フレーゲ は明らかには正当でない方法でそれを実施する。
「系列の一般理論の若干のトピックス」という題名の第3章の主要な成果は,今日,祖先関係と呼ばれるものに関連している。フレーゲは,xに手続きfを適用した結果がyであることを,
⊢
f
(
x
,
y
)
{\displaystyle \vdash f(x,y)}
と表す(この記事では,現代記法で,xfy と書く)。また,フレーゲは,「xが性質Fを持ち,かつ,xに手続きfを適用した結果もつねに性質Fを持つ」とき,「性質Fはf系列において遺伝的である」(この記事では,Her(F)と書く[ 2]
∀
x
(
F
x
→
∀
y
(
x
f
y
→
F
y
)
)
≡
H
e
r
(
F
)
{\displaystyle \forall x(Fx\to \forall y(xfy\to Fy))\equiv Her(F)}
である。また,この記事では,「f系列でのxのすべての子ども(xに手続きfを適用した結果のすべて)が性質Fを持つ」ことをIn(x,F)と書く。すなわち,
∀
a
(
x
f
a
→
F
a
)
≡
I
n
(
x
,
F
)
{\displaystyle \forall a(xfa\to Fa)\equiv In(x,F)}
である。フレーゲは命題76で,xに手続きfを適用した結果のすべてが持つあらゆる遺伝的性質を,yが持つとき,「xはyの祖先である」あるいは「yはxの子孫である」(xf*yと書く)と定義した。
76:
⊩
∀
F
[
H
e
r
(
F
)
→
(
I
n
(
x
,
F
)
→
F
y
)
]
≡
x
f
∗
y
{\displaystyle \Vdash \forall F[Her(F)\to (In(x,F)\to Fy)]\equiv xf^{*}y}
命題81から,
⊢
F
x
→
[
H
e
r
(
F
)
→
x
f
∗
y
∨
y
=
x
→
F
y
)
]
{\displaystyle \vdash Fx\to [Her(F)\to xf^{*}y\vee y=x\to Fy)]}
が得られるが,これは数学的帰納法の原理を与えるものである。
命題98は,祖先関係が推移的であることを示す。
98:
⊢
x
f
∗
y
→
(
y
f
∗
z
→
x
f
∗
z
)
{\displaystyle \vdash xf^{*}y\to (yf^{*}z\to xf^{*}z)}
命題99は,「zは,xで始まるf系列に属する」(この記事では,xf*=z と書く)とは,「zは,xであるか,または,xの子孫である」ことと定義している。
99:
⊩
x
f
∗
z
∨
z
=
x
≡
x
f
∗
=
z
{\displaystyle \Vdash xf^{*}z\vee z=x\equiv xf^{*}=z}
命題115は,「fは関数的な(多対一の,一意的な)手続きである」(この記事ではFN(f)と書く)とは,yがxへの手続きfの適用結果であり,手続きfをxへ適用した結果がすべてyと同じであること,と定義している。
115:
⊩
∀
y
∀
x
[
x
f
y
→
∀
z
(
x
f
z
→
y
=
z
)
]
≡
F
N
(
f
)
{\displaystyle \Vdash \forall y\forall x[xfy\to \forall z(xfz\to y=z)]\equiv FN(f)}
最後の命題133は,手続きfが関数的で,mとyがf系列でxの子孫であるとき,yはmの祖先であるか,またはmで始まるf系列に属することを示す。
133:
⊢
F
N
(
f
)
→
[
x
f
∗
m
→
(
x
f
∗
y
→
y
f
∗
m
∨
m
f
∗
=
y
)
{\displaystyle \vdash FN(f)\to [xf^{*}m\to (xf^{*}y\to yf^{*}m\vee mf^{*}=y)}
フレーゲ は,祖先関係の成果を含む『概念記法 』の成果を,後の仕事『算術の基礎 』に適用した。
『概念記法 』がドイツの数学文献の中でどのように批評されたか,最近の注意深い研究として,リスト・ヴィルコ (1998年)を参照のこと。 何人かの批評家,特にエルンスト・シュレーダーは,全く好意的であった。『概念記法 』に続く形式論理の仕事はすべてこれに負っている,なぜなら2階論理は数学 と自然言語 のかなりの部分を表現する能力のある初めての形式論理だったからである。
フレーゲ の表記法の形跡のいくつかは,彼の「内容線」──と「判断線」│に起源を持つ「回転式木戸」記号
⊢
{\displaystyle \vdash }
フレーゲ は『概念記法 』で,ある命題 が(同語反復的に)真であると宣言するために,これらの記号を一体化した形|-で使用した。彼はある命題 が定義であるという印として「定義二重線」∥-を使用した。
なお,否定の印
¬
{\displaystyle \neg }
アレン・ハイティング [ 3]
ルートヴィヒ・ウィトゲンシュタイン の『論理哲学論考 』では,「概念記法 」の用語を論理的な形式主義の同義語として用いることによってフレーゲ に敬意を払っている。
フレーゲ の 1892年の小論『意義と意味 について』は,相等性(数学では=の記号で示される)についての『概念記法 』の結論のいくつかを撤回する。
人間の精神に対する言葉の支配を打ち破ることが哲学者の一つの任務であるならば,…私の概念記法 は,この目的のために更に開発されれば,哲学者にとって有用な道具になり得るであろう。…この概念記法 を発見したことだけでも,私には,論理学を推し進めたように思われる。(『概念記法 』への序文)
^ Bynum (1972) ^ Her(F),In(x,F),FN(f),*=などの記号は,田畑(2002)を参考にした。
^ Heyting, Arend (1930). “Die formalen Regeln der intuitionistischen Logik”. Sitzungsbericht PreuBische Akademie der Wissenschaften Berlin, physikalisch-mathematische Klasse II : 42–56.
Frege, Gottlob (1879). Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens . 略号[BS]. Halle. OCLC 560477756 翻訳:
二次文献:
ウィキメディア・コモンズには、
概念記法 に関連するカテゴリがあります。


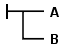



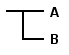




![{\displaystyle \vdash \ \ \left[\ A\rightarrow \left(B\rightarrow C\right)\ \right]\ \rightarrow \ \left[\ \left(A\rightarrow B\right)\rightarrow \left(A\rightarrow C\right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46233b0b84387b488948fe5ad59cef954c68fc83)
![{\displaystyle \vdash \ \ \left[\ D\rightarrow \left(B\rightarrow A\right)\ \right]\ \rightarrow \ \left[\ B\rightarrow \left(D\rightarrow A\right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdf8f5830ad951a8c528ea7eec78a90a79a61594)














![{\displaystyle \Vdash \forall F[Her(F)\to (In(x,F)\to Fy)]\equiv xf^{*}y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bd297c0d03ed4a774b96e82463ca0f5d54570d3)
![{\displaystyle \vdash Fx\to [Her(F)\to xf^{*}y\vee y=x\to Fy)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb47e0f49f723cf643c8ed70da1e973116d02823)


![{\displaystyle \Vdash \forall y\forall x[xfy\to \forall z(xfz\to y=z)]\equiv FN(f)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96a309e73d5fdf462324e9f65b016cbdae99e9f3)


