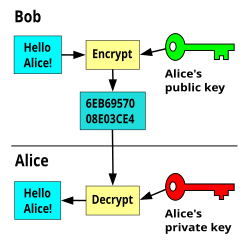
推測できない数(典型的にはランダム に生成した巨大な数)を用いて、最初に非対称鍵アルゴリズムに適した鍵 のペアを生成する。 非対称鍵暗号化のスキームでは、公開鍵を使用して誰でもメッセージを暗号化できるが、そのメッセージを復号できるのはペアの秘密鍵の所有者だけである。システムの安全性は、秘密鍵が秘匿されているという点に依存するので、秘密鍵は決して他の誰にも知られてはいけない。 この例では、メッセージは暗号化されたデジタル署名 である。まず、Aliceはメッセージを秘密鍵で署名する。次に、Bobは、Aliceがメッセージを送ったこと、そしてそのメッセージが変更されていないことを検証できる。 公開鍵暗号 (こうかいかぎあんごう、英語 : Public-key cryptography )とは、暗号化 と復号 とに異なる鍵 (手順)を用い、暗号化用の鍵は公開できるようにした暗号方式 である(復号用の鍵は秘匿)。対照的な暗号方式として、暗号化 と復号 に同一の鍵を用いる共通鍵暗号 がある。
暗号化 は通信の秘匿性 を高めるための手段だが、それに必須の鍵 もまた情報なので、鍵を受け渡す過程で盗聴されてしまうというリスクがあった。共通鍵を秘匿して受け渡すには(特使が運搬するというような)コストもかかり、一般人が暗号を用いる際の障害であった。このような暗号化鍵の配送問題を解決したのが公開鍵暗号である。
公開鍵暗号で使われるのと同じ数学的な理論に基づいて通信の安全性を保障する暗号技術全般を指して、広義に公開鍵暗号(あるいは公開鍵暗号技術、非対称暗号技術)と呼ぶこともある。この場合、通信の秘匿を目的とする公開鍵暗号方式だけでなく、秘匿機能は無いデジタル署名 、公開鍵通信路のみを用いて共通鍵を合意することができるディフィー・ヘルマン鍵交換 なども含まれる。
以下では、通信の秘匿を目的とした狭義での公開鍵暗号について扱う。
1976年以前には、数理による暗号といえば共通鍵暗号 であった。これは暗号化と復号に共通の鍵を使う方式である。共通鍵暗号には、鍵の受け渡しを密かに行わなければならないという課題(鍵配送問題)があった。
共通鍵暗号を用いた通信手順の概略は次のようになる。
あらかじめ、受信者と送信者は密かに共通鍵 c の受け渡しをしておく。
送信者は c を使ってメッセージを暗号化し、受信者に送信する。
受信者は c を使って暗号文を復号し、メッセージを読む。 もし段階 1. で、送信者に対してセキュリティが保証されていない通信路を用いて鍵を配送した場合、第三者に共通鍵 c を傍受されていると、この暗号通信は容易に解読されてしまう。
共通鍵暗号に生じる鍵配送問題は、送信者と受信者の両者がただ1つの共通の鍵を用いるために起こる問題である。そこで、両者が異なる鍵を用いる方法、すなわち公開鍵暗号 が考案された。
公開鍵暗号を用いた通信手順の概略:
通信を受ける者(受信者)は自分の公開鍵 (暗号化のための鍵)p を全世界に公開する。
受信者に対して暗号通信をする者(送信者)は、公開鍵 p を使ってメッセージを暗号化してから送信する。
受信者は、公開鍵 p と対になる秘密鍵(復号のための鍵)s を密かにもっている。この s を使って受信内容を復号し、送信者からのメッセージを読む。 暗号通信を不正に傍受しようとする者(傍受者)が公開鍵暗号の方式によって暗号化されたメッセージを傍受したとしても、公開鍵 p から秘密鍵 s を導き出すことは、計算時間の観点から 極めて難しいため、暗号文を復号することはおよそできない。
暗号化のための鍵と復号のための鍵を異なるものにしたことで、鍵配送問題は解決された。
なお、暗号の用語については、暗号理論の用語 、暗号の用語 を参照。
公開鍵暗号方式では、鍵生成アルゴリズム 、暗号化アルゴリズム 、復号アルゴリズム を用いる。
鍵生成アルゴリズムは事前準備のためのアルゴリズムであり、(将来暗号文を受け取りたい)ユーザは事前に鍵生成アルゴリズムを実行しておく必要がある。ユーザが鍵生成アルゴリズムを実行すると、アルゴリズムはそのユーザの公開鍵および秘密鍵(それぞれ、そのように呼ばれるデータ)を出力する。公開鍵は暗号文を作成するのに使い、秘密鍵はその暗号文からメッセージを復元するのに使う。
ユーザは鍵生成アルゴリズムを実行する際、セキュリティ・パラメータという値をこのアルゴリズムに入力する。セキュリティ・パラメータは、秘密鍵なしでの暗号文の解読がどれだけ困難かを示す尺度である。
鍵生成アルゴリズムには乱数も入力される。鍵生成アルゴリズムは実行ごとに異なる乱数を選ぶので、ユーザ毎に異なる公開鍵・秘密鍵ペアが割りふられる。
各ユーザは秘密鍵を密かに保管し、公開鍵を公開する。ユーザの秘密鍵を知っているのはそのユーザ自身だけであり、ユーザの公開鍵を知っている(知ることができる)のは全てのユーザである。
メッセージを秘匿する暗号通信をするときの公開鍵、秘密鍵を、それぞれ暗号化鍵 、復号鍵 ともいう。
暗号文を送る際は、送りたいメッセージおよびそのメッセージの送信先(受信者)の公開鍵を入力として暗号化アルゴリズムを実行する。
受信者は復号アルゴリズムに自分の秘密鍵と暗号文を入力して、もとのメッセージを復元する。
公開鍵を使えば誰でも 暗号文を作成できるが、その暗号文を正しく復号できるのは受信者本人だけである。
安全性を確保するには、どの公開鍵がどのユーザのものであるのかという対応をきちんとつけておく必要がある。暗号化に受信者の公開鍵 p を用いているので、もし、公開鍵 p とユーザとの対応が誤っていると、誤ったユーザの公開鍵を使って暗号文を送信してしまうことになる。これを悪用して、前もってあえて誤った対応表を作成しておくことによって暗号文を解くという攻撃が可能である(攻撃者は攻撃者自身の公開鍵をあたかも対象の受信者の公開鍵であるかのように見せた偽の対応表を作る。攻撃者の公開鍵を用いて暗号化された暗号文が対象の受信者へ送られたら、攻撃者はその暗号文を傍受して自身の秘密鍵で復号する。)。
公開鍵とその持ち主を対応させる方法はいくつか考案されている。代表的な方法は次の2つである。どちらも、信頼できる第三者機関 (英語版 )
信頼できる第三者機関が各人のIDと公開鍵を対応付けた表(公開鍵簿 )を作成して公開する。
信頼できる複数の第三者機関が認証 局を運営し、公開鍵基盤 (PKI) の仕組みを使って各人のIDと公開鍵とを対応付ける。
1960年代、イギリスの政府通信本部 (GCHQ) に所属するジェイムズ・エリス (英語版 ) 一方向性関数 が見つけられずこのアイデアは実用化されなかった。1973年、同機関に入所したクリフォード・コックス (英語版 ) マルコム・ウィリアムソン (英語版 ) RSA "と呼ばれる暗号システムの基礎を確立した。同時期に、彼らとは無関係な米国のアマチュア数学者、ウィットフィールド・デフィー が独学で公開鍵暗号開発に取り組んでいた。1976年 に、ラルフ・マークル の研究の影響を受けたデフィーとマーティン・ヘルマン が公開鍵暗号に関する世界最初の論文「New Directions in Cryptography[ 1] 」を発表した。
公開鍵暗号という新規な発明は、本来、エリス=コックス=ウィリアムソン組が先であったが、論文にして公表し、その有用性を広く伝えたのは、デフィー=ヘルマン=マークル組となったため、本発明の特許権と栄誉は彼らが得た。先に考案していたエリス=コックス=ウィリアムソン組は、英軍の管理下であったGCHQが国家機密となっていたために、後発組が公開鍵暗号の論文を発表しても、契約により口外できなかった。後年、公開鍵暗号が広く普及したことで本暗号に関する機密扱いが解除され、エリス=コックス=ウィリアムソン組の功績が世に知られることになった[ 2]
公開鍵暗号の概念を実現する具体的な方式は、MITの研究者であったロナルド・リベスト 、アディ・シャミア 、レオナルド・エーデルマン の3人が1977年 に開発した。この方式は、開発者各人の頭文字を取って「RSA方式」と呼ばれるようになった。1982年、彼らはカリフォリニア州レッドウッド市にデータセキュリティ専門の会社「RSAデータセキュリティ社」を設立した[ 3]
1990年代初頭、フィル・ジマーマン がパーソナル・コンピュータに搭載可能なプログラム「PGP(Pretty Good Privacy )」を開発し公開した。PGPが世界に普及したことで、誰でも公開鍵暗号が使用できるようになった。
公開鍵暗号は、1980年ごろには「公衆暗号 (public cryptography)」とも呼ばれていた。用語「公衆暗号系 (public cryptosystem)」も使われていたが、DES のような公衆が用いる共通鍵暗号を含むかどうかが紛らわしかったので、これらの用語はすぐに使われなくなった。
公開鍵暗号にはさまざまな方式がある。ここでは典型的な公開鍵暗号方式であるRSA暗号 方式を説明する。
この方式の安全性は素因数分解 の困難性に基づいている。詳しくはRSA暗号 を参照。
大きな素数 p, q が与えられたとき、その積 n = pq を計算することは容易である。しかし、2つの大きな素数の積である自然数 n が与えられたとき、それを n = pq と素因数分解することは難しい。例えば n=21 のときは n が小さいので p=7, q=3 を求めるのは容易だが、鍵の大きさ(すなわち p, q のビット 数)が十分に大きければ、素因数分解にはとてつもない時間が掛かる。
暗号化には n を、復号には p と q を必要とするようなうまい仕組みを作っておく。そして、n を公開鍵として公開する。傍受者は n から p, q を割り出そうとするが、これは時間が掛かりすぎて現実的でない。
根気強く素因数分解を試みていれば、いつかは復号できる。しかし、一般市民間の個人的な通信程度であれば、解読に数年を要する規模の暗号化を施しておけば、それ以上の手間を掛けて解読しようとする者はまずいない。これは、事実上秘密が守られているといえる(計算量的安全性 )。
一般的に、公開鍵暗号は共通鍵暗号よりも暗号化、復号に時間がかかる。そのため、実際の運用では、データの暗号化には「その場限りの共通鍵」を使用し、その共通鍵の配送だけを公開鍵暗号で行う方式がとられることが多い。
公開鍵暗号を初めて実現したのがRSA暗号である。RSA暗号は公開鍵暗号として、実際に広く利用されることとなった。
kをセキュリティ・パラメータとする。
Π
=
(
G
,
E
,
D
)
{\displaystyle \Pi =(G,E,D)}
多項式時間 確率アルゴリズム3つ組とする。
G
{\displaystyle G}
鍵生成アルゴリズム (key generation algorithm) と呼ばれ、
1
k
{\displaystyle 1^{k}}
(
p
k
,
s
k
)
{\displaystyle (\mathrm {pk} ,\mathrm {sk} )}
[ 注 1]
E
{\displaystyle E}
暗号化アルゴリズム (encryption algorithm) と呼ばれ、
G
{\displaystyle G}
p
k
{\displaystyle \mathrm {pk} }
平文 と呼ばれるビット列
m
{\displaystyle m}
m
{\displaystyle m}
暗号文 (Ciphertext) を出力する。
D
{\displaystyle D}
復号アルゴリズム (decryption algorithm) と呼ばれ、
G
{\displaystyle G}
s
k
{\displaystyle \mathrm {sk} }
E
{\displaystyle E}
C
{\displaystyle C}
Π
=
(
G
,
E
,
D
)
{\displaystyle \Pi =(G,E,D)}
Π
{\displaystyle \Pi }
公開鍵暗号方式 であるといい、後述する秘匿性をさらに満たすとき、公開鍵暗号方式は安全 であるという。
公開鍵暗号方式は、次の2つの要件を満たさねばならない。
正当性 (correctness) : 正当な受信者は、正当な方法で作成された暗号文を復号できる。
秘匿性 (security) : 正当な方法で作成された暗号文を復号できる(またはメッセージのなんらかの部分情報が得られる)のは、正当な受信者だけである。
定義
Π
=
(
G
,
E
,
D
)
{\displaystyle \Pi =(G,E,D)}
Π
{\displaystyle \Pi }
任意の平文 m に対し、Pr((pk, sk) ← G(1k ), C ← Epk (m) : Dsk (C) = m) は圧倒的 (overwhelming) である。
M
0
{\displaystyle M_{0}}
M
1
{\displaystyle M_{1}}
C
{\displaystyle C}
M
0
{\displaystyle M_{0}}
M
1
{\displaystyle M_{1}}
このとき、攻撃者は
C
{\displaystyle C}
M
0
{\displaystyle M_{0}}
M
1
{\displaystyle M_{1}}
O
1
{\displaystyle O_{1}}
O
2
{\displaystyle O_{2}}
b
{\displaystyle b}
暗号に対する攻撃者
A
{\displaystyle A}
実験 (Experiment, ゲーム (game) ともいう) をする。
E
x
p
Π
−
I
N
D
−
b
(
O
1
,
O
2
)
(
A
,
k
)
{\displaystyle {\mathsf {Exp}}_{\Pi -{\mathsf {IND}}-b}^{(O_{1},O_{2})}(A,k)}
(
p
k
,
s
k
)
←
G
(
1
k
)
{\displaystyle {\mathsf {(pk,sk)}}\gets G(1^{k})}
(
m
0
,
m
1
,
S
t
)
←
A
O
1
(
p
k
)
{\displaystyle (m_{0},m_{1},{\mathsf {St}})\gets A^{O_{1}}({\mathsf {pk}})}
C
←
E
p
k
(
m
b
)
{\displaystyle C\gets E_{\mathsf {pk}}(m_{b})}
b
′
←
A
O
2
(
p
k
,
C
,
S
t
)
{\displaystyle b'\gets A^{O_{2}}({\mathsf {pk}},C,{\mathsf {St}})}
Return
b
′
{\displaystyle b'}
攻撃者
A
{\displaystyle A}
アドバンテージ (advantage)を :
A
d
v
Π
−
I
N
D
(
O
1
,
O
2
)
(
A
,
k
)
=
|
P
r
(
E
x
p
Π
−
I
N
D
−
0
(
O
1
,
O
2
)
(
A
,
k
)
=
1
)
−
P
r
(
E
x
p
Π
−
I
N
D
−
1
(
O
1
,
O
2
)
(
A
,
k
)
=
1
)
|
{\displaystyle {\mathsf {Adv}}_{\Pi -{\mathsf {IND}}}^{(O_{1},O_{2})}(A,k)=|{\mathsf {Pr}}({\mathsf {Exp}}{}_{\Pi -{\mathsf {IND}}-0}^{(O_{1},O_{2})}(A,k)=1)-{\mathsf {Pr}}({\mathsf {Exp}}{}_{\Pi -{\mathsf {IND}}-1}^{(O_{1},O_{2})}(A,k)=1)|}
定義
任意の平均多項式時間確率アルゴリズム
A
{\displaystyle A}
攻撃者 と呼ぶ) に対し、
A
d
v
Π
(
O
1
,
O
2
)
(
A
,
k
)
{\displaystyle {\mathsf {Adv}}_{\Pi }^{(O_{1},O_{2})}(A,k)}
k に関して無視できるとき、暗号方式
Π
{\displaystyle \Pi }
(
O
1
,
O
2
)
{\displaystyle (O_{1},O_{2})}
識別不可能 (indistinguishable) であるという。
(注:この「
(
O
1
,
O
2
)
{\displaystyle (O_{1},O_{2})}
特に、
O
1
=
⊥
{\displaystyle O_{1}=\bot }
O
2
=
⊥
{\displaystyle O_{2}=\bot }
Π
{\displaystyle \Pi }
Key Only Attack に対し、識別不可能であるという。
O
1
=
O
d
e
c
(
s
k
,
∅
,
⋅
)
{\displaystyle O_{1}=O_{\mathsf {dec}}({\mathsf {sk}},\emptyset ,\cdot )}
O
2
=
⊥
{\displaystyle O_{2}=\bot }
Π
{\displaystyle \Pi }
選択暗号文攻撃 (Chosen Chiphertext Attack,(略してCCA1)) に対して識別不可能であるという。
O
1
=
O
d
e
c
(
s
k
,
∅
,
⋅
)
{\displaystyle O_{1}=O_{\mathsf {dec}}({\mathsf {sk}},\emptyset ,\cdot )}
O
2
=
O
d
e
c
(
s
k
,
{
m
0
,
m
1
}
,
⋅
)
{\displaystyle O_{2}=O_{\mathsf {dec}}({\mathsf {sk}},\{m_{0},m_{1}\},\cdot )}
Π
{\displaystyle \Pi }
適応的選択暗号文攻撃 (Adaptive Chosen Chiphertext Attack,(略してCCA2))に対して識別不可能であるという。 ただしここで
O
d
e
c
{\displaystyle O_{\mathsf {dec}}}
公開鍵暗号方式の場合暗号化用の鍵が公開されているので、攻撃者は(オラクルの助けを借りずとも)任意の平文を暗号化する事ができる。このため、Key Only Attackの事を選択平文攻撃 (Chosen Plaintest Attack, CPAと略す)ともいう。
復号オラクル
O
d
e
c
(
s
k
,
X
,
⋅
)
{\displaystyle O_{\mathsf {dec}}({\mathsf {sk}},X,\cdot )}
C
{\displaystyle C}
O
d
e
c
(
s
k
,
X
,
⋅
)
{\displaystyle O_{\mathsf {dec}}({\mathsf {sk}},X,\cdot )}
C
∉
X
{\displaystyle C\notin X}
s
k
{\displaystyle {\mathsf {sk}}}
C
{\displaystyle C}
D
s
k
(
C
)
{\displaystyle D_{\mathsf {sk}}(C)}
復号オラクル
O
d
e
c
(
s
k
,
X
,
C
)
{\displaystyle O_{\mathsf {dec}}({\mathsf {sk}},X,C)}
If
C
∈
X
{\displaystyle C\in X}
⊥
{\displaystyle \bot }
Otherwise return
D
s
k
(
C
)
{\displaystyle D_{\mathsf {sk}}(C)}
暗号文を知っていることは、平文を知る上で何の役にもたたない。すなわち、暗号文を知っている状況で攻撃者が知ることができる平文についての部分情報は、暗号文を知らなくても攻撃者が知ることができる情報だけである。
k
{\displaystyle k}
Π
=
(
G
,
E
,
D
)
{\displaystyle \Pi =(G,E,D)}
A
,
B
{\displaystyle A,B}
さらに、
O
1
,
O
2
{\displaystyle O_{1},O_{2}}
次の2つのゲームを考える。ただしゲーム中で、
M
,
f
{\displaystyle M,f}
S
t
{\displaystyle St}
A
{\displaystyle A}
状態 と呼ばれる。
E
x
p
Π
−
S
S
−
R
e
a
l
(
O
1
,
O
2
)
(
A
,
k
)
{\displaystyle {\mathsf {Exp}}_{\Pi -{\mathsf {SS-Real}}}^{(O_{1},O_{2})}(A,k)}
(
p
k
,
s
k
)
←
G
(
1
k
)
{\displaystyle {\mathsf {(pk,sk)}}\gets G(1^{k})}
(
M
,
S
t
)
←
A
O
1
(
p
k
)
{\displaystyle (M,{\mathsf {St}})\gets A^{O_{1}}({\mathsf {pk}})}
m
←
M
{\displaystyle m\gets M}
C
←
E
p
k
(
m
)
{\displaystyle C\gets E_{\mathsf {pk}}(m)}
(
y
,
f
)
←
A
O
2
(
C
,
S
t
)
{\displaystyle (y,f)\gets A^{O_{2}}(C,{\mathsf {St}})}
If
y
=
f
(
m
)
{\displaystyle y=f(m)}
Otherwise return 0.
E
x
p
Π
−
S
S
−
I
d
e
a
l
(
O
1
,
O
2
)
(
B
,
k
)
{\displaystyle {\mathsf {Exp}}_{\Pi -{\mathsf {SS-Ideal}}}^{(O_{1},O_{2})}(B,k)}
(
p
k
,
s
k
)
←
G
(
1
k
)
{\displaystyle {\mathsf {(pk,sk)}}\gets G(1^{k})}
(
M
,
S
t
)
←
B
O
1
(
p
k
)
{\displaystyle (M,{\mathsf {St}})\gets B^{O_{1}}({\mathsf {pk}})}
m
←
M
{\displaystyle m\gets M}
(
y
,
f
)
←
B
O
2
(
S
t
)
{\displaystyle (y,f)\gets B^{O_{2}}({\mathsf {St}})}
If
y
=
f
(
m
)
{\displaystyle y=f(m)}
Otherwise return 0. 任意の多項式時間機械
A
{\displaystyle A}
B
{\displaystyle B}
|
Pr
(
E
x
p
Π
−
S
S
−
R
e
a
l
(
O
1
,
O
2
)
(
A
,
k
)
=
1
)
−
Pr
(
E
x
p
Π
−
S
S
−
I
d
e
a
l
(
O
1
,
O
2
)
(
B
,
k
)
)
|
{\displaystyle |\Pr({\mathsf {Exp}}_{\Pi -{\mathsf {SS-Real}}}^{(O_{1},O_{2})}(A,k)=1)-\Pr({\mathsf {Exp}}_{\Pi -{\mathsf {SS-Ideal}}}^{(O_{1},O_{2})}(B,k))|}
が k に関して無視できるとき、公開鍵暗号方式
Π
=
(
G
,
E
,
D
)
{\displaystyle \Pi =(G,E,D)}
(
O
1
,
O
2
)
{\displaystyle (O_{1},O_{2})}
強秘匿 (Semantic Secure) であるという。
O
1
=
⊥
{\displaystyle O_{1}=\bot }
O
2
=
⊥
{\displaystyle O_{2}=\bot }
Π
{\displaystyle \Pi }
Key Only Attack に対し、強秘匿であるという。
O
1
=
O
d
e
c
(
s
k
,
∅
,
⋅
)
{\displaystyle O_{1}=O_{\mathsf {dec}}({\mathsf {sk}},\emptyset ,\cdot )}
O
2
=
⊥
{\displaystyle O_{2}=\bot }
Π
{\displaystyle \Pi }
選択暗号文攻撃 (Chosen Chiphertext Attack,(略してCCA1)) に対して強秘匿であるという。
O
1
=
O
d
e
c
(
s
k
,
∅
,
⋅
)
{\displaystyle O_{1}=O_{\mathsf {dec}}({\mathsf {sk}},\emptyset ,\cdot )}
O
2
=
O
d
e
c
(
s
k
,
{
m
0
,
m
1
}
,
⋅
)
{\displaystyle O_{2}=O_{\mathsf {dec}}({\mathsf {sk}},\{m_{0},m_{1}\},\cdot )}
Π
{\displaystyle \Pi }
適応的選択暗号文攻撃 (Adaptive Chosen Chiphertext Attack,(略してCCA2))に対して強秘匿であるという。
A
{\displaystyle A}
E
x
p
Π
−
N
M
−
b
(
O
1
,
O
2
)
(
A
,
k
)
{\displaystyle {\mathsf {Exp}}_{\Pi -{\mathsf {NM}}-b}^{(O_{1},O_{2})}(A,k)}
(
p
k
,
s
k
)
←
G
(
1
k
)
{\displaystyle {\mathsf {(pk,sk)}}\gets G(1^{k})}
(
M
,
S
t
)
←
A
O
1
(
p
k
)
{\displaystyle (M,{\mathsf {St}})\gets A^{O_{1}}({\mathsf {pk}})}
m
0
,
m
1
←
M
{\displaystyle m_{0},m_{1}\gets M}
C
←
E
p
k
(
m
b
)
{\displaystyle C\gets E_{\mathsf {pk}}(m_{b})}
(
R
,
C
1
′
,
…
,
C
n
′
)
←
A
O
2
(
C
,
S
t
)
{\displaystyle (R,C'_{1},\ldots ,C'_{n})\gets A^{O_{2}}(C,{\mathsf {St}})}
m
1
′
←
D
s
k
(
C
1
′
)
,
…
,
m
n
′
←
D
s
k
(
C
n
′
)
{\displaystyle m'_{1}\gets D_{\mathsf {sk}}(C'_{1}),\ldots ,m'_{n}\gets D_{\mathsf {sk}}(C'_{n})}
If
C
=
C
i
′
{\displaystyle C=C'_{i}}
i
{\displaystyle i}
If
m
i
′
=
⊥
{\displaystyle m'_{i}=\bot }
i
{\displaystyle i}
If
R
(
m
b
,
m
1
′
,
…
,
m
n
′
)
=
0
{\displaystyle R(m_{b},m'_{1},\ldots ,m'_{n})=0}
Return 1. ただし、上のゲームで、
M
{\displaystyle M}
任意の多項式時間機械
A
{\displaystyle A}
|
Pr
(
E
x
p
Π
−
N
M
−
1
(
O
1
,
O
2
)
(
A
,
k
)
=
1
)
−
Pr
(
E
x
p
Π
−
N
M
−
0
(
O
1
,
O
2
)
(
A
,
k
)
=
1
)
|
{\displaystyle |\Pr({\mathsf {Exp}}_{\Pi -{\mathsf {NM}}-1}^{(O_{1},O_{2})}(A,k)=1)-\Pr({\mathsf {Exp}}_{\Pi -{\mathsf {NM}}-0}^{(O_{1},O_{2})}(A,k)=1)|}
が k に関して無視できるとき、公開鍵暗号方式
Π
=
(
G
,
E
,
D
)
{\displaystyle \Pi =(G,E,D)}
(
O
1
,
O
2
)
{\displaystyle (O_{1},O_{2})}
non malleable であるという。
O
1
=
⊥
{\displaystyle O_{1}=\bot }
O
2
=
⊥
{\displaystyle O_{2}=\bot }
Π
{\displaystyle \Pi }
Key Only Attack に対し、頑強である (non malleable) という。
O
1
=
O
d
e
c
(
s
k
,
∅
,
⋅
)
{\displaystyle O_{1}=O_{\mathsf {dec}}({\mathsf {sk}},\emptyset ,\cdot )}
O
2
=
⊥
{\displaystyle O_{2}=\bot }
Π
{\displaystyle \Pi }
選択暗号文攻撃 (Chosen Chiphertext Attack,(略してCCA1))に対して頑強であるという。
O
1
=
O
d
e
c
(
s
k
,
∅
,
⋅
)
{\displaystyle O_{1}=O_{\mathsf {dec}}({\mathsf {sk}},\emptyset ,\cdot )}
O
2
=
O
d
e
c
(
s
k
,
{
m
0
,
m
1
}
,
⋅
)
{\displaystyle O_{2}=O_{\mathsf {dec}}({\mathsf {sk}},\{m_{0},m_{1}\},\cdot )}
Π
{\displaystyle \Pi }
適応的選択暗号文攻撃 (Adaptive Chosen Chiphertext Attack,(略してCCA2))に対して頑強であるという。
暗号関連
^ 入力の
1
k
{\displaystyle 1^{k}}
k
{\displaystyle k}
一進法 で表したものである。もし
k
{\displaystyle k}
l
o
g
2
k
{\displaystyle log_{2}k}
k
{\displaystyle k}
^ Whitfield Diffie; Martin Hellman (1976). “New directions in cryptography”. IEEE Transactions on Information Theory 22 (6): 644. doi :10.1109/TIT.1976.1055638 . ^ 井上孝司著、「通信と情報の保全 暗号化の話」『軍事研究2011年11月号』、(株)ジャパン・ミリタリー・レビュー、雑誌 03241-11、ISSN 0533-6716、227-228頁
^ Press Releases Archived 2011年9月29日, at the Wayback Machine . - RSA社サイト(英語、2012年2月19日閲覧)