|
Réseaux de régulation génique  Un réseau de régulation génique (ou génétique ) ( RRG ), réseau de régulation des gènes ou réseaux de régulation transcriptionnelle est un ensemble de régulateurs moléculaires qui interagissent entre eux et avec d'autres substances dans une cellule pour moduler l'expression génique de l'ARNm et des protéines qui, à leur tour, déterminent la fonction de la cellule. Les RRGs jouent un rôle central dans la morphogenèse, la création de structures corporelles, qui est un sujet phare de la biologie évolutive du développement. L'ADN, l'ARN, les protéines ou des assemblage de celles-ci peuvent agir comme des régulateurs de manière directe ou indirecte (via l'ARN transcrit ou la protéine traduite). En général, chaque molécule d'ARNm produit une protéine spécifique (ou un ensemble de protéines). Dans certains cas, cette protéine sera structurelle et s'accumulera au niveau de la membrane cellulaire ou à l'intérieur de la cellule pour lui conférer des propriétés structurelles particulières. Dans d'autres cas, la protéine sera une enzyme, c'est-à-dire une micro-machine qui catalyse une certaine réaction, telle que la dégradation d'une source alimentaire ou d'une toxine. Certaines protéines ne servent cependant qu'à activer d'autres gènes, et ce sont les facteurs de transcription qui sont les principaux acteurs des réseaux ou cascades de régulation. En se liant à la région promotrice au début d'autres gènes, ils les activent, initiant la production d'une autre protéine, et ainsi de suite. Certains facteurs de transcription sont inhibiteurs[1]. Dans les organismes unicellulaires, les réseaux de régulation répondent à l'environnement extérieur, optimisant la cellule à un instant donné pour sa survie dans cet environnement. Ainsi, une cellule de levure, se trouvant dans une solution sucrée, activera des gènes pour fabriquer des enzymes qui transforment le sucre en alcool[2]. Ce processus, que nous associons à la vinification, est la façon dont la cellule de levure gagne sa vie, gagnant de l'énergie pour se multiplier, ce qui, dans des circonstances normales, améliorerait ses perspectives de survie. Chez les animaux multicellulaires, le même principe a été mis au service des cascades de gènes qui contrôlent la forme du corps[3]. Chaque fois qu'une cellule se divise, il en résulte deux cellules qui, bien qu'elles contiennent le même génome dans son intégralité, peuvent différer quant aux gènes qui sont activés et fabriquent des protéines. Parfois, une «boucle de rétroaction auto-entretenue» garantit qu'une cellule conserve son identité et la transmet. Le mécanisme de l'épigénétique par lequel la modification de la chromatine peut fournir une mémoire cellulaire en bloquant ou en permettant la transcription est moins compris. Une caractéristique majeure des animaux multicellulaires est l'utilisation de gradients de morphogènes, qui fournissent en fait un système de positionnement qui indique à une cellule où elle se trouve dans le corps, et donc quel type de cellule devenir. Un gène qui est activé dans une cellule peut fabriquer un produit qui quitte la cellule et se diffuse à travers les cellules adjacentes, y pénétrant et n'activant les gènes que lorsqu'il est présent au-dessus d'un certain seuil. Ces cellules sont ainsi induites dans un nouveau destin et peuvent même générer d'autres morphogènes qui renvoient un signal à la cellule d'origine. Sur de plus longues distances, les morphogènes peuvent utiliser le processus actif de transduction du signal. Une telle signalisation contrôle l'embryogenèse, la construction d'un plan corporel à partir de zéro à travers une série d'étapes séquentielles. Ils contrôlent et entretiennent également les corps adultes par le biais de processus de rétroaction, et la perte de cette rétroaction en raison d'une mutation peut être responsable de la prolifération cellulaire observée dans le cancer. Parallèlement à ce processus de construction de la structure, la cascade de gènes active des gènes qui fabriquent des protéines structurelles qui confèrent à chaque cellule les propriétés physiques dont elle a besoin. AperçuÀ un certain niveau, les cellules biologiques peuvent être considérées comme des "sacs partiellement mélangés" de produits chimiques biologiques - dans la discussion sur les réseaux de régulation des gènes, ces produits chimiques sont principalement les ARN messagers (ARNm) et les protéines qui découlent de l'expression des gènes. Ces ARNm et protéines interagissent les uns avec les autres avec divers degrés de spécificité. Certains diffusent autour de la cellule. D'autres sont liés aux membranes cellulaires, interagissant avec les molécules de l'environnement. D'autres encore traversent les membranes cellulaires et véhiculent des signaux à longue portée vers d'autres cellules dans un organisme multicellulaire. Ces molécules et leurs interactions forment un réseau de régulation génique. 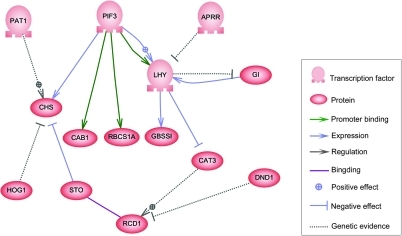 Les nœuds de ce réseau peuvent représenter des gènes, des protéines, des ARNm, des complexes protéine/protéine ou des processus cellulaires. Les nœuds représentés comme étant situés le long de lignes verticales sont associés aux interfaces cellule/environnement, tandis que les autres sont flottants et peuvent diffuser. Les bords entre les nœuds représentent des interactions entre les nœuds, qui peuvent correspondre à des réactions moléculaires individuelles entre l'ADN, l'ARNm, le miARN, les protéines ou les processus moléculaires par lesquels les produits d'un gène affectent ceux d'un autre, bien que le manque d'informations obtenues expérimentalement implique souvent que certains les réactions ne sont pas modélisées à un niveau de détail aussi fin. Ces interactions peuvent être inductives (généralement représentées par des pointes de flèches ou le signe +), avec une augmentation de la concentration de l'une entraînant une augmentation de l'autre, inhibitrices (représentées par des cercles pleins, des flèches mousses ou le signe moins), avec une augmentation dans l'un conduisant à une diminution de l'autre, ou double, lorsque selon les circonstances le régulateur peut activer ou inhiber le nœud cible. Les nœuds peuvent se réguler directement ou indirectement, créant des boucles de rétroaction, qui forment des chaînes cycliques de dépendances dans le réseau topologique. La structure du réseau est une abstraction de la dynamique moléculaire ou chimique du système, décrivant les multiples façons dont une substance affecte toutes les autres auxquelles elle est connectée. En pratique, de tels RRG sont déduits de la littérature biologique sur un système donné et représentent une distillation des connaissances collectives sur un ensemble de réactions biochimiques connexes. Pour accélérer la conservation manuelle des RRG, certains efforts récents tentent d'utiliser l'exploration de texte, les bases de données organisées, l'inférence de réseau à partir de données massives, la vérification de modèles et d'autres technologies d'extraction d'informations à cette fin[4]. Les gènes peuvent être considérés comme des nœuds dans le réseau, les entrées étant des protéines telles que les facteurs de transcription et les sorties étant le niveau d'expression des gènes. La valeur du nœud dépend d'une fonction qui dépend de la valeur de ses régulateurs dans les pas de temps précédents (dans le réseau booléen décrit ci-dessous, ce sont des fonctions booléennes, typiquement ET, OU et NON). Ces fonctions ont été interprétées comme effectuant une sorte de traitement de l'information au sein de la cellule, qui détermine le comportement cellulaire. Les moteurs de base dans les cellules sont les concentrations de certaines protéines, qui déterminent à la fois les coordonnées spatiales (emplacement dans la cellule ou le tissu) et temporelles (cycle cellulaire ou stade de développement) de la cellule, comme une sorte de "mémoire cellulaire". Les réseaux de gènes commencent seulement à être compris, et c'est une prochaine étape pour la biologie de tenter de déduire les fonctions de chaque "nœud" de gène, pour aider à comprendre le comportement du système dans des niveaux de complexité croissante, du gène à la voie de signalisation., au niveau cellulaire ou tissulaire[5]. Des modèles mathématiques de RRG ont été développés pour capturer le comportement du système modélisé et, dans certains cas, générer des prédictions correspondant aux observations expérimentales. Dans certains autres cas, les modèles se sont avérés faire de nouvelles prédictions précises, qui peuvent être testées expérimentalement, suggérant ainsi de nouvelles approches à explorer dans une expérience qui parfois ne seraient pas prises en compte dans la conception du protocole d'un laboratoire expérimental. Les techniques de modélisation comprennent les équations différentielles (ODE), les réseaux booléens, les réseaux de Petri, les réseaux bayésiens, les modèles graphiques de réseaux gaussiens, les stochastiques et les calculs de processus[6]. À l'inverse, des techniques ont été proposées pour générer des modèles de RRG qui expliquent au mieux un ensemble d'observations de séries chronologiques. Récemment, il a été montré que le signal ChIP-seq de la modification des histones est plus corrélé avec les motifs des facteurs de transcription au niveau des promoteurs par rapport au niveau de l'ARN[7]. Par conséquent, il est proposé que la modification des histones en série chronologique ChIP-seq pourrait fournir une inférence plus fiable des réseaux de régulation des gènes par rapport aux méthodes basées sur les niveaux d'expression. Structure et évolutionFonctionnalité globaleOn pense généralement que les réseaux de régulation des gènes sont constitués de quelques nœuds hautement connectés ( hubs ) et de nombreux nœuds mal connectés imbriqués dans un régime de régulation hiérarchique. Ainsi, les réseaux de régulation des gènes se rapprochent d'une topologie de réseau sans échelle hiérarchique[8]. Ceci est cohérent avec l'idée que la plupart des gènes ont une pléiotropie limitée et fonctionnent dans des modules de régulation[9]. On pense que cette structure évolue en raison de l' attachement préférentiel des gènes dupliqués à des gènes plus fortement connectés[8]. Des travaux récents ont également montré que la sélection naturelle tend à favoriser les réseaux à faible connectivité[10]. Les réseaux peuvent évoluer principalement de deux manières, les deux pouvant se produire simultanément. La première est que la topologie du réseau peut être modifiée par l'ajout ou la soustraction de nœuds (gènes) ou que des parties du réseau (modules) peuvent être exprimées dans différents contextes. La voie de signalisation de Drosophila Hippo en est un bon exemple. La voie de signalisation Hippo contrôle à la fois la croissance mitotique et la différenciation cellulaire post-mitotique[11]. Récemment, il a été découvert que le réseau dans lequel la voie de signalisation Hippo fonctionne diffère entre ces deux fonctions, ce qui modifie à son tour le comportement de la voie de signalisation Hippo. Cela suggère que la voie de signalisation Hippo fonctionne comme un module de régulation conservé qui peut être utilisé pour de multiples fonctions selon le contexte[11]. Ainsi, la modification de la topologie du réseau peut permettre à un module conservé de remplir plusieurs fonctions et de modifier la sortie finale du réseau. La deuxième façon dont les réseaux peuvent évoluer consiste à modifier la force des interactions entre les nœuds, comme la force avec laquelle un facteur de transcription peut se lier à un élément cis-régulateur. Il a été démontré qu'une telle variation de la force des bords du réseau sous-tend la variation entre les espèces dans le schéma du destin des cellules vulvaires des vers Caenorhabditis[12]. Caractéristique localeUne autre caractéristique largement citée du réseau de régulation des gènes est leur abondance de certains sous-réseaux répétitifs appelés motifs de réseau . Les motifs de réseau peuvent être considérés comme des motifs topologiques répétitifs lors de la division d'un grand réseau en petits blocs. Une analyse précédente a trouvé plusieurs types de motifs qui apparaissaient plus souvent dans les réseaux de régulation des gènes que dans les réseaux générés de manière aléatoire[13],[14],[15]. À titre d'exemple, un tel motif est appelé boucles de rétroaction, qui consistent en trois nœuds. Ce motif est le plus abondant parmi tous les motifs possibles constitués de trois nœuds, comme le montrent les réseaux de régulation des gènes de la mouche, du nématode et de l'homme[15]. Les motifs enrichis ont été proposés pour suivre une évolution convergente, suggérant qu'ils sont des "conceptions optimales" à certaines fins réglementaires[16]. Par exemple, la modélisation montre que les boucles d'anticipation sont capables de coordonner le changement du nœud A (en termes de concentration et d'activité) et la dynamique d'expression du nœud C, créant différents comportements d'entrée-sortie[17],[18]. Le système d'utilisation du galactose d' E. coli contient une boucle prédictive qui accélère l'activation de l'opéron d'utilisation du galactose galETK, facilitant potentiellement la transition métabolique vers le galactose lorsque le glucose est épuisé[19]. La boucle d'alimentation dans les systèmes d'utilisation de l'arabinose d'E. coli retarde l'activation de l'opéron et des transporteurs du catabolisme de l'arabinose, évitant potentiellement une transition métabolique inutile en raison de fluctuations temporaires dans les voies de signalisation en amont[20]. De même, dans la voie de signalisation Wnt de Xenopus, la boucle d'action directe agit comme un détecteur de changement de pli qui répond au changement de pli, plutôt qu'au changement absolu, du niveau de β-caténine, augmentant potentiellement la résistance aux fluctuations de β -niveaux de caténine[21]. Suivant l'hypothèse d'évolution convergente, l'enrichissement des boucles d'anticipation serait une adaptation pour une réponse rapide et une résistance au bruit. Une recherche récente a révélé que la levure cultivée dans un environnement de glucose constant développait des mutations dans les voies de signalisation du glucose et la voie de régulation de la croissance, suggérant que les composants régulateurs répondant aux changements environnementaux sont inutiles dans un environnement constant[22]. D'autre part, certains chercheurs émettent l'hypothèse que l'enrichissement des motifs de réseau est non adaptatif[23]. En d'autres termes, les réseaux de régulation des gènes peuvent évoluer vers une structure similaire sans sélection spécifique sur le comportement d'entrée-sortie proposé. Le soutien de cette hypothèse provient souvent de simulations informatiques. Par exemple, les fluctuations de l'abondance des boucles d'anticipation dans un modèle qui simule l'évolution des réseaux de régulation des gènes en recâblant de manière aléatoire des nœuds peuvent suggérer que l'enrichissement des boucles d'anticipation est un effet secondaire de l'évolution[24]. Dans un autre modèle d'évolution des réseaux de régulateurs de gènes, le rapport des fréquences de duplication et de suppression de gènes montre une grande influence sur la topologie du réseau : certains rapports conduisent à l'enrichissement des boucles d'alimentation et créent des réseaux qui présentent des caractéristiques de réseaux sans échelle hiérarchique. L'évolution de novo des boucles d'alimentation cohérentes de type 1 a été démontrée par calcul en réponse à la sélection de leur fonction hypothétique de filtrage d'un court signal parasite, prenant en charge l'évolution adaptative, mais pour le bruit non idéalisé, un système d'alimentation basé sur la dynamique. une régulation directe avec une topologie différente a été privilégiée[25]. Réseaux de régulation bactérienneLes réseaux de régulation permettent aux bactéries de s'adapter à presque toutes les niches environnementales de la planète[26],[27]. Un réseau d'interactions entre divers types de molécules, notamment l'ADN, l'ARN, les protéines et les métabolites, est utilisé par les bactéries pour réguler l'expression des gènes. Chez les bactéries, la fonction principale des réseaux de régulation est de contrôler la réponse aux changements environnementaux, par exemple l'état nutritionnel et le stress environnemental[28]. Une organisation complexe de réseaux permet au micro-organisme de coordonner et d'intégrer de multiples signaux environnementaux[26]. La modélisationÉquations différentielles ordinaires coupléesIl est courant de modéliser un tel réseau avec un ensemble d'équations différentielles ordinaires couplées (ODE) ou SDE, décrivant la cinétique de réaction des parties constituantes. Supposons que notre réseau réglementaire ait nœuds, et laissez représentent les concentrations de substances correspondantes au moment . Alors l'évolution temporelle du système peut être décrite approximativement par où les fonctions exprimer la dépendance de sur les concentrations d'autres substances présentes dans la cellule. Les fonctions sont finalement dérivés des principes de base de la cinétique chimique ou d'expressions simples dérivées de ceux-ci, par exemple Cinétique enzymatique de Michaelis-Menten. Ainsi, les formes fonctionnelles des sont généralement choisis comme polynômes d'ordre inférieur ou fonctions de Hill qui servent d'ansatz pour la dynamique moléculaire réelle. De tels modèles sont ensuite étudiés à l'aide des mathématiques de la dynamique non linéaire. Les informations spécifiques au système, telles que les constantes de vitesse de réaction et les sensibilités, sont codées sous forme de paramètres constants[29]. En résolvant pour le point fixe du système : pour tous , on obtient (éventuellement plusieurs) profils de concentration de protéines et d'ARNm qui sont théoriquement durables (mais pas nécessairement stables ). Les états stationnaires des équations cinétiques correspondent donc à des types cellulaires potentiels, et les solutions oscillatoires de l'équation ci-dessus à des types cellulaires naturellement cycliques. La stabilité mathématique de ces attracteurs peut généralement être caractérisée par le signe de dérivées supérieures aux points critiques, et correspond alors à la stabilité biochimique du profil de concentration. Les points critiques et les bifurcations dans les équations correspondent à des états cellulaires critiques dans lesquels de petites perturbations d'état ou de paramètre pourraient faire basculer le système entre l'un des plusieurs destins de différenciation stables. Les trajectoires correspondent au déroulement des voies biologiques et des transitoires des équations aux événements biologiques à court terme. Pour une discussion plus mathématique, voir les articles sur la non- linéarité, les systèmes dynamiques, la théorie de la bifurcation et la théorie du chaos. Réseau booléenL'exemple suivant illustre comment un réseau booléen peut modéliser un RRG avec ses produits géniques (les sorties) et les substances de l'environnement qui l'affectent (les entrées). Stuart Kauffman a été parmi les premiers biologistes à utiliser la métaphore des réseaux booléens pour modéliser les réseaux de régulation génétique[30],[31].
La validité du modèle peut être testée en comparant les résultats de simulation avec des observations de séries chronologiques. Une validation partielle d'un modèle de réseau booléen peut également provenir du test de l'existence prédite d'une connexion régulatrice encore inconnue entre deux facteurs de transcription particuliers qui sont chacun des nœuds du modèle[32]. Réseaux continusLes modèles de réseaux continus de RRG sont une extension des réseaux booléens décrits ci-dessus. Les nœuds représentent toujours les gènes et les connexions entre eux influencent la régulation de l'expression des gènes. Les gènes dans les systèmes biologiques affichent une gamme continue de niveaux d'activité et il a été avancé que l'utilisation d'une représentation continue capture plusieurs propriétés des réseaux de régulation des gènes non présentes dans le modèle booléen[33]. Formellement, la plupart de ces approches sont similaires à un réseau de neurones artificiels, car les entrées d'un nœud sont additionnées et le résultat sert d'entrée à une fonction sigmoïde, par exemple [34] mais les protéines contrôlent souvent l'expression des gènes de manière synergique, c'est-à-dire non. -linéaire, manière[35]. Cependant, il existe maintenant un modèle de réseau continu [36] qui permet le regroupement des entrées vers un nœud réalisant ainsi un autre niveau de régulation. Ce modèle est formellement plus proche d'un réseau neuronal récurrent d'ordre supérieur. Le même modèle a également été utilisé pour mimer l'évolution de la différenciation cellulaire [37] et même la morphogenèse multicellulaire[38]. Réseaux de gènes stochastiquesDes résultats expérimentaux récents [39],[40] ont démontré que l'expression des gènes est un processus stochastique. Ainsi, de nombreux auteurs utilisent maintenant le formalisme stochastique, après les travaux d'Arkin et al[41]. Les travaux sur l'expression d'un seul gène [42] et les petits réseaux génétiques synthétiques[43],[44], tels que l'interrupteur à bascule génétique de Tim Gardner et Jim Collins, ont fourni des données expérimentales supplémentaires sur la variabilité phénotypique et la nature stochastique de l'expression des gènes. Les premières versions des modèles stochastiques d'expression génique n'impliquaient que des réactions instantanées et étaient pilotées par l' algorithme de Gillespie[45]. Étant donné que certains processus, tels que la transcription génique, impliquent de nombreuses réactions et ne peuvent pas être correctement modélisés comme une réaction instantanée en une seule étape, il a été proposé de modéliser ces réactions en une seule étape plusieurs réactions retardées afin de tenir compte du temps qu'il faut pour l'ensemble du processus soit terminé[46]. À partir de là, un ensemble de réactions ont été proposées [47] qui permettent de générer des RRG. Ceux-ci sont ensuite simulés à l'aide d'une version modifiée de l'algorithme de Gillespie, qui peut simuler plusieurs réactions retardées (réactions chimiques où chacun des produits reçoit un délai qui détermine quand il sera libéré dans le système en tant que "produit fini") . Par exemple, la transcription de base d'un gène peut être représentée par la réaction en une seule étape suivante (RNAP est l'ARN polymérase, RBS est le site de liaison du ribosome à l'ARN et Pro i est la région promotrice du gène i ) : De plus, il semble y avoir un compromis entre le bruit dans l'expression des gènes, la vitesse à laquelle les gènes peuvent changer et le coût métabolique associé à leur fonctionnement. Plus précisément, pour un niveau donné de coût métabolique, il existe un compromis optimal entre le bruit et la vitesse de traitement et l'augmentation du coût métabolique conduit à de meilleurs compromis vitesse-bruit[48],[49],[50]. Un travail récent a proposé un simulateur (SGNSim, Stochastic Gene Networks Simulator )[51], qui peut modéliser les RRG où la transcription et la traduction sont modélisées comme de multiples événements retardés dans le temps et sa dynamique est pilotée par un algorithme de simulation stochastique (SSA) capable de traiter plusieurs événements retardés. Les temporisations peuvent être tirées de plusieurs distributions et les vitesses de réaction de fonctions complexes ou de paramètres physiques. SGNSim peut générer des ensembles de RRG dans un ensemble de paramètres définis par l'utilisateur, tels que la topologie. Il peut également être utilisé pour modéliser des RRG spécifiques et des systèmes de réactions chimiques. Les perturbations génétiques telles que les suppressions de gènes, la surexpression de gènes, les insertions, les mutations de décalage de cadre peuvent également être modélisées. Le RRG est créé à partir d'un graphe avec la topologie souhaitée, imposant des distributions en degré et hors degré. Les activités de promoteur de gènes sont affectées par d'autres produits d'expression de gènes qui agissent comme entrées, sous forme de monomères ou combinés en multimères et définis comme directs ou indirects. Ensuite, chaque entrée directe est affectée à un site opérateur et différents facteurs de transcription peuvent être autorisés ou non à concourir pour le même site opérateur, tandis que les entrées indirectes se voient attribuer une cible. Enfin, une fonction est attribuée à chaque gène, définissant la réponse du gène à une combinaison de facteurs de transcription (état promoteur). Les fonctions de transfert (c'est-à-dire la façon dont les gènes répondent à une combinaison d'entrées) peuvent être attribuées à chaque combinaison d'états de promoteur comme souhaité. Dans d'autres travaux récents, des modèles multi-échelles de réseaux de régulation des gènes ont été développés qui se concentrent sur les applications de la biologie synthétique. Des simulations ont été utilisées pour modéliser toutes les interactions biomoléculaires dans la transcription, la traduction, la régulation et l'induction des réseaux de régulation des gènes, guidant la conception de systèmes synthétiques[52]. PrédictionD'autres travaux se sont concentrés sur la prédiction des niveaux d'expression génique dans un réseau de régulation génique. Les approches utilisées pour modéliser les réseaux de régulation des gènes ont été contraintes d'être interprétables et, par conséquent, sont généralement des versions simplifiées du réseau. Par exemple, les réseaux booléens ont été utilisés en raison de leur simplicité et de leur capacité à gérer des données bruitées mais perdent des informations sur les données en ayant une représentation binaire des gènes. De plus, les réseaux de neurones artificiels omettent d'utiliser une couche cachée afin qu'ils puissent être interprétés, perdant la capacité de modéliser des corrélations d'ordre supérieur dans les données. En utilisant un modèle qui n'est pas contraint d'être interprétable, un modèle plus précis peut être produit. Être capable de prédire les expressions des gènes avec plus de précision fournit un moyen d'explorer comment les médicaments affectent un système de gènes et permet de connaître à l'avance les gènes interdépendants dans un processus. Cela a été encouragé par le concours DREAM [53]dont le but est de promouevoir de meilleurs algorithmes de prédiction[54]. Récemment, d'autres travaux ont utilisé des réseaux de neurones artificiels avec une couche cachée[55]. ApplicationsSclérose en plaquesLe réseau de régulation des gènes (RRG) joue un rôle essentiel pour comprendre les mécanismes de la maladie pour chacune des scléroses en plaques : récurrente-rémittente (RRMS), primaire progressive (PPMS) et secondaire progressive (SPMS)[56].
Références
Voir aussiDans wikipédiaLiens externes
|