|
Échantillonnage (statistiques)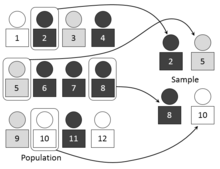 Pour les articles homonymes, voir Échantillonnage.  Cet article est une ébauche concernant les probabilités et la statistique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
 En statistique, l'échantillonnage — ou le sondage[réf. nécessaire] — désigne les méthodes de sélection d'un sous-ensemble d'individus (un échantillon) à l'intérieur d'une population pour estimer les caractéristiques de l'ensemble de la population. Cette méthode présente plusieurs avantages : une étude restreinte sur une partie de la population, un moindre coût, une collecte des données plus rapide que si l'étude avait été réalisé sur l'ensemble de la population, la réalisation de contrôles destructifs, etc. Les résultats obtenus constituent un échantillon. Sur un échantillon, on peut calculer différents paramètres statistiques de position (moyenne, etc.) ou de dispersion (écart type, etc.) issus de la statistique descriptive, de la même manière que l'on peut déterminer des paramètres statistiques d'une population par son recensement exhaustif. On peut également déduire des propriétés de la population à partir de celles de l'échantillon par inférence statistique. D'après la loi des grands nombres, plus la taille de l'échantillon augmente, plus ses propriétés seront proches de celle de la population. En particulier, on peut estimer une probabilité sur les individus d'une population par la fréquence observée sur un échantillon si sa taille est suffisamment grande. Par ailleurs, une moyenne ou une proportion dans une population peuvent être estimés par un intervalle de confiance. Cette démarche est employée dans le cadre des sondages d'opinions ou le contrôle statistique de la qualité. La « fluctuation d'échantillonnage » désigne la variabilité des résultats provenant de la prise d'échantillon. Plus la taille des échantillons est grande, moins il y a de fluctuation due à l'échantillonnage. La « distribution d'échantillonnage » d'un paramètre statistique regroupe toutes les valeurs possibles de ce paramètre sur l'ensemble de tous les échantillons d'une certaine taille qui pourraient être prélevés dans la population. On peut procéder de différentes manières pour collecter les données de l'échantillon, il existe en effet plusieurs méthodes d'échantillonnage. L'Échantillonnage aléatoire simple : le tirage des individus de l'échantillon est aléatoire, c'est-à-dire que chaque individu a la même probabilité d'être choisi, et simple, c'est-à-dire que les choix des différents individus sont réalisés indépendamment les uns des autres. L'Échantillonnage systématique : le premier individu est choisi de manière aléatoire, puis les suivants sont déterminés à intervalle régulier. Par exemple, dans un verger, on choisit au hasard le 7e pommier, puis les 27e, 47e, 67e, etc. L'Échantillonnage stratifié : on subdivise la population en plusieurs parties avant de prendre l'échantillon[1]. L'Échantillonnage par quotas : la composition de l'échantillon doit être représentative de celle de la population selon certains critères jugés particulièrement importants. On utilise cette méthode pour réaliser les sondages d'opinions[réf. nécessaire]. Jacques Dupâquier pour sa grande étude sur la démographie française utilise avec des ajustements le trigramme TRA, rassemblant la première lettre du patronyme des sujets de l'échantillon[2]. Cette méthode fut préconisée également pour l'échantillonnage des archives publiques jusqu'en 2014 où il est préconisé que seule la méthode systématique doit être retenue, le tri à partir de l'alphabet ou de la chronologie doit être abandonné[3]. Références
|
