|
Punto de Misiurewicz En matemáticas, un punto de Misiurewicz es un parámetro en el conjunto de Mandelbrot (el espacio de parámetros de los polinomios cuadráticos) para el que el punto crítico es estrictamente preperiódico (es decir, se vuelve periódico después de un número finito de iteraciones pero no es periódico en sí mismo). Por analogía, el término punto de Misiurewicz también se usa para parámetros en un conjunto multibrot en el que el punto crítico único es estrictamente preperiódico. Este término tiene menos sentido para aplicaciones de mayor generalidad que tienen más de un punto crítico (libre) porque algunos puntos críticos pueden ser periódicos y otros no. Notación matemáticaUn parámetro es un punto de Misiurewicz si satisface las ecuaciones y Entonces: donde:
DenominaciónLos puntos de Misiurewicz llevan el nombre del matemático polaco-estadounidense Michał Misiurewicz.[1] El término "punto de Misiurewicz" se usa de manera ambigua: Misiurewicz originalmente investigó aplicaciones en las que todos los puntos críticos eran no recurrentes (es decir, existe un entorno de cada punto crítico que no es visitado por la órbita de este punto crítico), significado que está firmemente establecido en el contexto de la dinámica de aplicaciones de intervalos iterados.[2] El caso de que para un polinomio cuadrático el punto crítico único sea estrictamente preperiódico es solo un caso muy especial. En este sentido restringido, el término se utiliza en dinámicas complejas; una denominación más apropiada sería puntos de Misiurewicz-Thurston (en referencia a William Thurston, que investigó las aplicaciones racionales poscríticamente finitas). Aplicaciones cuadráticasUn polinomio cuadrático complejo tiene solo un punto crítico. Mediante una conjugación adecuada, cualquier polinomio cuadrático se puede transformar en una aplicación de la forma que tiene un único punto crítico en . Los puntos de Misiurewicz de esta familia de aplicaciones son raíces de las ecuaciones
(sujeto a la condición de que el punto crítico no sea periódico), donde :
Por ejemplo, los puntos de Misiurewicz con k = 2 y n = 1, denotados por M2,1, son raíces de
La raíz c = 0 no es un punto de Misiurewicz porque el punto crítico es un punto fijo cuando c = 0, por lo que es periódico en lugar de preperiódico. Esto deja un único punto de Misiurewicz M2,1 en c = −2. Propiedades de los puntos de Misiurewicz de aplicaciones cuadráticas complejasLos puntos de Misiurewicz pertenecen a la frontera del conjunto de Mandelbrot. Los puntos de Misiurewicz son densos en el límite del conjunto de Mandelbrot.[3][4] Si es un punto de Misiurewicz, entonces el conjunto de Julia lleno asociado es igual al conjunto de Julia, y significa que el conjunto de Julia lleno no tiene interior. Si es un punto de Misiurewicz, entonces en el correspondiente conjunto de Julia todos los ciclos periódicos son repelentes (en particular, el ciclo en el que cae la órbita crítica). El conjunto de Mandelbrot y el conjunto de Julia son local y asintóticamente autosimilares alrededor de los puntos de Misiurewicz.[5] TiposLos puntos de Misiurewicz se pueden clasificar de acuerdo con la cantidad de rayos externos que inciden sobre ellos, es decir, los puntos donde se encuentran las ramas:[3]
Según el teorema de ramificación del conjunto de Mandelbrot,[4] todos los puntos de ramificación del conjunto de Mandelbrot son puntos de Misiurewicz. Además, en un sentido combinatorio, los componentes hiperbólicos están representados por sus centros.[3][4] La mayoría de los parámetros de Misiurewicz en el conjunto de Mandelbrot parecen "centros de espirales".[6] La explicación de este hecho es que en un parámetro de Misiurewicz, el valor crítico salta a un ciclo periódico repelente después de un número finito de iteraciones. En cada punto durante el ciclo, el conjunto de Julia es asintóticamente auto-similar por una multiplicación compleja por la derivada de este ciclo. Si la derivada no es real, esto implica que el conjunto de Julia cerca del ciclo periódico tiene una estructura en espiral. Por lo tanto, una estructura espiral similar se localiza en el conjunto de Julia cerca del valor crítico y, según el teorema de Tan Lei, también en el conjunto de Mandelbrot cerca de cualquier parámetro de Misiurewicz para el cual la órbita repelente tiene un multiplicador no real. Dependiendo del valor de este multiplicador, la forma de la espiral puede parecer más o menos pronunciada. El número de brazos en la espiral es igual al número de ramas en el parámetro Misiurewicz, y esto es igual al número de ramas en el valor crítico en el conjunto de Julia. Incluso el punto principal de Misiurewicz en la rama 1/3, al final de los rayos del parámetro en los ángulos 9/56, 11/56 y 15/56, resulta ser asintóticamente una espiral, con infinitas vueltas, aunque esto es difícil de ver sin aumento. Argumentos externosLos argumentos externos de los puntos de Misiurewicz, medidos en vueltas, son:
donde: a y b son números enteros positivos y b es impar, el número del subíndice muestra la base del sistema de numeración. Ejemplos de puntos de Misiurewicz de aplicaciones cuadráticas complejasPuntos finales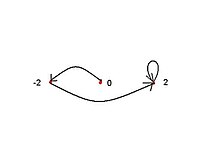  Punto :
Punto
Puntos de ramificación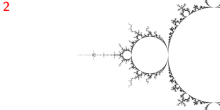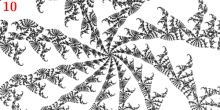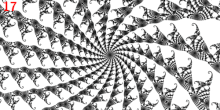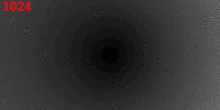  Punto :
Otros puntos Estos son puntos no son de ramificación ni finales. El punto está cerca de un punto de Misiurewicz. Es:
El punto está cerca de un punto de Misiurewicz,
Véase tambiénReferencias
Lecturas relacionadas
Enlaces externos
|












































