NP-hard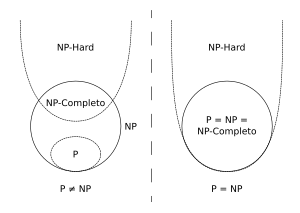

En teoría de la complejidad computacional, la clase de complejidad NP-hard (o NP-complejo, o NP-difícil) es el conjunto de los problemas de decisión que contiene los problemas H tales que todo problema L en NP puede ser transformado polinomialmente en H. Esta clase puede ser descrita como aquella que contiene a los problemas de decisión que son como mínimo tan difíciles como un problema de NP. Esta afirmación se justifica porque si podemos encontrar un algoritmo A que resuelve uno de los problemas H de NP-hard en tiempo polinómico, entonces es posible construir un algoritmo que trabaje en tiempo polinómico para cualquier problema de NP ejecutando primero la reducción de este problema en H y luego ejecutando el algoritmo A.

Asumiendo que el lenguaje L es NP-completo,

1. L está en NP

2. ∀L' en NP, L' ≤ L

En el conjunto NP-Hard se asume que el lenguaje L satisface la propiedad 2, pero no la propiedad 1.

La clase NP-completo puede definirse alternativamente como la intersección entre NP y NP-hard.

Algunas consecuencias de la definición son:

• Como NP-completo es el tipo más costoso de la clase NP, el problema H es al menos tan costoso como NP, pero H no tiene por qué estar en NP y por tanto no tiene por qué ser un problema de decisión.

• Los problemas NP-completos se pueden transformar unos en otros por una reducción polinómica, los problemas NP-completos pueden ser resueltos en tiempo polinómico por reducción a H, así que todos los problemas de NP se reducen a H; sin embargo, esto implica utilizar dos tipos diferentes de transformaciones: de problemas de decisión NP-completos a un problema NP-completo L por transformaciones polinómicas, y de L a H por reducción polinómica de Turing.

• Si hay algún algoritmo polinómico para resolver un problema NP-hard, entonces hay algoritmos para resolver todos los problemas de NP en tiempo polinómico, esto significaría que P=NP.

• Si un problema de optimización H tiene una versión NP-completa, entonces H es NP-hard.

• Si H pertenece a NP, entonces H pertenece también a NP-completo porque en este caso existe una transformación polinómica de Turing que cumple los requisitos de las transformaciones polinómicas.

Un error común es pensar que NP en NP-hard quiere decir no polinómico, ya que aunque hay serias sospechas sobre que no existen algoritmos para resolver estos problemas en tiempo polinómico, esto nunca ha sido demostrado.

El problema de la suma de subconjuntos es un ejemplo de problema NP-hard y se define como sigue: dado un conjunto S de enteros, ¿existe un subconjunto no vacío de S cuyos elementos sumen cero?

Existen problemas NP-hard que no son NP-completos, por ejemplo el problema de parada. Este problema consiste en tomar un programa y sus datos y decidir si va a terminar o si se ejecutará indefinidamente. Se trata de un problema de decisión y es fácil demostrar que es NP-hard pero no NP-completo. Por ejemplo, el problema de satisfacibilidad booleana puede reducirse al problema de parada transformándolo en la descripción de una máquina de Turing que prueba todos los valores de las variables; cuando encuentra una combinación que satisface la fórmula se detiene y en caso contrario reintenta desde el principio, quedándose en un lazo infinito. Para ver que el problema de parada no está en NP es suficiente notar que todos los problemas de NP tienen un algoritmo asociado pero el problema de la parada es indecidible.

Los nombres de familias de problemas con las siglas NP es algo confusa. Los problemas NP-hard no son todos NP, a pesar de que estas siglas aparecen es el nombre de la familia. Sin embargo, los nombres están actualmente muy arraigados y plantear un cambio de nomenclatura resulta poco realista. Por otra parte, las familias de problemas con las siglas NP son todas definidas tomando como referencia la familia NP:

NP-completo — significa problemas que son completos en NP, es decir, los más difíciles de resolver en NP;

NP-hard — (NP-difícil) quiere decir al menos tan complejo como NP (pero no necesariamente en NP);

NP-easy — (NP-fácil) quiere decir como mucho tan difícil como NP (pero no necesariamente en NP);

NP-equivalente — significa igualmente difícil que NP, (pero no necesariamente en NP).

• P (clase de complejidad)
• NP (clase de complejidad)
• NP-completo