Movimiento rectilíneo uniforme

En física, un movimiento es rectilíneo uniforme cuando un «objeto» (por ejemplo) viaja en una trayectoria recta a una velocidad constante,^[1]​ dado que su aceleración es nula.^[2]​

El movimiento rectilíneo uniforme se designa frecuentemente con el acrónimo MRU, aunque en algunos países se denomina como MRC, por movimiento rectilíneo constante.

El MRU se caracteriza por:

• Movimiento que se realiza sobre una línea recta.
• Velocidad constante; implica magnitud y dirección constantes.

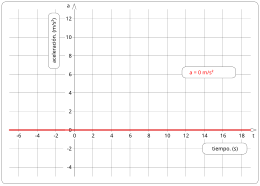
Para este tipo de movimiento, la distancia recorrida se calcula multiplicando la magnitud de la velocidad por el tiempo transcurrido. Esta relación también es aplicable si la trayectoria no es rectilínea, con tal que la rapidez o módulo de la velocidad sea constante. Por lo tanto, el movimiento puede considerarse en dos sentidos; una velocidad negativa representa un movimiento en dirección contraria al sentido que convencionalmente hayamos adoptado como positivo.

De acuerdo con la Primera Ley de Newton, toda partícula puntual permanece en reposo o en movimiento rectilíneo uniforme cuando no hay una fuerza externa que actúe sobre el cuerpo, dado que las fuerzas actuales están en equilibrio, por lo cual su estado es de reposo o de movimiento rectilíneo uniforme. Esta es una situación ideal, ya que siempre existen fuerzas que tienden a alterar el movimiento de las partículas, por lo que en el movimiento rectilíneo uniforme (MRU) es difícil encontrar la fuerza amplificada.

Una peculiaridad interesante de la trayectoria rectilínea, es que el problema admite una descripción unidimensional mediante una única coordenada, aunque estemos estudiando una trayectoria en tres dimensiones. Para ello basta escoger un punto sobre la trayectoria P y una función «distancia» al dicho punto d (será un número real, positivo para uno de los dos sentidos y negativo para el sentido opuesto), tomando el vector director unitario de la recta ${\displaystyle \mathbf {n} }$ existen dos elecciones posibles de este vector, cualquiera de las dos elecciones es esencialmente equivalente, el vector de posición ${\displaystyle \mathbf {r} }$ se podrá escribir siempre como:

${\displaystyle \mathbf {r} (t)=d(t)\mathbf {n} }$

La velocidad del punto material que ejecuta este movimiento se podrá escribir simplemente como

${\displaystyle \mathbf {v} (t)=v(t)\mathbf {n} =v(t)(n_{x}\mathbf {i} +n_{y}\mathbf {j} +n_{z}\mathbf {k} )}$

Si el movimiento es uniforme resultará que el vector posición es igual al vector velocidad por el tiempo:

${\displaystyle \mathbf {r} =\mathbf {v} \,t+\mathbf {r} _{0}}$

Descomponiendo el movimiento en cada uno de los ejes de coordenadas, la suma vectorial de estas componentes da como resultado la posición en el espacio del movimiento.

Si representamos la trayectoria rectilínea, en un sistema 2D, es una recta en el plano x-y, con un vector de posición: ${\displaystyle \mathbf {r} }$ , de coordenadas: ${\displaystyle r_{x},r_{y}}$.

${\displaystyle \mathbf {v} =v_{x}+v_{y}}$

El vector posición es igual al vector velocidad por el tiempo:

${\displaystyle \mathbf {r} =\mathbf {v} \,t}$

y conociendo las coordenadas de la velocidad tenemos.

${\displaystyle \mathbf {r} =v_{x}\,t+v_{y}\,t}$

Descomponiendo el movimiento en cada uno de los ejes de coordenadas, la suma vectorial de estas componentes da como resultado la posición en el plano del movimiento.

como forma de simplificación se suele tomar como eje de referencia uno paralelo al movimiento de forma que sea ese eje de referencia el único que intervenga, podemos ver esta representación si tomamos un movimiento vertical, sobre el eje x.

${\displaystyle x=v\,t}$

Del mismo modo, el movimiento se puede representar sobre el eje y, cuando el movimiento es vertical, tomando el valor positivo desde el origen de coordenadas hacia arriba, y desde el origen hacia abajo los valores negativos, en este caso los vectores solo tienen una coordenada y se pueden tomar perfectamente como escalares:

${\displaystyle y=v\,t}$

Como espacio es igual a la velocidad por el tiempo:

${\displaystyle e=v\,t}$

Al representar el desplazamiento en el eje y, y el tiempo en el eje x, siendo la aceleración, la velocidad y el desplazamiento función del tiempo, obteniendo gráfica de una función en un sistema de coordenadas cartesianas.

Sabemos que la velocidad ${\displaystyle \mathbf {v} }$ es constante; esto significa que no existe aceleración, la aceleración a es igual a cero.

${\displaystyle \mathbf {a} =0}$

La velocidad en función del tiempo se obtiene una recta paralela al al eje de abscisas (tiempo). Además, el área bajo la recta producida representa la distancia recorrida.

${\displaystyle \mathbf {v} =\mathbf {v_{0}} }$

La representación gráfica del espacio recorrido en función del tiempo da lugar a una recta cuya pendiente se corresponde con la velocidad.

${\displaystyle \mathbf {e} =\mathbf {e_{0}} +\mathbf {v} \,t}$

El Movimiento Rectilíneo Uniforme es una trayectoria recta, su velocidad es constante y su aceleración es nula.

La posición ${\displaystyle \mathbf {r} (t)}$ medido sobre el eje x, por ejemplo, en cualquier instante ${\displaystyle t\,}$ viene dada por:

${\displaystyle {\cfrac {de}{dt}}=v}$

${\displaystyle de=v\ dt}$

${\displaystyle \int _{e_{0}}^{e_{1}}de=v\int _{t_{0}}^{t_{1}}dt}$

${\displaystyle e_{1}-e_{0}=v(t_{1}-t_{0})}$

${\displaystyle e_{1}=e_{0}+v(t_{1}-t_{0})}$

Para una posición inicial ${\displaystyle \mathbf {e} _{0}}$ y un tiempo inicial ${\displaystyle t_{0}}$, ambos distintos de cero, la posición para cualquier tiempo está dada por

${\displaystyle e=e_{0}+vt}$

En astronomía, el MRU es muy utilizado. Los planetas y las estrellas no se mueven en línea recta, pero la que sí se mueve en línea recta es la luz, y siempre a la misma velocidad.

Entonces, sabiendo la distancia a la que se encuentra un objeto, se puede saber el tiempo que tarda la luz en recorrer esa distancia. Por ejemplo, el sol se encuentra a 150 000 000 km. La luz, por lo tanto, tarda 500 segundos (8 minutos 20 segundos) en llegar hasta la tierra. La realidad es un poco más compleja, con la relatividad de por medio, pero a grandes rasgos podemos decir que la luz sigue un movimiento rectilíneo uniforme.

• Física
• Cinemática
• Movimiento rectilíneo
• Movimiento rectilíneo uniformemente acelerado

• Antonio Máximo, Beatriz Alvarenga (2005). Física General. México D.F.: Oxford University Press. ISBN 970-613-147-7. 
• Beer, F. P., Johnston Jr, E. R., Mazurek, D. F., Cornwell, P. J., Eisenberg, E. R., & Sanghi, S. (1972). Vector mechanics for engineers (Vol. 1). Tata McGraw-Hill Education.

Ecuaciones de un MRU, E-Ducativa Catedu, Gobierno de Aragón. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).