|
Compuesto de diez tetraedros
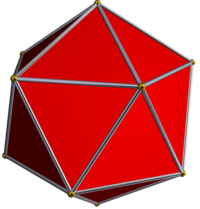
 El compuesto de diez tetraedros es uno de los cinco compuestos poliédricos regulares. Este poliedro puede verse como un estelación de icosaedro o como un compound. Este compuesto fue descrito por primera vez por Edmund Hess en 1876. Puede verse como un faceting de un dodecaedro regular. Como un compuesto También se puede ver como el compound de diez tetraedros con simetría icosaédrica (Ih). Es uno de los cinco compuestos regulares construidos a partir de Sólidos platónicos idénticos. Comparte el mismo disposición de vértices que un dodecaedro. El compuesto de cinco tetraedros representa dos mitades quirales de este compuesto (por lo tanto, puede verse como un "compuesto de dos compuestos de cinco tetraedros"). Se puede hacer a partir de compound of five cubes reemplazando cada cubo con un estrella octángula en los vértices del cubo (lo que da como resultado un "compuesto de cinco compuestos de dos tetraedros"). Como una estelaciónEste poliedro es una estelación del icosaedro, y como tal figura en el índice de modelos de Wenninger con el número 25.
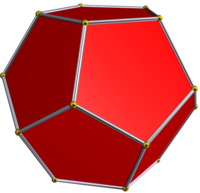
Como facetado También es un facetado del dodecaedro, como se muestra a la izquierda. Se pueden ver estrellas pentagonales cóncavas en el compuesto donde se colocan las caras pentagonales del dodecaedro. Como un poliedro simpleSi se trata como un poliedro no convexo simple sin superficies autointersecantes, tiene 180 caras (120 triángulos y 60 cuadriláteros cóncavos), 122 vértices (60 de grado 3, 30 de grado 4, 12 de grado 5 y 20 de grado 12), y 300 aristas, dando una característica de Euler de 122-300+180 = +2. Véase tambiénReferencias
Bibliografía
Enlaces externos
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||