|
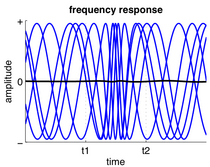
Neural oscillation  Neural oscillations, or brainwaves, are rhythmic or repetitive patterns of neural activity in the central nervous system. Neural tissue can generate oscillatory activity in many ways, driven either by mechanisms within individual neurons or by interactions between neurons. In individual neurons, oscillations can appear either as oscillations in membrane potential or as rhythmic patterns of action potentials, which then produce oscillatory activation of post-synaptic neurons. At the level of neural ensembles, synchronized activity of large numbers of neurons can give rise to macroscopic oscillations, which can be observed in an electroencephalogram. Oscillatory activity in groups of neurons generally arises from feedback connections between the neurons that result in the synchronization of their firing patterns. The interaction between neurons can give rise to oscillations at a different frequency than the firing frequency of individual neurons. A well-known example of macroscopic neural oscillations is alpha activity. Neural oscillations in humans were observed by researchers as early as 1924 (by Hans Berger). More than 50 years later, intrinsic oscillatory behavior was encountered in vertebrate neurons, but its functional role is still not fully understood.[3] The possible roles of neural oscillations include feature binding, information transfer mechanisms and the generation of rhythmic motor output. Over the last decades more insight has been gained, especially with advances in brain imaging. A major area of research in neuroscience involves determining how oscillations are generated and what their roles are. Oscillatory activity in the brain is widely observed at different levels of organization and is thought to play a key role in processing neural information. Numerous experimental studies support a functional role of neural oscillations; a unified interpretation, however, is still lacking. HistoryRichard Caton discovered electrical activity in the cerebral hemispheres of rabbits and monkeys and presented his findings in 1875.[4] Adolf Beck published in 1890 his observations of spontaneous electrical activity of the brain of rabbits and dogs that included rhythmic oscillations altered by light, detected with electrodes directly placed on the surface of the brain.[5] Before Hans Berger, Vladimir Vladimirovich Pravdich-Neminsky published the first animal EEG and the evoked potential of a dog.[6] OverviewNeural oscillations are observed throughout the central nervous system at all levels, and include spike trains, local field potentials and large-scale oscillations which can be measured by electroencephalography (EEG). In general, oscillations can be characterized by their frequency, amplitude and phase. These signal properties can be extracted from neural recordings using time-frequency analysis. In large-scale oscillations, amplitude changes are considered to result from changes in synchronization within a neural ensemble, also referred to as local synchronization. In addition to local synchronization, oscillatory activity of distant neural structures (single neurons or neural ensembles) can synchronize. Neural oscillations and synchronization have been linked to many cognitive functions such as information transfer, perception, motor control and memory.[7][8][9][10] The opposite of neuron synchronization is neural isolation, which is when electrical activity of neurons is not temporally synchronized. This is when the likelihood of the neuron to reach its threshold potential for the signal to propagate to the next neuron decreases. This phenomenon is typically observed as the spectral intensity decreases from the summation of these neurons firing, which can be utilized to differentiate cognitive function or neural isolation. However, new non-linear methods have been used that couple temporal and spectral entropic relationships simultaneously to characterize how neurons are isolated, (the signal's inability to propagate to adjacent neurons), an indicator of impairment (e.g., hypoxia).[1] Neural oscillations have been most widely studied in neural activity generated by large groups of neurons. Large-scale activity can be measured by techniques such as EEG. In general, EEG signals have a broad spectral content similar to pink noise, but also reveal oscillatory activity in specific frequency bands. The first discovered and best-known frequency band is alpha activity (8–12 Hz)[11][12][13] that can be detected from the occipital lobe during relaxed wakefulness and which increases when the eyes are closed.[14] Other frequency bands are: delta (1–4 Hz), theta (4–8 Hz), beta (13–30 Hz), low gamma (30–70 Hz),[15] and high gamma (70–150 Hz) frequency bands. Faster rhythms such as gamma activity have been linked to cognitive processing. Indeed, EEG signals change dramatically during sleep. In fact, different sleep stages are commonly characterized by their spectral content.[16] Consequently, neural oscillations have been linked to cognitive states, such as awareness and consciousness.[17][18][15][13] Although neural oscillations in human brain activity are mostly investigated using EEG recordings, they are also observed using more invasive recording techniques such as single-unit recordings. Neurons can generate rhythmic patterns of action potentials or spikes. Some types of neurons have the tendency to fire at particular frequencies, either as resonators[19] or as intrinsic oscillators.[2] Bursting is another form of rhythmic spiking. Spiking patterns are considered fundamental for information coding in the brain. Oscillatory activity can also be observed in the form of subthreshold membrane potential oscillations (i.e. in the absence of action potentials).[20] If numerous neurons spike in synchrony, they can give rise to oscillations in local field potentials. Quantitative models can estimate the strength of neural oscillations in recorded data.[21] Neural oscillations are commonly studied within a mathematical framework and belong to the field of "neurodynamics", an area of research in the cognitive sciences that places a strong focus on the dynamic character of neural activity in describing brain function.[22] It considers the brain a dynamical system and uses differential equations to describe how neural activity evolves over time. In particular, it aims to relate dynamic patterns of brain activity to cognitive functions such as perception and memory. In very abstract form, neural oscillations can be analyzed analytically.[23][24] When studied in a more physiologically realistic setting, oscillatory activity is generally studied using computer simulations of a computational model. The functions of neural oscillations are wide-ranging and vary for different types of oscillatory activity. Examples are the generation of rhythmic activity such as a heartbeat and the neural binding of sensory features in perception, such as the shape and color of an object. Neural oscillations also play an important role in many neurological disorders, such as excessive synchronization during seizure activity in epilepsy, or tremor in patients with Parkinson's disease. Oscillatory activity can also be used to control external devices such as a brain–computer interface.[25] PhysiologyOscillatory activity is observed throughout the central nervous system at all levels of organization. Three different levels have been widely recognized: the micro-scale (activity of a single neuron), the meso-scale (activity of a local group of neurons) and the macro-scale (activity of different brain regions).[26] 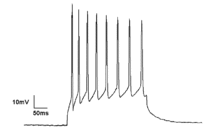 MicroscopicNeurons generate action potentials resulting from changes in the electric membrane potential. Neurons can generate multiple action potentials in sequence forming so-called spike trains. These spike trains are the basis for neural coding and information transfer in the brain. Spike trains can form all kinds of patterns, such as rhythmic spiking and bursting, and often display oscillatory activity.[27] Oscillatory activity in single neurons can also be observed in sub-threshold fluctuations in membrane potential. These rhythmic changes in membrane potential do not reach the critical threshold and therefore do not result in an action potential. They can result from postsynaptic potentials from synchronous inputs or from intrinsic properties of neurons. Neuronal spiking can be classified by its activity pattern. The excitability of neurons can be subdivided in Class I and II. Class I neurons can generate action potentials with arbitrarily low frequency depending on the input strength, whereas Class II neurons generate action potentials in a certain frequency band, which is relatively insensitive to changes in input strength.[19] Class II neurons are also more prone to display sub-threshold oscillations in membrane potential. MesoscopicA group of neurons can also generate oscillatory activity. Through synaptic interactions, the firing patterns of different neurons may become synchronized and the rhythmic changes in electric potential caused by their action potentials may accumulate (constructive interference). That is, synchronized firing patterns result in synchronized input into other cortical areas, which gives rise to large-amplitude oscillations of the local field potential. These large-scale oscillations can also be measured outside the scalp using electroencephalography (EEG) and magnetoencephalography (MEG). The electric potentials generated by single neurons are far too small to be picked up outside the scalp, and EEG or MEG activity always reflects the summation of the synchronous activity of thousands or millions of neurons that have similar spatial orientation.[28] Neurons in a neural ensemble rarely all fire at exactly the same moment, i.e. fully synchronized. Instead, the probability of firing is rhythmically modulated such that neurons are more likely to fire at the same time, which gives rise to oscillations in their mean activity. (See figure at top of page.) As such, the frequency of large-scale oscillations does not need to match the firing pattern of individual neurons. Isolated cortical neurons fire regularly under certain conditions, but in the intact brain, cortical cells are bombarded by highly fluctuating synaptic inputs and typically fire seemingly at random. However, if the probability of a large group of neurons firing is rhythmically modulated at a common frequency, they will generate oscillations in the mean field. (See also figure at top of page.)[27] Neural ensembles can generate oscillatory activity endogenously through local interactions between excitatory and inhibitory neurons. In particular, inhibitory interneurons play an important role in producing neural ensemble synchrony by generating a narrow window for effective excitation and rhythmically modulating the firing rate of excitatory neurons.[29] MacroscopicNeural oscillation can also arise from interactions between different brain areas coupled through the structural connectome. Time delays play an important role here. Because all brain areas are bidirectionally coupled, these connections between brain areas form feedback loops. Positive feedback loops tend to cause oscillatory activity where frequency is inversely related to the delay time. An example of such a feedback loop is the connections between the thalamus and cortex – the thalamocortical radiations. This thalamocortical network is able to generate oscillatory activity known as recurrent thalamo-cortical resonance.[30] The thalamocortical network plays an important role in the generation of alpha activity.[31][32] In a whole-brain network model with realistic anatomical connectivity and propagation delays between brain areas, oscillations in the beta frequency range emerge from the partial synchronisation of subsets of brain areas oscillating in the gamma-band (generated at the mesoscopic level).[33] MechanismsNeuronal propertiesScientists have identified some intrinsic neuronal properties that play an important role in generating membrane potential oscillations. In particular, voltage-gated ion channels are critical in the generation of action potentials. The dynamics of these ion channels have been captured in the well-established Hodgkin–Huxley model that describes how action potentials are initiated and propagated by means of a set of differential equations. Using bifurcation analysis, different oscillatory varieties of these neuronal models can be determined, allowing for the classification of types of neuronal responses. The oscillatory dynamics of neuronal spiking as identified in the Hodgkin–Huxley model closely agree with empirical findings. In addition to periodic spiking, subthreshold membrane potential oscillations, i.e. resonance behavior that does not result in action potentials, may also contribute to oscillatory activity by facilitating synchronous activity of neighboring neurons.[34][35] Like pacemaker neurons in central pattern generators, subtypes of cortical cells fire bursts of spikes (brief clusters of spikes) rhythmically at preferred frequencies.[2] Bursting neurons have the potential to serve as pacemakers for synchronous network oscillations, and bursts of spikes may underlie or enhance neuronal resonance.[27] Many of these neurons can be considered intrinsic oscillators, namely, neurons that generate their oscillations intrinsically, as their oscillation frequencies can be modified by local applications of glutamate in-vivo.[36] Network propertiesApart from intrinsic properties of neurons, biological neural network properties are also an important source of oscillatory activity. Neurons communicate with one another via synapses and affect the timing of spike trains in the post-synaptic neurons. Depending on the properties of the connection, such as the coupling strength, time delay and whether coupling is excitatory or inhibitory, the spike trains of the interacting neurons may become synchronized.[37] Neurons are locally connected, forming small clusters that are called neural ensembles. Certain network structures promote oscillatory activity at specific frequencies. For example, neuronal activity generated by two populations of interconnected inhibitory and excitatory cells can show spontaneous oscillations that are described by the Wilson-Cowan model. If a group of neurons engages in synchronized oscillatory activity, the neural ensemble can be mathematically represented as a single oscillator.[26] Different neural ensembles are coupled through long-range connections and form a network of weakly coupled oscillators at the next spatial scale. Weakly coupled oscillators can generate a range of dynamics including oscillatory activity.[38] Long-range connections between different brain structures, such as the thalamus and the cortex (see thalamocortical oscillation), involve time-delays due to the finite conduction velocity of axons. Because most connections are reciprocal, they form feed-back loops that support oscillatory activity. Oscillations recorded from multiple cortical areas can become synchronized to form large-scale brain networks, whose dynamics and functional connectivity can be studied by means of spectral analysis and Granger causality measures.[39] Coherent activity of large-scale brain activity may form dynamic links between brain areas required for the integration of distributed information.[18] Microglia – the major immune cells of the brain – have been shown to play an important role in shaping network connectivity, and thus, influencing neuronal network oscillations both ex vivo and in vivo. [40] NeuromodulationIn addition to fast direct synaptic interactions between neurons forming a network, oscillatory activity is regulated by neuromodulators on a much slower time scale. That is, the concentration levels of certain neurotransmitters are known to regulate the amount of oscillatory activity. For instance, GABA concentration has been shown to be positively correlated with frequency of oscillations in induced stimuli.[41] A number of nuclei in the brainstem have diffuse projections throughout the brain influencing concentration levels of neurotransmitters such as norepinephrine, acetylcholine and serotonin. These neurotransmitter systems affect the physiological state, e.g., wakefulness or arousal, and have a pronounced effect on amplitude of different brain waves, such as alpha activity.[42] Mathematical descriptionOscillations can often be described and analyzed using mathematics. Mathematicians have identified several dynamical mechanisms that generate rhythmicity. Among the most important are harmonic (linear) oscillators, limit cycle oscillators, and delayed-feedback oscillators.[43] Harmonic oscillations appear very frequently in nature—examples are sound waves, the motion of a pendulum, and vibrations of every sort. They generally arise when a physical system is perturbed by a small degree from a minimum-energy state, and are well understood mathematically. Noise-driven harmonic oscillators realistically simulate alpha rhythm in the waking EEG as well as slow waves and spindles in the sleep EEG. Successful EEG analysis algorithms were based on such models. Several other EEG components are better described by limit-cycle or delayed-feedback oscillations. Limit-cycle oscillations arise from physical systems that show large deviations from equilibrium, whereas delayed-feedback oscillations arise when components of a system affect each other after significant time delays. Limit-cycle oscillations can be complex but there are powerful mathematical tools for analyzing them; the mathematics of delayed-feedback oscillations is primitive in comparison. Linear oscillators and limit-cycle oscillators qualitatively differ in terms of how they respond to fluctuations in input. In a linear oscillator, the frequency is more or less constant but the amplitude can vary greatly. In a limit-cycle oscillator, the amplitude tends to be more or less constant but the frequency can vary greatly. A heartbeat is an example of a limit-cycle oscillation in that the frequency of beats varies widely, while each individual beat continues to pump about the same amount of blood. Computational models adopt a variety of abstractions in order to describe complex oscillatory dynamics observed in brain activity. Many models are used in the field, each defined at a different level of abstraction and trying to model different aspects of neural systems. They range from models of the short-term behaviour of individual neurons, through models of how the dynamics of neural circuitry arise from interactions between individual neurons, to models of how behaviour can arise from abstract neural modules that represent complete subsystems. Single neuron model A model of a biological neuron is a mathematical description of the properties of nerve cells, or neurons, that is designed to accurately describe and predict its biological processes. One of the most successful neuron models is the Hodgkin–Huxley model, for which Hodgkin and Huxley won the 1963 Nobel Prize in physiology or medicine. The model is based on data from the squid giant axon and consists of nonlinear differential equations that approximate the electrical characteristics of a neuron, including the generation and propagation of action potentials. The model is so successful at describing these characteristics that variations of its "conductance-based" formulation continue to be utilized in neuron models over a half a century later.[44] The Hodgkin–Huxley model is too complicated to understand using classical mathematical techniques, so researchers often turn to simplifications such as the FitzHugh–Nagumo model and the Hindmarsh–Rose model, or highly idealized neuron models such as the leaky integrate-and-fire neuron, originally developed by Lapique in 1907.[45][46] Such models only capture salient membrane dynamics such as spiking or bursting at the cost of biophysical detail, but are more computationally efficient, enabling simulations of larger biological neural networks. Spiking modelA neural network model describes a population of physically interconnected neurons or a group of disparate neurons whose inputs or signalling targets define a recognizable circuit. These models aim to describe how the dynamics of neural circuitry arise from interactions between individual neurons. Local interactions between neurons can result in the synchronization of spiking activity and form the basis of oscillatory activity. In particular, models of interacting pyramidal cells and inhibitory interneurons have been shown to generate brain rhythms such as gamma activity.[47] Similarly, it was shown that simulations of neural networks with a phenomenological model for neuronal response failures can predict spontaneous broadband neural oscillations.[48] Neural mass model Neural field models are another important tool in studying neural oscillations and are a mathematical framework describing evolution of variables such as mean firing rate in space and time. In modeling the activity of large numbers of neurons, the central idea is to take the density of neurons to the continuum limit, resulting in spatially continuous neural networks. Instead of modelling individual neurons, this approach approximates a group of neurons by its average properties and interactions. It is based on the mean field approach, an area of statistical physics that deals with large-scale systems. Models based on these principles have been used to provide mathematical descriptions of neural oscillations and EEG rhythms. They have for instance been used to investigate visual hallucinations.[50] Kuramoto modelThe Kuramoto model of coupled phase oscillators[51] is one of the most abstract and fundamental models used to investigate neural oscillations and synchronization. It captures the activity of a local system (e.g., a single neuron or neural ensemble) by its circular phase alone and hence ignores the amplitude of oscillations (amplitude is constant).[52] Interactions amongst these oscillators are introduced by a simple algebraic form (such as a sine function) and collectively generate a dynamical pattern at the global scale. The Kuramoto model is widely used to study oscillatory brain activity, and several extensions have been proposed that increase its neurobiological plausibility, for instance by incorporating topological properties of local cortical connectivity.[53] In particular, it describes how the activity of a group of interacting neurons can become synchronized and generate large-scale oscillations. Simulations using the Kuramoto model with realistic long-range cortical connectivity and time-delayed interactions reveal the emergence of slow patterned fluctuations that reproduce resting-state BOLD functional maps, which can be measured using fMRI.[54] Activity patternsBoth single neurons and groups of neurons can generate oscillatory activity spontaneously. In addition, they may show oscillatory responses to perceptual input or motor output. Some types of neurons will fire rhythmically in the absence of any synaptic input. Likewise, brain-wide activity reveals oscillatory activity while subjects do not engage in any activity, so-called resting-state activity. These ongoing rhythms can change in different ways in response to perceptual input or motor output. Oscillatory activity may respond by increases or decreases in frequency and amplitude or show a temporary interruption, which is referred to as phase resetting. In addition, external activity may not interact with ongoing activity at all, resulting in an additive response. Oscillatory responses Ongoing activitySpontaneous activity is brain activity in the absence of an explicit task, such as sensory input or motor output, and hence also referred to as resting-state activity. It is opposed to induced activity, i.e. brain activity that is induced by sensory stimuli or motor responses. The term ongoing brain activity is used in electroencephalography and magnetoencephalography for those signal components that are not associated with the processing of a stimulus or the occurrence of specific other events, such as moving a body part, i.e. events that do not form evoked potentials/evoked fields, or induced activity. Spontaneous activity is usually considered to be noise if one is interested in stimulus processing; however, spontaneous activity is considered to play a crucial role during brain development, such as in network formation and synaptogenesis. Spontaneous activity may be informative regarding the current mental state of the person (e.g. wakefulness, alertness) and is often used in sleep research. Certain types of oscillatory activity, such as alpha waves, are part of spontaneous activity. Statistical analysis of power fluctuations of alpha activity reveals a bimodal distribution, i.e. a high- and low-amplitude mode, and hence shows that resting-state activity does not just reflect a noise process.[55] In case of fMRI, spontaneous fluctuations in the blood-oxygen-level dependent (BOLD) signal reveal correlation patterns that are linked to resting state networks, such as the default network.[56] The temporal evolution of resting state networks is correlated with fluctuations of oscillatory EEG activity in different frequency bands.[57] Ongoing brain activity may also have an important role in perception, as it may interact with activity related to incoming stimuli. Indeed, EEG studies suggest that visual perception is dependent on both the phase and amplitude of cortical oscillations. For instance, the amplitude and phase of alpha activity at the moment of visual stimulation predicts whether a weak stimulus will be perceived by the subject.[58][59][60] Frequency responseIn response to input, a neuron or neuronal ensemble may change the frequency at which it oscillates, thus changing the rate at which it spikes. Often, a neuron's firing rate depends on the summed activity it receives. Frequency changes are also commonly observed in central pattern generators and directly relate to the speed of motor activities, such as step frequency in walking. However, changes in relative oscillation frequency between different brain areas is not so common because the frequency of oscillatory activity is often related to the time delays between brain areas. Amplitude responseNext to evoked activity, neural activity related to stimulus processing may result in induced activity. Induced activity refers to modulation in ongoing brain activity induced by processing of stimuli or movement preparation. Hence, they reflect an indirect response in contrast to evoked responses. A well-studied type of induced activity is amplitude change in oscillatory activity. For instance, gamma activity often increases during increased mental activity such as during object representation.[61] Because induced responses may have different phases across measurements and therefore would cancel out during averaging, they can only be obtained using time-frequency analysis. Induced activity generally reflects the activity of numerous neurons: amplitude changes in oscillatory activity are thought to arise from the synchronization of neural activity, for instance by synchronization of spike timing or membrane potential fluctuations of individual neurons. Increases in oscillatory activity are therefore often referred to as event-related synchronization, while decreases are referred to as event-related desynchronization.[62] Phase resettingPhase resetting occurs when input to a neuron or neuronal ensemble resets the phase of ongoing oscillations.[63] It is very common in single neurons where spike timing is adjusted to neuronal input (a neuron may spike at a fixed delay in response to periodic input, which is referred to as phase locking[19]) and may also occur in neuronal ensembles when the phases of their neurons are adjusted simultaneously. Phase resetting is fundamental for the synchronization of different neurons or different brain regions[18][38] because the timing of spikes can become phase locked to the activity of other neurons. Phase resetting also permits the study of evoked activity, a term used in electroencephalography and magnetoencephalography for responses in brain activity that are directly related to stimulus-related activity. Evoked potentials and event-related potentials are obtained from an electroencephalogram by stimulus-locked averaging, i.e. averaging different trials at fixed latencies around the presentation of a stimulus. As a consequence, those signal components that are the same in each single measurement are conserved and all others, i.e. ongoing or spontaneous activity, are averaged out. That is, event-related potentials only reflect oscillations in brain activity that are phase-locked to the stimulus or event. Evoked activity is often considered to be independent from ongoing brain activity, although this is an ongoing debate.[64][65] Asymmetric amplitude modulationIt has recently been proposed that even if phases are not aligned across trials, induced activity may still cause event-related potentials because ongoing brain oscillations may not be symmetric and thus amplitude modulations may result in a baseline shift that does not average out.[66][67] This model implies that slow event-related responses, such as asymmetric alpha activity, could result from asymmetric brain oscillation amplitude modulations, such as an asymmetry of the intracellular currents that propagate forward and backward down the dendrites.[68] Under this assumption, asymmetries in the dendritic current would cause asymmetries in oscillatory activity measured by EEG and MEG, since dendritic currents in pyramidal cells are generally thought to generate EEG and MEG signals that can be measured at the scalp.[69] Cross-frequency couplingCross-frequency coupling (CFC) describes the coupling (statistical correlation) between a slow wave and a fast wave. There are many kinds, generally written as A-B coupling, meaning the A of a slow wave is coupled with the B of a fast wave. For example, phase–amplitude coupling is where the phase of a slow wave is coupled with the amplitude of a fast wave.[70] The theta-gamma code is a coupling between theta wave and gamma wave in the hippocampal network. During a theta wave, 4 to 8 non-overlapping neuron ensembles are activated in sequence. This has been hypothesized to form a neural code representing multiple items in a temporal frame [71][72] FunctionNeural synchronization can be modulated by task constraints, such as attention, and is thought to play a role in feature binding,[73] neuronal communication,[7] and motor coordination.[9] Neuronal oscillations became a hot topic in neuroscience in the 1990s when the studies of the visual system of the brain by Gray, Singer and others appeared to support the neural binding hypothesis.[74] According to this idea, synchronous oscillations in neuronal ensembles bind neurons representing different features of an object. For example, when a person looks at a tree, visual cortex neurons representing the tree trunk and those representing the branches of the same tree would oscillate in synchrony to form a single representation of the tree. This phenomenon is best seen in local field potentials which reflect the synchronous activity of local groups of neurons, but has also been shown in EEG and MEG recordings providing increasing evidence for a close relation between synchronous oscillatory activity and a variety of cognitive functions such as perceptual grouping[73] and attentional top-down control.[15][13][12] PacemakerCells in the sinoatrial node, located in the right atrium of the heart, spontaneously depolarize approximately 100 times per minute. Although all of the heart's cells have the ability to generate action potentials that trigger cardiac contraction, the sinoatrial node normally initiates it, simply because it generates impulses slightly faster than the other areas. Hence, these cells generate the normal sinus rhythm and are called pacemaker cells as they directly control the heart rate. In the absence of extrinsic neural and hormonal control, cells in the SA node will rhythmically discharge. The sinoatrial node is richly innervated by the autonomic nervous system, which up or down regulates the spontaneous firing frequency of the pacemaker cells. Central pattern generatorSynchronized firing of neurons also forms the basis of periodic motor commands for rhythmic movements. These rhythmic outputs are produced by a group of interacting neurons that form a network, called a central pattern generator. Central pattern generators are neuronal circuits that—when activated—can produce rhythmic motor patterns in the absence of sensory or descending inputs that carry specific timing information. Examples are walking, breathing, and swimming,[75] Most evidence for central pattern generators comes from lower animals, such as the lamprey, but there is also evidence for spinal central pattern generators in humans.[76][77] Information processingNeuronal spiking is generally considered the basis for information transfer in the brain. For such a transfer, information needs to be coded in a spiking pattern. Different types of coding schemes have been proposed, such as rate coding and temporal coding. Neural oscillations could create periodic time windows in which input spikes have larger effect on neurons, thereby providing a mechanism for decoding temporal codes.[78] Temporal decodingSingle-cell intrinsic oscillators serve as valuable tools for decoding temporally-encoded sensory information. This information is encoded through inter-spike intervals, and intrinsic oscillators can act as 'temporal rulers' for precisely measuring these intervals. One notable mechanism for achieving this is the neuronal phase-locked loop (NPLL). In this mechanism, cortical oscillators undergo modulation influenced by the firing rates of thalamocortical 'phase detectors,' which, in turn, gauge the disparity between the cortical and sensory periodicity.[79] PerceptionSynchronization of neuronal firing may serve as a means to group spatially segregated neurons that respond to the same stimulus in order to bind these responses for further joint processing, i.e. to exploit temporal synchrony to encode relations. Purely theoretical formulations of the binding-by-synchrony hypothesis were proposed first,[80] but subsequently extensive experimental evidence has been reported supporting the potential role of synchrony as a relational code.[81] The functional role of synchronized oscillatory activity in the brain was mainly established in experiments performed on awake kittens with multiple electrodes implanted in the visual cortex. These experiments showed that groups of spatially segregated neurons engage in synchronous oscillatory activity when activated by visual stimuli. The frequency of these oscillations was in the range of 40 Hz and differed from the periodic activation induced by the grating, suggesting that the oscillations and their synchronization were due to internal neuronal interactions.[81] Similar findings were shown in parallel by the group of Eckhorn, providing further evidence for the functional role of neural synchronization in feature binding.[82] Since then, numerous studies have replicated these findings and extended them to different modalities such as EEG, providing extensive evidence of the functional role of gamma oscillations in visual perception. Gilles Laurent and colleagues showed that oscillatory synchronization has an important functional role in odor perception. Perceiving different odors leads to different subsets of neurons firing on different sets of oscillatory cycles.[83] These oscillations can be disrupted by GABA blocker picrotoxin,[84] and the disruption of the oscillatory synchronization leads to impairment of behavioral discrimination of chemically similar odorants in bees,[85] and to more similar responses across odors in downstream β-lobe neurons.[86] Recent follow-up of this work has shown that oscillations create periodic integration windows for Kenyon cells in the insect mushroom body, such that incoming spikes from the antennal lobe are more effective in activating Kenyon cells only at specific phases of the oscillatory cycle.[78] Neural oscillations are also thought be involved in the sense of time[87] and in somatosensory perception.[88] However, recent findings argue against a clock-like function of cortical gamma oscillations.[89] Motor coordinationOscillations have been commonly reported in the motor system. Pfurtscheller and colleagues found a reduction in alpha (8–12 Hz) and beta (13–30 Hz) oscillations in EEG activity when subjects made a movement.[62][90] Using intra-cortical recordings, similar changes in oscillatory activity were found in the motor cortex when the monkeys performed motor acts that required significant attention.[91][92] In addition, oscillations at spinal level become synchronised to beta oscillations in the motor cortex during constant muscle activation, as determined by cortico-muscular coherence.[93][94][95] Likewise, muscle activity of different muscles reveals inter-muscular coherence at multiple distinct frequencies reflecting the underlying neural circuitry involved in motor coordination.[96][97] Recently it was found that cortical oscillations propagate as travelling waves across the surface of the motor cortex along dominant spatial axes characteristic of the local circuitry of the motor cortex.[98] It has been proposed that motor commands in the form of travelling waves can be spatially filtered by the descending fibres to selectively control muscle force.[99] Simulations have shown that ongoing wave activity in cortex can elicit steady muscle force with physiological levels of EEG-EMG coherence.[100] Oscillatory rhythms at 10 Hz have been recorded in a brain area called the inferior olive, which is associated with the cerebellum.[20] These oscillations are also observed in motor output of physiological tremor[101] and when performing slow finger movements.[102] These findings may indicate that the human brain controls continuous movements intermittently. In support, it was shown that these movement discontinuities are directly correlated to oscillatory activity in a cerebello-thalamo-cortical loop, which may represent a neural mechanism for the intermittent motor control.[103] MemoryNeural oscillations, in particular theta activity, are extensively linked to memory function. Theta rhythms are very strong in rodent hippocampi and entorhinal cortex during learning and memory retrieval, and they are believed to be vital to the induction of long-term potentiation, a potential cellular mechanism for learning and memory. Coupling between theta and gamma activity is thought to be vital for memory functions, including episodic memory.[104][105] Tight coordination of single-neuron spikes with local theta oscillations is linked to successful memory formation in humans, as more stereotyped spiking predicts better memory.[106] Sleep and consciousnessSleep is a naturally recurring state characterized by reduced or absent consciousness and proceeds in cycles of rapid eye movement (REM) and non-rapid eye movement (NREM) sleep. Sleep stages are characterized by spectral content of EEG: for instance, stage N1 refers to the transition of the brain from alpha waves (common in the awake state) to theta waves, whereas stage N3 (deep or slow-wave sleep) is characterized by the presence of delta waves.[107] The normal order of sleep stages is N1 → N2 → N3 → N2 → REM.[citation needed] DevelopmentNeural oscillations may play a role in neural development. For example, retinal waves are thought to have properties that define early connectivity of circuits and synapses between cells in the retina.[108] Pathology 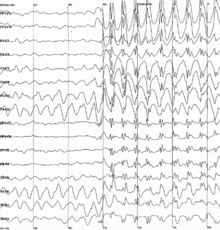 Specific types of neural oscillations may also appear in pathological situations, such as Parkinson's disease or epilepsy. These pathological oscillations often consist of an aberrant version of a normal oscillation. For example, one of the best known types is the spike and wave oscillation, which is typical of generalized or absence epileptic seizures, and which resembles normal sleep spindle oscillations. TremorA tremor is an involuntary, somewhat rhythmic, muscle contraction and relaxation involving to-and-fro movements of one or more body parts. It is the most common of all involuntary movements and can affect the hands, arms, eyes, face, head, vocal cords, trunk, and legs. Most tremors occur in the hands. In some people, tremor is a symptom of another neurological disorder. Many different forms of tremor have been identified, such as essential tremor or Parkinsonian tremor. It is argued that tremors are likely to be multifactorial in origin, with contributions from neural oscillations in the central nervous systems, but also from peripheral mechanisms such as reflex loop resonances.[109] EpilepsyEpilepsy is a common chronic neurological disorder characterized by seizures. These seizures are transient signs and/or symptoms of abnormal, excessive or hypersynchronous neuronal activity in the brain.[110] Thalamocortical dysrhythmiaIn thalamocortical dysrhythmia (TCD), normal thalamocortical resonance is disrupted. The thalamic loss of input allows the frequency of the thalamo-cortical column to slow into the theta or delta band as identified by MEG and EEG by machine learning.[111] TCD can be treated with neurosurgical methods like thalamotomy. ApplicationsClinical endpointsNeural oscillations are sensitive to several drugs influencing brain activity; accordingly, biomarkers based on neural oscillations are emerging as secondary endpoints in clinical trials and in quantifying effects in pre-clinical studies. These biomarkers are often named "EEG biomarkers" or "Neurophysiological Biomarkers" and are quantified using quantitative electroencephalography (qEEG). EEG biomarkers can be extracted from the EEG using the open-source Neurophysiological Biomarker Toolbox. Brain–computer interfaceNeural oscillation has been applied as a control signal in various brain–computer interfaces (BCIs).[112] For example, a non-invasive BCI can be created by placing electrodes on the scalp and then measuring the weak electric signals. Although individual neuron activities cannot be recorded through non-invasive BCI because the skull damps and blurs the electromagnetic signals, oscillatory activity can still be reliably detected. The BCI was introduced by Vidal in 1973[113] as challenge of using EEG signals to control objects outside human body. After the BCI challenge, in 1988, alpha rhythm was used in a brain rhythm based BCI for control of a physical object, a robot.[114][115] Alpha rhythm based BCI was the first BCI for control of a robot.[116][117] In particular, some forms of BCI allow users to control a device by measuring the amplitude of oscillatory activity in specific frequency bands, including mu and beta rhythms. ExamplesA non-inclusive list of types of oscillatory activity found in the central nervous system:
See also
References
Further reading
External links |