|
Dominante StrategieDie dominante Strategie in spieltheoretischen Modellen ist eine Strategie, die unter allen möglichen Strategien den höchsten Nutzen bietet, unabhängig davon, was die anderen Akteure (Spieler, Agenten) tun. Das Konzept der dominanten Strategie erscheint sowohl in der klassischen Entscheidungstheorie als auch in der Spieltheorie und erlaubt es, Verhaltensweisen von Akteuren in einem Spiel zu erkennen.[1] Die dominante Strategie findet in simultanen, wie auch sequenziellen Spielen Anwendung. AbgrenzungDie dominierte Strategie stellt im Gegensatz zur dominanten Strategie eine der schlechtesten Strategien dar. Wiederum unabhängig davon, was die anderen Akteure tun, wird die dominierte Strategie von einer stets besseren, der sogenannten dominanten Strategie, dominiert.[2] Die dominierte Strategie eines Spielers stellt für diesen keinen Nutzen dar und findet auch wiederum keine streng beste Antwort auf keine Strategie des Gegenspielers.[3] Stellt man die dominierte Strategie der dominanten Strategie gegenüber, wird deutlich, dass die dominante Strategie immer durchgehend besser ist als jede andere Strategie. Hingegen ist die dominierte Strategie immer durchgehend schlechter als alle anderen Strategien.[4] Eine Entfernung der dominierten Strategie(n) ist demnach vorzunehmen. BegriffsdefinitionDer Begriff der dominanten Strategie benennt eine Abfolge von Handlungen, die besser ist, als alle anderen Möglichkeiten, unabhängig davon, was die anderen Akteure tun.[5] Wodurch eine Strategie eine andere Strategie dominiert, wenn die dominierende nie schlechter, jedoch manchmal besser als die dominierte Strategie ist.[6] Ein rationaler Akteur sollte keine Strategie wählen, wenn eine alternative Strategie existiert, welche zu einem höheren Nutzen führt gegenüber allen möglichen Strategien. Wenn es eine dominante Strategie gibt, so ist diese anzuwenden. Jedoch haben nicht immer alle Akteure eine dominante Strategie, nicht einmal für einen der Akteure. Die Dominanz ist die Ausnahme und nicht die Regel.[4] Methodik der dominanten StrategieAnwendungIm Gegensatz zum sequenziellen Spiel ist ein simultanes Spiel durch mangelnde Kommunikation der exogenen Faktoren innerhalb eines Spieles gekennzeichnet. Es kann nur einmal gespielt werden. Hingegen sind bei einem sequenziellen Spiel die Schritte des Gegners im Normalfall bekannt. Dies ist durch Kommunikation gewährleistet, obgleich dennoch eine gewisse Informationsasymmetrie vorliegen kann. Wenn demnach eine dominante Strategie für jede gegebene Entscheidung ihres Gegners vorliegt, so würde bei sequenziellen Zügen stets die dominante Strategie gewählt werden. Jedoch könnte hier genauso der umgedrehte Fall auftreten, wodurch der Gegner erst im zweiten Zug an der Reihe ist. Hier kann der Gegner in aller Ruhe die Entscheidung abwarten und diese an die Situation anpassen. Hier empfiehlt es sich eine andere als die dominante Strategie zu wählen. Man spricht in diesem Fall von Selbstbindung auf spieltheoretischer Basis.[7] Bei sequenziellen Zügen kann unter Anwendung von dominanten Strategien in der Spieltheorie ebenfalls die Anwendung von Kooperationslösungen in Betracht gezogen werden. Streng/strikt dominante StrategieEine Strategie eines Spielers ist eine streng dominante Strategie, wenn sie bei allen möglichen Strategiekombinationen seiner Mitspieler für ihn einen größeren Nutzen hat, als alle seine anderen Strategien. Da diese Eigenschaft nur jeweils auf eine Strategie zutreffen kann, gibt es für jeden Spieler höchstens eine streng dominante Strategie. Ein Spieler mit einer streng dominanten Strategie muss nicht kooperieren, um für sich den größten Nutzen zu erzielen. Die Bedingung für eine streng dominante Strategie lässt sich durch eine mathematische Formel beschreiben. Seien die möglichen Strategien eines Spielers und die möglichen Strategiekombinationen seiner Mitspieler. Eine Strategie des Spielers heißt streng dominant, wenn für alle anderen Strategien des Spielers und alle Strategiekombinationen seiner Mitspieler gilt. Dabei bedeutet , dass Spieler die linke Strategiekombination höher bewertet als die rechte. Gibt es in einem Spiel eine Nutzenfunktion und hat ein Spieler eine streng dominante Strategie, dann ist diese Strategie diejenige mit der höchsten Auszahlung für ihn. AnwendungsbeispielDas Szenario in Abbildung 1 stellt die beiden konkurrierenden Sportartikelhersteller Nike und Adidas dar, die je nach Entscheidungsstrategie ihren Umsatz durch möglicherweise mehr Einsatz von Werbung verändern könnten. Das Ziel beider besteht hierbei in der Maximierung des Umsatzes. 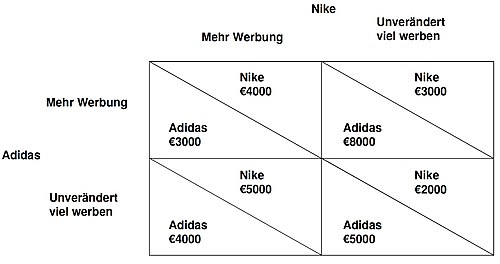 Für Nike ist es in jedem Fall besser, mehr Werbung zu investieren, um den Umsatz zu steigern: Investiert Adidas auch in mehr Werbung, so erzielt Nike trotzdem noch einen erhöhten Umsatz von 4000 Euro. Wenn Adidas allerdings unverändert viel Werbung einsetzt, so erzielt Nike sogar einen noch höheren Umsatz von 5000 Euro. Nike könnte sich allerdings auch für unverändert viel Werbung entscheiden, würde jedoch demnach einen niedrigeren Umsatz in Kauf nehmen als bei dem Einsatz von mehr Werbung. Egal, was Adidas tut: Für Nike ist es in jedem Fall besser, mehr Werbung zu investieren. Die Strategie mehr Werbung ist für Nike die streng beste Antwort auf jede denkbare Strategie von Adidas. Dabei wird die Alternative gleich viel Werbung von der Alternative mehr Werbung dominiert. Die Alternative mehr Werbung ist für Nike demnach eine streng dominante Strategie. Schwach dominante StrategieEine Strategie eines Spielers ist eine schwach dominante Strategie, wenn sie bei allen möglichen Strategiekombinationen seiner Mitspieler für ihn den größten Nutzen hat. Im Allgemeinen kann ein Spieler mehrere dominante Strategien haben, die dann für ihn alle den gleichen Nutzen haben. Ein Spieler mit einer schwach dominanten Strategie muss nicht kooperieren, um für sich den größten Nutzen zu erzielen. Die Bedingung für eine schwach dominante Strategie lässt sich durch eine mathematische Formel beschreiben. Eine Strategie eines Spielers heißt schwach dominant, wenn für alle anderen Strategien des Spielers und alle Strategiekombinationen seiner Mitspieler und für mindestens eine dieser Strategiekombination gilt. Dabei bedeutet , dass Spieler die linke Strategiekombination mindestens genauso hoch bewertet wie die rechte. Gibt es in einem Spiel eine Nutzenfunktion und hat ein Spieler schwach dominante Strategien, dann haben diese Strategien die höchsten Auszahlung für ihn. AnwendungsbeispielDas in der Abbildung 2 dargestellte Szenario des Gefangenendilemmas beruht auf zwei Angeklagten, die ein Verbrechen tatsächlich begangen haben. Die Freiheitsstrafen können je nach Entscheidungsstrategie unterschiedlich sein. Es handelt sich hierbei um ein simultanes Spiel, in dem die Angeklagten nicht dazu berechtigt sind, von der Entscheidung des jeweils Anderen in Erfahrung gesetzt zu werden. Das Ziel beider besteht hierbei in der Minimierung der eigenen Haftstrafe. 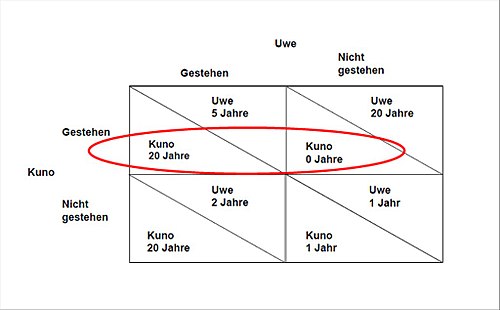 Es lässt sich feststellen, dass für Kuno keine streng dominante Strategie existiert: Würde Uwe nicht gestehen, so wäre es für Kuno am besten, zu gestehen. Wählt Uwe gestehen, dann sind für Kuno beide Strategien gleich gut. Kuno ist indifferent zwischen gestehen und nicht gestehen. Es lässt sich also feststellen, dass für Kuno die Strategie zu gestehen nie schlechter ist als die Strategie nicht zu gestehen; im Falle, dass Uwe nicht gesteht, sogar besser. Nach Identifizierung der schwach dominierten Strategie nicht gestehen kann also angenommen werden, dass Kuno gestehen wird. Lösungskonzepte in dominanten StrategienDie dominante Strategie stellt in der Spieltheorie ein Lösungskonzept dar. Verfügt in einem Spiel jeder Spieler über eine streng dominante Strategie, so ist es für jeden Spieler rational diese Strategiekonfiguration als nicht-kooperative Lösung zu spielen. Jedoch garantiert dies nicht, dass die resultierenden Auszahlungen ebenso kollektiv rational sind.[8] Durch die Zusammensetzung der rational gewählten Strategiekombination befindet sich das Spiel in einem Gleichgewicht dominanter Strategien. Jedes Gleichgewicht dominanter Strategien macht ebenso gleichzeitig ein Nash-Gleichgewicht sichtbar. Eine weitere Lösung eines Spieles in der Spieltheorie mit dominanten Strategien stellt die Eliminierung der dominierten Strategien dar. Obgleich die dominierte Strategie keinen Nutzen für den jeweiligen Spieler darstellt, so ergibt sich doch hieraus eine Möglichkeit die Komplexität eines Spieles zu reduzieren. Demnach kann die Anzahl der möglichen Spielergebnisse unter Anwendung der Iterative Elimination strikt dominierter Strategien die Anzahl der möglichen Spielergebnisse einschränken.[9] Die Wahl der nutzenmaximierenden Strategie wird dadurch erleichtert. Literatur
WeblinksEinzelnachweise
|












