|
Assoziation (UML)Eine Assoziation (englisch association) ist ein Modellelement in der Unified Modeling Language (UML[1]), einer Modellierungssprache für Software und andere Systeme. 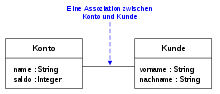  Eine Assoziation beschreibt eine Beziehung zwischen zwei oder mehr Classifiern, im häufigsten Fall eine Verbindung zwischen genau zwei Klassen. Assoziationen definieren dabei eine Beziehung auf Typebene. Auf Instanzebene nennen sich die konkreten Ausprägungen einer Assoziation Link. Neben Klassen können aber auch beliebige andere Classifier (beispielsweise Schnittstellen oder Anwendungsfälle) mittels Assoziationen in Beziehung zueinander gesetzt werden. Die Möglichkeit, mehr als zwei Typen an einer Assoziation zu beteiligen, wird eher selten genutzt. Die Assoziation wird in diesem Fall n-äre Assoziation genannt und durch eine Raute, an der n zu den Objekten führende Linien anliegen, dargestellt. Die Assoziation in UML ist mit dem Relationship-Typ im Entity-Relationship-Modell vergleichbar, wobei hier Detailunterschiede bestehen, die zwar auf den ersten Blick nicht ohne weiteres erkennbar, in der Praxis aber von großer Bedeutung sind (siehe Object-relational impedance mismatch). Prinzipiell erlaubt, wenn auch nicht üblich, ist die Darstellung mit Raute auch bei Assoziationen mit nur zwei Assoziationsenden, wodurch das Erscheinungsbild der Chen-Notation von Entity-Relationship-Modellen ähnelt. Eine Assoziation heißt reflexiv, wenn sie einen Classifier mit sich selbst verbindet. Die beiden Enden der Assoziation zeigen hier also auf den gleichen Typ. In der Abbildung rechts ist die Assoziation „Elternteil/Kind-Beziehung“ reflexiv. AssoziationsendenGrafisch wird eine Assoziation durch eine Linie dargestellt. Hierbei wird unterschlagen, dass die Enden einer Assoziation nicht einfach grafische Punkte, sondern eigenständige Modellelemente sind. Im Unterschied zur UML 1.4 gibt es aber kein Modellelement Assoziationsende (englisch association end) mehr, denn das Ende einer Assoziation wird seit UML2 mit dem Modellelement Eigenschaft (englisch property) modelliert.  In der Abbildung rechts ist an einem Beispiel gezeigt, dass das Repository-Modell hinter dem Klassendiagramm ein Assoziationsende als Instanz der Metaklasse Property speichert. Assoziationsenden können deshalb alle Merkmale einer Eigenschaft haben:
 Eine Assoziation bildet eine Art Brücke zwischen zwei Typen: startet man bei der Instanz des einen beteiligten Typs, kann man über eine Objektbeziehung zur Instanz des zweiten Typs mit Leichtigkeit navigieren. Die andere Richtung ist nicht verboten, aber es könnte aufwändig sein. Die UML2 erlaubt nun, die Navigierbarkeit von Assoziationsenden einzuschränken. Dabei unterscheidet sie drei Arten, wie die Navigierbarkeit festgelegt werden kann:
Assoziationen, die auf beiden Seiten navigierbar sind, heißen bidirektionale Assoziationen, nur an einem Ende navigierbare Assoziationen entsprechend unidirektional.  Das Beispiel links zeigt zwei Assoziationen zwischen den gleichen Typen. Weil sie unterschiedliche Namen Aggregation und Komposition Möchte man nun ein Assoziationsende hervorheben oder die Bindung einer Assoziation verstärken, so stehen einem Aggregation und Komposition als Mittel zur Verfügung. Dies sind Spezialfälle der Assoziation – es gibt Assoziationen, die weder Aggregation noch Komposition sind. In der grafischen Darstellung einer Aggregation kennzeichnet eine nicht ausgefüllte Raute das Ende, das mit dem Ganzen verbunden ist. Im Sonderfall der Komposition ist es eine ausgefüllte Raute. AggregationDie Aggregation, sowie auch die Komposition, ist eine Assoziation von Teilen zu einem Ganzen. Jedes Teil ist zu dem Ganzen mit einer Assoziation „ist-teil-von“ (englisch is-part-of) verbunden. Eine exakte Definition wird in der UML2 nicht gegeben, vielmehr wird darauf verwiesen, dass eine Aggregation je nach Anwendung und Modellierer variiert. Ein konkreter Nutzen lässt sich z. B. ableiten, indem man einem Ende einer Assoziation eine besondere Betonung zukommen lässt. Eine Aggregation ist, normalerweise, homöomer, d. h., alle Bestandteile des Ganzen sind vom gleichen Typ. So besteht eine Klasse aus Studenten oder ein Text aus Paragraphen. Grundsätzlich ist die Abgrenzung zwischen Assoziation und Aggregation schwierig. Ein schwaches Indiz für die sinnvolle Verwendung einer Aggregation scheint das Vorliegen von Transitivitäten zwischen den modellierten Klassen zu sein. Das heißt, wenn zwischen A und B eine Teil-Ganzes-Beziehung existiert und zwischen B und C ebenfalls, dann muss A auch ein Teil von C sein. Ein weiteres Indiz könnte die Kaskadierung von Verhalten vom Ganzen zu den Teilen sein: Eine für das Ganze definierte Operation ist so zu implementieren, dass sie die gleiche Operation auf all seinen Teilen aufruft. Dass man nicht spezifizieren kann, welche Operation das sein soll, verdankt die Aggregation wohl ihren Status als unverbindliche Absichtserklärung. Eine spezielle Art der Aggregation ist die Komposition. KompositionDie Komposition (englisch composite aggregation oder englisch composition) als Sonderfall der Aggregation beschreibt ebenfalls die Beziehung zwischen einem Ganzen und seinen Teilen. Der Unterschied zur Aggregation ist, dass die Teile, die ein Objekt enthält, von dem Ganzen existentiell abhängig sind. Die Komposition ist, im Gegensatz zur Aggregierung, meistens heteromer, d. h. die Bestandteile eines Ganzen sind von verschiedenen Typen. So besteht ein Auto aus Motor, Karosserie und Rädern. Ein Objekt kann dabei immer nur Teil genau keines oder eines Ganzen sein (Multiplizität 0 oder 1). Die Beziehung zwischen einem Raum-Softwareobjekt und einem Gebäude-Softwareobjekt könnte als Komposition betrachtet werden: Ein Raum ist zu jedem Zeitpunkt ein Teil genau eines Gebäudes. Existentielle Abhängigkeit bedeutet, dass das Ganze die Lebensdauer der Teile bestimmt. Wird das Ganze gelöscht, verschwinden auch die Objekte, die zu diesem Zeitpunkt Bestandteil waren. Das bei der Aggregation noch unbestimmte kaskadierende Verhalten ist bei der Komposition also das Löschen. Wird das Gebäude-Softwareobjekt aus der Applikation gelöscht, kann es sinnvoll sein, auch die enthaltenen Raum-Softwareobjekte zu löschen. Die Komposition macht genau dies mit den Raum-Softwareobjekten. Achtung: In einer Applikation kann es durchaus sinnvoll sein, die Raum-Softwareobjekte zu behalten. In einer Tourmanagementapplikation werden zum Beispiel die Gebäude des letzten Veranstaltungsorts gelöscht, die verschiedenen Räume für die Diva (Entspannungsraum vor dem Konzert, Musikzimmer, Garderobe und Suite) bleiben aber, weil sie in der nächsten Stadt wieder Gebäuden zugeordnet werden müssen. Dann sollte man natürlich keine Komposition verwenden. Ein reales Gebäude besteht aus Steinen. Diese Steine verschwinden nicht, wenn das Gebäude abgerissen wird. Dass die realen Räume danach nicht mehr da sind, hat den gleichen Grund wie beim Gebäude: Ihre Existenz setzt einen gewissen Zusammenhalt der Steine voraus. Eine Komposition beschreibt einen azyklischen gerichteten Graph (). Als Relation ist sie asymmetrisch und transitiv. Unterschiede zur UML 1.4Die UML2 hat die Notation für die Navigierbarkeit von Assoziationsenden eingeführt. In der UML 1.4 gab es ein spezielles Modellelement AssociationEnd, das in der UML2 durch Property ersetzt wurde. Siehe auchEinzelnachweise
|

