|
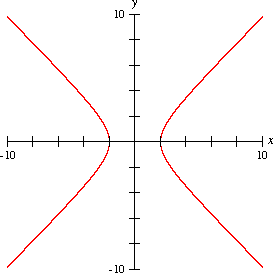
Hipèrbola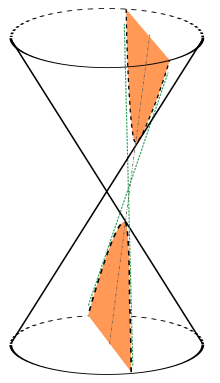 Una hipèrbola o hipèrbole es defineix com el lloc geomètric dels punts del pla per als quals és constant la diferència de les distàncies a dos punts fixos denominats focus. La forma més freqüent d'una hipèrbola és la següent: La hipèrbola és la corba cònica oberta formada dues branques resultat de la intersecció de les dues parts d'una superfície cònica amb un pla que la talla i que forma amb l’eix del con un angle més petit que amb la generatriu del con. És habitual pensar que cal que el pla sigui paral·lel a l'eix, però no és així i a més, en tots els casos, les dues branques de la hipèrbola són simètriques.[1] AsímptotesUna asímptota és una recta que, en prolongar-la indefinidament, s'acosta cada vegada més a la gràfica de la corba, però no arriba mai a tocar-la. Això passa perquè en les asímptotes les gràfiques no existeixen. Continuïtat i discontinuïtatLes representacions d'hipèrboles poden ser diferents, ja siguin contínues o discontínues. La diferència és que quan es podrà representar sense aixecar el llapis del paper la gràfica serà contínua i quan s'hagi d'aixecar el llapis del paper per força serà discontínua Equacions de la hipèrbolaEquacions en coordenades cartesianes
on a i b són els semieixos major i menor.
on és el centre Equacions en coordenades polarsEquacions paramètriquesRepresentació d'hipèrbolesDominiPer a cercar el domini el que cal fer és trobar tots els nombres que facin que equació no tengui solució. En aquest cas el domini seria: (Això vol dir que el domini seria tots els nombres reals menys quan X=2 perquè seria 3 dividit 0 i no es pot dividir per 0 en cap cas. AsímptotesLes asímptotes són rectes verticals per on no passa la funció, és a dir, seria el nombre del domini. En aquest cas (2). Punts de tallEls punts de tall de les ens indiquen per on passa la gràfica quan . El punt de tall de la ens indica per on passa la gràfica quan Per saber els punts de tall en les X hem de donar valor 0 a la Y. hi hem de resoldre l'equació. En el cas del punt de tall de la Y hem de donar 0 al valor de la X. hi hem de resoldre la divisió. Signe de la funcióPer saber el signe de la funció en cada tram, els valors de la X han de ser les asímptotes i els nombres dels punts de talls de les x. Entre nombre i nombre heu d'agafar un nombre intermedi i substituir el nombre per la x i observar el signe. El signe ens indicarà el signe de la gràfica entre aquells dos intervals. Vegeu tambéReferències
|