|
Àlgebra homològicaL'àlgebra homològica[1] és una noció bàsica de la topologia algebraica. Intuïtivament, dues corbes en un pla o una altra superfície bidimensional són homòlogues si juntes delimiten una regió -definint així un dins i un fora. De manera similar, dues superfícies en un espai tridimensional són homòlogues si entre elles delimiten una regió de l'espai.[2]  Més formalment, l'àlgebra homològica és la branca de les matemàtiques que estudia l'homologia en un context algebraic general. Té els seus orígens en les investigacions sobre topologia combinatòria (una precursora de la topologia algebraica) i l'àlgebra abstracta (teoria de mòduls i syzygys) al final del segle xix, principalment degudes a Henri Poincaré i David Hilbert. El desenvolupament de l'àlgebra homològica està íntimament relacionat amb el sorgiment de la teoria de categories. De fet, l'àlgebra homològica és l'estudi dels functors homològics i les estructures algebraiques intricades que conté. Un concepte útil i freqüent en matemàtiques és el dels complexos de cadenes, que es poden estudiar tant a través de la seva homologia com de la seva cohomologia. L'àlgebra homològica proporciona les eines per extreure la informació continguda en aquests complexos, i presentar-la en la forma d'invariants d'anells, mòduls, espais topològics i altres objectes matemàtics. Una eina potent per realitzar aquesta anàlisi la proporcionen les successions espectrals. Des del seu origen, l'àlgebra homològica ha jugat un rol important en topologia algebraica. El seu àmbit d'influència ha crescut amb el temps, i actualment inclou l'àlgebra commutativa, la geometria algebraica, la teoria de nombres algebraics, la teoria de representació, la física matemàtica, les àlgebres d'operadors, l'anàlisi complexa i la teoria d'equacions en derivades parcials. Història de l'àlgebra homològicaL'àlgebra homològica començà a ser estudiada en la seva forma més bàsica durant el segle xix com a part de la topologia, però no va ser fins a la dècada de 1940 que esdevingué una àrea independent amb l'estudi d'objectes tals com el functor Ext i el functor Tor, entre altres.[3] Complexos de cadenes i homologiaEl complex de cadenes és la noció central de l'àlgebra homològica. És una successió de grups abelians i homomorfismes de grups, amb la propietat que la composició de dos homomorfismes consecutius qualssevol és zero: Els elements de Cn s'anomenen n-cadenes i els homomorfismes dn s'anomenen diferencials.[4] Els grups Cn es poden dotar d'una estructura addicional; per exemple, poden ser espais vectorials o mòduls sobre un anell fixat R. Les diferencials han de preservar aquesta estructura addicional, en el cas que existeixi; per exemple, han de ser aplicacions lineals o homomorfismes de R-mòduls. Per convenció, ens restingirem al cas de grups abelians (estrictament, a la categoria Ab de grups abelians; un famós teorema de Barry Mitchell assegura que els resultats són vàlids en el cas general d'una categoria abeliana qualsevol). Tot complex de cadenes defineix altres dues successions de grups abelians, els cicles Zn = Ker dn i les fronteres Bn = Im dn+1, on Ker d i Im d simbolitzen el nucli i la imatge de d, respectivament. Com que la composició de dues diferencials qualssevol és zero, aquests grups estan submergits l'un en l'altre:
Els subgrups dels grups abelians són automàticament normals; per tant, poden definir l'n-sim grup d'homologia Hn(C) com el grup quocient dels n-cicles per les n-fronteres,
Hom diu que un complex de cadenes és acíclic o que és una successió exacta si tots els seus grups d'homologia són zero. Els complexos de cadenes sorgeixen freqüentment en àlgebra i topologia algebraica. Per exemple, si X és un espai topològic, llavors les cadenes singulars Cn(X) són combinacions lineals formals de funcions contínues del n-símplex estàndard cap a X; si K és un complex simplicial, llavors les cadenes simplicials Cn(K) són combinacions lineals formals dels n-símplexs de X; si A = F/R és una presentació d'un grup abelià A per generadors i relacions, on F és un grup abelià lliure generat pels generadors i R és el subgrup de relacions, llavors escrivint C1(A) = R, C0(A) = F, i Cn(A) = 0 per a qualsevol altre n obtenim una successió de grups abelians. En tots aquests casos, existeixen diferencials naturals dn que converteixen Cn en un complex de cadenes, l'homologia dels quals reflecteixen l'estructura de l'espai topològic X, del complex simplicial K o del grup abelià A. En el cas d'espais topològics, arribem a la noció d'homologia singular, que juga un rol fonamental en la investigació de les propietats d'aquests espais, com per exemple les varietats. Des d'un punt de vista filosòfic, l'àlgebra homològica mostra que certs complexos de cadenes associats amb objectes algebraics o geomètrics (espais topològics, complexos simplicials, R-mòduls) contenen molta informació valuosa sobre ells, i l'homologia és la que es pot copsar més fàcilment. Des d'un punt de vista tècnic, l'àlgebra homològica ens proporciona les eines per a manipular complexos i extreure'n aquesta informació. Per exemple:
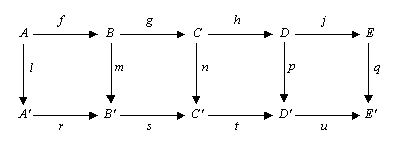
Eines i tècniquesSuccessions exactesEn el context de la teoria de grups, una successió de grups i homomorfismes de grups s'anomena exacta si la imatge de cada homomorfisme és igual al nucli del següent:
Notem que la successió de grups i homomorfismes pot ser finita o infinita. Hom pot establir una definició similar per a altres estructures algebraiques. Per exemple, podríem tenir una successió exacta d'espais vectorials i aplicacions lineals, o de mòduls i homomorfismes de mòduls. Més en general, la noció d'una successió exacta té sentit en qualsevol categoria amb nuclis i conuclis. Successió exacta curtaEl tipus més comú de successió exacta és la successió exacta curta. És una successió exacta de la forma on f és un monomorfisme i g és un epimorfisme. En aquest cas, A és un subobjecte de B, i el quocient corresponent és isomorf a C: (on f(A) = im(f)). Una successió exacta curta de grups abelians també es pot escriure com una successió exacta amb 5 termes: on 0 representa l'objecte zero, com el grup trivial o un espai vectorial 0-dimensional. El fet de col·locar els objectes zero obliga a què f sigui un monomorfisme i a què g sigui un epimorfisme. Successió exacta llargaUna successió exacta llarga és una successió exacta indexada pels nombres naturals. El lema dels cincConsiderem el següent diagrama commutatiu en qualsevol categoria abeliana (com per exemple la categoria dels grups abelians o la categoria d'espais vectorials sobre un cos donat), o la categoria dels grups. El lema dels cinc afirma que, si les files són exactes, m i p són isomorfismes, l és un epimorfisme, i q és un monomorfisme, llavors n també és un isomorfisme. El lema de la serpEn una categoria abeliana (com per exemple la categoria dels grups abelians o la categoria dels espais vectorials sobre un cos donat), considerem un diagrama commutatiu: on les files són successions exactes i 0 és l'objecte zero. Llavors existeis una successió exacta que relaciona els nuclis i els conuclis de a, b i c: Addicionalment, si el morfisme f és un monomorfisme, llavors també ho és el morfisme ker a → ker b, i si g és un epimorfisme, llavors també ho és coker b → coker c. Categories abelianesEn matemàtiques, una categoria abeliana és una categoria en la qual els morfismes i els objectes es poden sumar, i en la qual existeixen nuclis i conuclis, i tenen propietats desitjables. L'exemple per antonomàsia d'una categoria abeliana és la categoria dels grups abelians, Ab. La teoria sorgí com un intent d'unificar diverses teories de cohomologia d'Alexander Grothendieck. Les categories abelianes són força estables; per exemple, són regulars i satisfan el lema de la serp. La classe de les categories abelianes és tancada per diverses construccions de categories, per exemple la categoria de complexos de cadenes d'una categoria abeliana, o la categoria de functors d'una categoria menor cap a una categoria abeliana són també abelianes. Aquestes propietats d'estabilitat fan que s'utilitzin a bastament en àlgebra homològica i en altres àmbits: la teoria té aplicacions importants en geometria algebraica, cohomologia i teoria de categories pura. Les categories abelianes reben aquest nom per Niels Henrik Abel. Més concretament, una categoria és abeliana si
Functor ExtSigui R un anell, i sigui ModR la categoria dels mòduls sobre R. Sigui B un mòdul de ModR, i escrivim T(B) = HomR(A,B), per a un A de ModR fixat. Això és un functor exacte esquerre i, per tant, té functors derivats RnT. Hom defineix el functor Ext com
Això es pot calcular prenent qualsevol resolució injectiva
i calculant
Llavors (RnT)(B) és l'homologia d'aquest complex. Notem que HomR(A,B) està exclosa del complex. Hom pot proporcionar una definició alternativa, emprant el functor G(A)=HomR(A,B). Per a un mòdul B fixat, això és un functor exacte esquerre contravariant i, per tant, també tenim functors derivats per la dreta RnG, i podem definir
Això es pot calcular escollint una resolució projectiva qualsevol
i procedir amb els duals, calculant
Llavors (RnG)(A) és l'homologia d'aquest complex. Notem, de nou, que s'exclou HomR(A,B). Aquestes dues construccions proporcionen resultats isomorfs i, per tant, qualsevol de les dues es pot fer servir per a calcular el functor Ext. Functor TorSuposem que R és un anell, i denotem per R-Mod la cateogira de R-mòduls per l'esquerra, i per Mod-R la categoria de R-mòduls per la dreta (si R és commutatiu, les dues categories coincideixen). Prenem un mòdul B fixat de R-Mod. Per a A de Mod-R, escrivim T(A) = A⊗RB. Llavors T és un functor exacte dret de Mod-R en la categoria dels grups abelians Ab (en el cas de què R sigui commutatiu, és un functor exacte dret de Mod-R en Mod-R), i els seus functors derivats esquerres LnT estan definits. Escrivim: és a dir, prenem una resolució projectiva
llavors eliminem el terme A i apliquem tensors a la resolució projectiva amb B, i obtenim el complex (notem que A⊗RB no apareix i l'última fletxa és simplement l'aplicació nul·la) i prenem l'homologia d'aquest complex. Successió espectralFixem una categoria abeliana, com per exemple la categoria de mòduls sobre un anell. Una successió espectral és una elecció d'un enter no-negatiu r0 i d'una col·lecció de tres successions:
 Una successió espectral doble conté molta informació que cal tenir en compte, però existeix una tècnica de visualització que fa que l'estructura de la successió espectral sigui més evident. Tenim tres índexs, r, p i q. Per a cada r, imaginem que tenim un full de paper de dibuix. Sobre aquest full, prenem p que sigui la direcció horitzontal i q que sigui la direcció vertical. A cada punt de la quadrícula tenim l'objecte . És força freqüent que n = p + q sigui un altre índex natural de la successió espectral. L'índex n recorre cada full diagonalment de nord-oest a sud-est. En el cas homològic, les diferencials tenen bi-grau (−r, r − 1), de tal manera que decrementen n en 1. En el cas cohomològic, n s'incrementa en 1. Quan r és zero, la diferencial mou els objectes un espai cap avall o cap amunt. Això és similar a la diferencial d'un complex de cadenes. Quan r és 1, la diferencial mou els objectes un espai cap a l'esquerra o cap a la dreta. Quan r és 2, la diferencial mou els objectes com un cavall en el joc dels escacs. Per a r més gran, la diferencial actua com un moviment generalitzat del cavall. Functor derivatSuposem que tenim un functor exacte esquerre covariant F : A → B entre dues categories abelianes A i B. Si 0 → A → B → C → 0 és una successió exacta curta de A, llavors aplicant F obtenim la successió exacta 0 → F(A) → F(B) → F(C), i hom es podria preguntar com es podria continuar aquesta successió cap a la dreta per tal de formar una successió exacta llarga. Resulta que, sota certes condicions, existeix una manera canònica d'aconseguir-ho, donada pels functors derivats drets de F. Per a tot i≥1, existeix un functor RiF: A → B, i la successió anterior continua així: 0 → F(A) → F(B) → F(C) → R¹F(A) → R¹F(B) → R¹F(C) → R²F(A) → R²F(B) → .... D'aquí podem veure que F és un functor exacte si i només si R¹F = 0; és a dir, els functors derivats drets de F proporcionen una mesura que quant "li falta" a F per ser exacte. FunctorialitatUna funció contínua d'espais topològics proporciona un homomorfisme entre els seus n-sims grups d'homologia per a tot n. Aquest resultat bàsic de topologia algebraica permet trobar una explicació natural a certes propietats dels complexos de cadenes. Com que és freqüent estudiar diversos espais topològics de manera simultània, en àlgebra homològica hom es veu sovint dirigit a considerar simultàniament diversos complexos de cadenes. Un morfisme entre dos complexos de cadenes, , és una família d'homomorfismes de grups abelians Fn:Cn → Dn que commuten amb les diferencials, en el sentit de què Fn -1 • dnC = dnD • Fn per a tot n. Un morfisme de complexos de cadenes indueix un morfisme dels seus grups d'homologia, consistent en els homomorfismes Hn(F): Hn(C) → Hn(D) per a tot n. Hom diu que un morfisme F és un quasi-isomorfisme si indueix un isomorfisme en la n-sima homologia per a tot n. En àlgebra i geometria, moltes construccions de cadenes de complexos que hi apareixen, incloent-hi l'holomogia singular, tenen la següent propietat de functorialitat: si dos objectes X i Y estan connectats per una aplicació f, llavors els complexos de cadenes associats estan connectats per un morfisme F = C(f) de en , i addicionalment, la composició g • f d'aplicacions f: X → Y i g: Y → Z indueix el morfisme C(g • f) de en que coincideix amb la composició C(g) • C(f). Una conseqüència d'això és que els grups d'homologia són també functorials, de tal manera que els morfismes entre objectes algebraics o topològics proporcionen aplicacions entre les seves homologies. La següent definició sorgeix d'una situació típica en àlgebra i topologia. Hom diu que un triplet consistent en tres complexos de cadenes i dos morfismes entre ells, , és un triplet exacte o una successió exacta curta de complexos, escrit si per a qualsevol n, la successió és una successió exacta curta de grups abelians. Per definició, això significa que fn és una funció injectiva, gn és una funció exhaustiva, i Im fn = Ker gn. Un dels teoremes més bàsics en àlgebra homològica, anomenat lema zig-zag, afirma que, en aquest cas, existeix una successió exacta llarga en homologia
on els grups d'homolohia de L, M, i N se segueixen cíclicament l'un a l'altre, i δn són uns certs homomorfismes determinats per f i g, anomenats els homomorfismes connectors. Aspectes fundacionalsDiversos autors han definit teories de cohomologia per a molts objectes diferents, com espais topològics, feixos, grups, anells, àlgebres de Lie i C*-àlgebres. L'estudi de la geometria algebraica moderna seria impensable sense la cohomologia de feixos. La noció de successió exacta és fonamental en àlgebra homològica, ja que es poden construir successions exactes per tal de realitzar càlculs efectius. Una eina clàssica en àlgebra homològica és el functor derivat; els exemples més bàsics són els functors Ext i Tor. Donat que s'estaven estudiant diferents aplicacions, era natural intentar abstreure tots aquests conceptes sota una base uniforme. Hi va haver diversos intents de fer aquesta feina d'abstracció. A continuació es presenta una història aproximada:
La punta de llaça computacional per excel·lència és la successió espectral; és essencial en els enfocaments de Cartan-Eilenberg i Tohoku, per exemple, per tal de computar els functors derivats d'una composició de dos functors. Les successions espectrals són menys essencials en l'enfocament de categoria derivada, però encara juga un rol important quan és necessari realitzar càlculs efectius. Existeixen intents en teories 'no-commutatives', que amplien la primera cohomologia com a torsors, importants en cohomologia de Galois. Referències
Bibliografia
|