順序回路

順序回路（じゅんじょかいろ、sequential circuit）とは、デジタル回路のうち外部からの入力信号と記憶されている内部状態（記憶回路）との組み合わせによって出力状態が決定されるもの。

最も単純な順序回路としてはラッチやフリップフロップがある。より大きなものとしてはレジスタやカウンタなどがあり^[1]、CPUも非常に大規模な順序回路といえる^[2]。

順序回路は、クロックパルスのタイミングのみで動作し出力が確定する同期式順序回路と、クロックパルス入力を持たず入力信号のタイミングに依存して出力が確定する非同期式順序回路に分類できる^[3]。

組み合わせ回路は入力信号に対して出力が一意に決定されるが、順序回路ではその内部で記憶されている状態（内部状態）と入力信号の状態によって次の出力状態が決定される。つまり、過去の入力信号変化が同じであってもある時点の内部状態が異なっていれば異なる出力状態になる。

順序回路の内部状態はフリップフロップやラッチで構成され、クロックパルスのタイミング（立ち上がり^{[注釈 1]}または立ち下がり^{[注釈 2]}）で状態が確定する同期式順序回路と、入力信号のタイミングに依存して状態が確定する非同期式順序回路に大別される。同期式順序回路ではクロックパルスごとに出力が確定するのでクロックパルスの周期よりも短い信号処理出力はできないが、内部の過渡的な遅延の影響を排除することが可能である。非同期式順序回路では処理速度は入力信号の変化速度に依存するが、内部の過渡的な遅延の影響が組み合わせ回路部や記憶回路部に発生するため、ハザードなどによる意図しない誤動作が発生しやすい^[4]。

最も基本となる順序回路は、同期式順序回路としてはフリップフロップ、非同期式順序回路としてはラッチがある。ただし、これらを一括してフリップフロップと呼ぶこともある^[5]、前者を同期式フリップフロップ、後者を非同期式フリップフロップと呼ぶ例もある^{[6][注釈 3]}。

なお、順序回路はオートマトン、状態機械、順序機械といった、

• 外部からの情報を入力
• 内部に状態を保持
• 外部からの情報と内部の状態から次の内部状態が決定
• 外部に情報を出力

というシステムを実現する方法の一つである^[7][8]。

順序回路の形式的な表現方法として、入出力や状態、遷移関数を以下のように表現する。

• X : 入力集合 (input set)
• Q : 状態集合 (state set)
• Z : 出力集合 (output set)
• δ : X × Q → Q 状態遷移関数 (state transition function)
• ω : 出力関数 (output function)

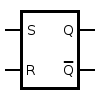
としたとき、順序回路は(X,Q,Z,δ,ω)の組として定義される。

ここで、出力関数ωをどのような形にするかで2つの形式に分かれる。

• ミーリ型(Mealy type) ： ω : X × Q → Z
• ムーア型(Moore type) ： ω : Q → Z

ムーア型では内部状態のみが出力に依存する関数となるが、ミーリ型とムーア型の本質的な違いはなく相互に変換可能である^[9][10]。

これらの組で表される順序回路の動作は状態遷移表や状態遷移図として表すことができる^[11]。

最も単純な順序回路の一つである RSラッチ(Reset/Set Latch)^{[注釈 4]}の例を示す。RSラッチでは、2つの入力 R、S に対して1つの出力Z（シンボル図におけるQ出力を指す^{[注釈 5]}）が決まる。Rを1にしたときには出力が0になり、Sを1にしたときには出力が1になる（ただし入力が同時になることは禁止する）。このとき、このような順序回路は

• X : R,S （R,S は 0 または 1。ただし同時に1になることは禁止）
• Q : Q₀ または Q₁ （ただし、Q₀=0、Q₁=1）
• Z : 0 または 1
• δ : 状態遷移表または状態遷移図を参照
• ω : 1 × Q → Z （実質的にはQをそのまま出力する）

と表現できる。

まず、RSラッチの状態遷移表を示す。なお、RSラッチでは(R,S)=(1,1)となる状態を禁止しているので表中では「-」（不定）としている^{[注釈 6]}。

RS ラッチの状態遷移表

	入力 RS
状態 Q	00	01	10	11
Q0 (=0)	Q0	Q1	Q0	-
Q1 (=1)	Q1	Q1	Q0	-

次に、ミーリ型およびムーア型の状態遷移図の例を示す。

ミーリ型において、節点には内部の状態、○○/●は入力条件が○○のときの出力が●に変化、矢印は条件が成立したときの遷移方向を表す。つまり、形式的表現における X=(R,S)、Z=0 or 1 を図中では RS/Z と表現し、それぞれに 1 または 0 が入る。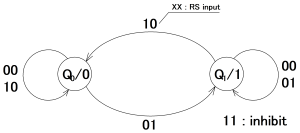

ムーア型では、節点には内部の状態と外部出力をまとめて○/○（内部状態/外部出力）と記し、矢印は入力条件○○が成立したときの遷移方向を表す。なお、RSラッチでは、内部状態Qと出力Zは同じなので、本例では Q₀/0、Q₁/1 という節点はあるが、Q₁/0、Q₀/1 という節点は無い。

同期式順序回路はクロックパルス専用の入力端子を持ち、クロックパルスが変化した時点（エッジ）の入力および内部状態に対して出力状態が変化する。これに対し、非同期式順序回路は入力状態が変化した時点の入力および内部状態に対して出力状態が変化する^[12]。 図.7 では、RSラッチとRSフリップフロップの動作の違いを示す。両方に同じR、S信号を入力したときのそれぞれの出力Q_a、Q_bである。ラッチではR、S信号が変化した時点でQ_aが変化しているが、フリップフロップではクロックパルスの立ち上がり時点のR、S信号の状態によってQ_bが変化する。（なお、初期状態はQ_a、Q_bとも1としている）

なお、複数の順序回路を用いて所定の機能を有する順序回路を生成する場合、個別の同期式順序回路を用いても同期式順序回路にはならないことがある。例えば、図.8 はリプルカウンタ（非同期式カウンタ）であり（同期式である）フリップフロップだけを用いて構成できるが同期式順序回路ではない。接続されるフリップフロップが共通するクロックパルスを入力した構成ではなく前段回路の出力が次段のクロックパルスとして使われるためである^[13][14][15]。

フリップフロップおよびラッチは1ビットの2つの状態（0または1）を記憶する最小の順序回路である^[16]。このような回路として、RSフリップフロップ/RSラッチ、Dフリップフロップ/Dラッチ、JKフリップフロップ、Tフリップフロップがある。下表に回路シンボルおよび状態遷移表を示す。

基本となる順序回路

回路タイプ	フリップフロップ	ラッチ	状態遷移表
RS			入力 RS 状態 Q 00 01 10 11 Q0 (=0) Q0 Q1 Q0 - Q1 (=1) Q1 Q1 Q0 - フリップフロップはクロックパルスのエッジでのみ有効
D			入力 D 状態 Q 0 1 Q0 (=0) Q0 Q1 Q1 (=1) Q0 Q1 フリップフロップはクロックパルスのエッジでのみ有効 ラッチはE (Enable)端子が1のときに有効[注釈 7]
JK		-	入力 JK 状態 Q 00 01 10 11 Q0 (=0) Q0 Q0 Q1 Q1 Q1 (=1) Q1 Q0 Q1 Q0 クロックパルスのエッジでのみ有効
T		-	入力 T,CK 状態 Q 0,↑ 1,↑ Q0 (=0) Q0 Q1 Q1 (=1) Q1 Q0 T=1かつクロックパルスの立ち上がりエッジでのみ状態が反転する

順序回路を組み合わせることにより様々な機能を持つ応用回路が実現でき、CPUもその一つである。ここでは基本機能であるレジスタとカウンタを例示する。

• 
  図.9 Dラッチを使用した4bit非同期式レジスタ (a) とDフリップフロップを使用した4bit同期式レジスタ (b)
• 
  図.10 JKフリップフロップを使用した4bit非同期式カウンタ (a) と4bit同期式カウンタ (b)

• 高木直史『論理回路』 9巻、昭晃堂〈New Text 電子情報系シリーズ〉、1997年4月。ISBN 4-7856-2150-8。 

• 赤堀寛、速水治夫『基礎から学べる論理回路』森北出版、2002年9月。ISBN 978-4-627-82761-5。 

• 浅川毅『論理回路の設計』コロナ社、2007年4月。ISBN 978-4-339-00788-6。 

• 南谷崇『論理回路の基礎』サイエンス社、2009年4月。ISBN 978-4-7819-1227-1。 

• 松下俊介『基礎からわかる論理回路』（第2版）森北出版、2021年7月。ISBN 978-4-627-82842-1。 

• 志村正道『電子回路 II [ディジタル編]』昭晃堂、1982年7月。ISBN 4-7856-1073-5。 

• 片方善治、生沼徳二、木下英実『半導体IC論理回路』 8巻、日刊工業新聞社〈電子回路設計シリーズ〉、1969年1月。 

• ディジタル回路
• 論理回路

• 論理回路基礎（UTokyo OpenCourseWare）