カーネル (英 : kernel )は、統計学において複数の異なる意味に用いられる語である。
統計学、特にベイズ統計学 において、ある確率密度関数 または確率質量関数 のカーネル とは、確率密度関数や確率質量関数の、ドメイン内のいかなる変数の関数でもないすべての因子が省略されるような形式である[要出典 。そのような因子は、それらの確率密度関数や確率質量関数のパラメーター の関数であってもよい。これらの因子は、確率分布 の正規化係数 の一部をなし、またそれらは多くの場合不要である。
例えば、擬似乱数サンプリング では、ほとんどのサンプリングアルゴリズムは正規化係数を無視する。さらに、共役事前確率分布 のベイズ分析では、計算途中において正規化係数は一般に無視され、カーネルのみが考慮される。最終的に、カーネルの形式が調査され、もしそれが既知の分布に一致すれば、正規化係数は復元されることができる。そうでなければ、正規化係数は不要かもしれない(例えば、その分布はサンプリングに用いられるだけであれば不要である)。多くの分布において、カーネルは閉形式で書くことができるが、正規化定数はそうではない。
一つの例は、正規分布 である。正規分布の確率密度関数 は
p
(
x
∣
μ
,
σ
2
)
=
1
2
π
σ
2
exp
(
−
(
x
−
μ
)
2
2
σ
2
)
{\displaystyle p(x\mid \mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}
であり、対応するカーネルは
p
(
x
∣
μ
,
σ
2
)
∝
exp
(
−
(
x
−
μ
)
2
2
σ
2
)
{\displaystyle p(x\mid \mu ,\sigma ^{2})\propto \exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}
である。
指数関数の前にある因子は、
σ
2
{\displaystyle \sigma ^{2}}
x
{\displaystyle x}
再生核ヒルベルト空間 (RKHS) のカーネルが、カーネル法 として知られる一連の手法において、implicit spaceのデータに対し、クラス識別 、回帰分析 、クラスター分析 などを実行するのに用いられる。この用法は特に機械学習 においてよく見られる。特にパラメーターに対して線形なクラスのモデルを用いる多くの機械学習手法を非線形化するために用いることができる。
RKHSを用いる機械学習手法で扱われる「カーネル」とは、対称性、正定値性(任意の有限個の入力空間の元に対して、グラム行列が半正定値)をともに満たす二変数関数のこと(総称)であり、ノンパラメトリック統計でカーネルと呼ばれるものとは一般に異なる。代表的なものにガウシアンカーネルがある。
ノンパラメトリック手法 において、カーネル とは、ノンパラメトリックな推定手法に用いられる重み付け関数のことである。カーネルは、確率変数 の確率密度関数 を推定するためのカーネル密度推定 や、確率変数の条件付き期待値 を推定するカーネル回帰 に用いられる。カーネルは時系列分析 においては窓関数 という名称で、ピリオドグラム によってスペクトル密度 を推定するのに用いられる。その他の利用法としては、点過程 の時間可変な強度の推定にも用いられる。そこでは窓関数(カーネル)は、時系列データとともに畳み込まれる。
ノンパラメトリックな推定を実行する際はふつう、(カーネル関数に加えて)カーネルの幅も指定されなければならない。
カーネルとは、非負実数値 可積分 関数 K であって、次の2つの条件を満たすもののことである。
∫
−
∞
+
∞
K
(
u
)
d
u
=
1
;
{\displaystyle \int _{-\infty }^{+\infty }K(u)\,du=1\,;}
K
(
−
u
)
=
K
(
u
)
for all values of
u
.
{\displaystyle K(-u)=K(u){\mbox{ for all values of }}u\,.}
一つめの要件は、カーネル密度推定の結果が確率密度関数 となることを担保するものである。
二つめの要件は、対応する分布の平均が、利用されたサンプルの平均に等しくなることを担保するものである。
もし K がカーネルであれば、λ > 0 に対して K *(u ) = λK (λu ) で定義される K * もカーネルとなる。この性質は、データに適したスケールを選択するために用いることができる。
いくつかの種類のカーネル関数がよく用いられる。たとえば一様、三角、Epanechnikov[ 1] [ 2] [ 3]
下の表において、1 {…} は指示関数 である。
カーネル関数, K (u )
∫
u
2
K
(
u
)
d
u
{\displaystyle \textstyle \int u^{2}K(u)du}
∫
K
(
u
)
2
d
u
{\displaystyle \textstyle \int K(u)^{2}du}
Epanechnikov カーネルに対する相対効率
一様
K
(
u
)
=
1
2
1
{
|
u
|
≤
1
}
{\displaystyle K(u)={\frac {1}{2}}\,\mathbf {1} _{\{|u|\leq 1\}}}
1
3
{\displaystyle {\frac {1}{3}}}
1
2
{\displaystyle {\frac {1}{2}}}
1.076
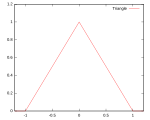
三角
K
(
u
)
=
(
1
−
|
u
|
)
1
{
|
u
|
≤
1
}
{\displaystyle K(u)=(1-|u|)\,\mathbf {1} _{\{|u|\leq 1\}}}
1
6
{\displaystyle {\frac {1}{6}}}
2
3
{\displaystyle {\frac {2}{3}}}
1.014
Epanechnikov
K
(
u
)
=
3
4
(
1
−
u
2
)
1
{
|
u
|
≤
1
}
{\displaystyle K(u)={\frac {3}{4}}(1-u^{2})\,\mathbf {1} _{\{|u|\leq 1\}}}
1
5
{\displaystyle {\frac {1}{5}}}
3
5
{\displaystyle {\frac {3}{5}}}
1.000
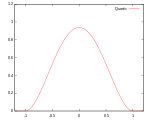
Quartic
K
(
u
)
=
15
16
(
1
−
u
2
)
2
1
{
|
u
|
≤
1
}
{\displaystyle K(u)={\frac {15}{16}}(1-u^{2})^{2}\,\mathbf {1} _{\{|u|\leq 1\}}}
1
7
{\displaystyle {\frac {1}{7}}}
5
7
{\displaystyle {\frac {5}{7}}}
1.006
Triweight
K
(
u
)
=
35
32
(
1
−
u
2
)
3
1
{
|
u
|
≤
1
}
{\displaystyle K(u)={\frac {35}{32}}(1-u^{2})^{3}\,\mathbf {1} _{\{|u|\leq 1\}}}
1
9
{\displaystyle {\frac {1}{9}}}
350
429
{\displaystyle {\frac {350}{429}}}
1.013
Tricube
K
(
u
)
=
70
81
(
1
−
|
u
|
3
)
3
1
{
|
u
|
≤
1
}
{\displaystyle K(u)={\frac {70}{81}}(1-{\left|u\right|}^{3})^{3}\,\mathbf {1} _{\{|u|\leq 1\}}}
35
243
{\displaystyle {\frac {35}{243}}}
175
247
{\displaystyle {\frac {175}{247}}}
1.002
ガウシアン
K
(
u
)
=
1
2
π
exp
(
−
1
2
u
2
)
{\displaystyle K(u)={\frac {1}{\sqrt {2\pi }}}\exp \left(-{\frac {1}{2}}u^{2}\right)}
1
{\displaystyle 1\,}
1
2
π
{\displaystyle {\frac {1}{2{\sqrt {\pi }}}}}
1.051
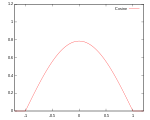
コサイン
K
(
u
)
=
π
4
cos
(
π
2
u
)
1
{
|
u
|
≤
1
}
{\displaystyle K(u)={\frac {\pi }{4}}\cos \left({\frac {\pi }{2}}u\right)\mathbf {1} _{\{|u|\leq 1\}}}
1
−
8
π
2
{\displaystyle 1-{\frac {8}{\pi ^{2}}}}
π
2
16
{\displaystyle {\frac {\pi ^{2}}{16}}}
1.0005
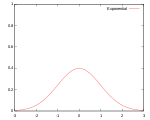
ロジスティック
K
(
u
)
=
1
e
u
+
2
+
e
−
u
{\displaystyle K(u)={\frac {1}{e^{u}+2+e^{-u}}}}
π
2
3
{\displaystyle {\frac {\pi ^{2}}{3}}}
1
6
{\displaystyle {\frac {1}{6}}}
1.127
Silverman カーネル[ 4]
K
(
u
)
=
1
2
exp
(
−
|
u
|
2
)
sin
(
|
u
|
2
+
π
4
)
{\displaystyle K(u)={\frac {1}{2}}\exp \left(-{\frac {|u|}{\sqrt {2}}}\right)\sin \left({\frac {|u|}{\sqrt {2}}}+{\frac {\pi }{4}}\right)}
0
{\displaystyle 0}
3
2
16
{\displaystyle {\frac {3{\sqrt {2}}}{16}}}
適用できない
効率性は
(
∫
u
2
K
(
u
)
d
u
)
1
/
2
∫
K
(
u
)
2
d
u
{\displaystyle \left(\int u^{2}K(u)du\right)^{1/2}\int K(u)^{2}du}
^ Named for Epanechnikov, V. A. (1969). “Non-Parametric Estimation of a Multivariate Probability Density”. Theory Probab. Appl. 14 (1): 153–158. doi :10.1137/1114019 .
^ Altman, N. S. (1992). “An introduction to kernel and nearest
neighbor nonparametric regression”. The American Statistician 46 (3): 175–185. doi :10.1080/00031305.1992.10475879 . ^ Cleveland, W. S. & Devlin, S. J. (1988). “Locally weighted regression: An approach to regression analysis by local fitting”. Journal of the American Statistical Association 83 : 596–610. doi :10.1080/01621459.1988.10478639 . ^ Silverman, B. W. (1986). Density Estimation for Statistics and Data Analysis . Chapman and Hall, London
Li, Qi; Racine, Jeffrey S. (2007). Nonparametric Econometrics: Theory and Practice . Princeton University Press. ISBN 0-691-12161-3 Comaniciu, D; Meer, P (2002). “Mean shift: A robust approach toward feature space analysis”. IEEE Transactions on Pattern Analysis and Machine Intelligence 24 (5): 603–619. doi :10.1109/34.1000236 . CiteSeerx : 10.1.1.76.8968 .