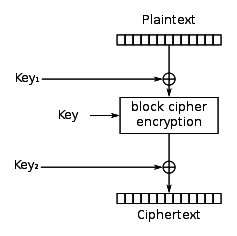
DES-X

In cryptography, DES-X (or DESX) is a variant on the DES (Data Encryption Standard) symmetric-key block cipher intended to increase the complexity of a brute-force attack. The technique used to increase the complexity is called key whitening.

The original DES algorithm was specified in 1976 with a 56-bit key size: 2⁵⁶ possibilities for the key. There was criticism that an exhaustive search might be within the capabilities of large governments, particularly the United States' National Security Agency (NSA). One scheme to increase the key size of DES without substantially altering the algorithm was DES-X, proposed by Ron Rivest in May 1984.

The algorithm has been included in RSA Security's BSAFE cryptographic library since the late 1980s.

DES-X augments DES by XORing an extra 64 bits of key (K₁) to the plaintext before applying DES, and then XORing another 64 bits of key (K₂) after the encryption:

${\displaystyle {\mbox{DES-X}}(M)=K_{2}\oplus {\mbox{DES}}_{K}(M\oplus K_{1})}$

The key size is thereby increased to 56 + (2 × 64) = 184 bits.

However, the effective key size (security) is only increased to 56+64−1−lb(M) = 119 − lb(M) = ~119 bits, where M is the number of chosen plaintext/ciphertext pairs the adversary can obtain, and lb denotes the binary logarithm. Moreover, effective key size drops to 88 bits given 2^32.5 known plaintext and using advanced slide attack.

DES-X also increases the strength of DES against differential cryptanalysis and linear cryptanalysis, although the improvement is much smaller than in the case of brute force attacks. It is estimated that differential cryptanalysis would require 2⁶¹ chosen plaintexts (vs. 2⁴⁷ for DES), while linear cryptanalysis would require 2⁶⁰ known plaintexts (vs. 2⁴³ for DES or 2⁶¹ for DES with independent subkeys.^[1]) Note that with 2⁶⁴ plaintexts (known or chosen being the same in this case), DES (or indeed any other block cipher with a 64 bit block size) is totally broken as the whole cipher's codebook becomes available.

Although the differential and linear attacks, currently best attack on DES-X is a known-plaintext slide attack discovered by Biryukov-Wagner ^[2] which has complexity of 2^32.5 known plaintexts and 2^87.5 time of analysis. Moreover the attack is easily converted into a ciphertext-only attack with the same data complexity and 2⁹⁵ offline time complexity.

• G-DES
• Meet-in-the-middle attack
• Triple DES
• Xor–encrypt–xor

• Kilian, Joe; Rogaway, Phillip (1996). "How to Protect DES Against Exhaustive Key Search". Advances in Cryptology — CRYPTO '96. Lecture Notes in Computer Science. Vol. 1109. pp. 252–267. doi:10.1007/3-540-68697-5_20. ISBN 978-3-540-61512-5.
• P. Rogaway, The security of DESX (PDF), CryptoBytes 2(2) (Summer 1996).

• RSA FAQ Entry