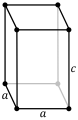
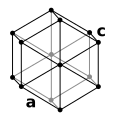
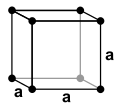
Krystalová mřížka

Je navrženo začlenění celého obsahu článku Bravaisova mřížka do tohoto článku.

Odtamtud sem pak má vést přesměrování. K návrhu se můžete vyjádřit v diskusi.

Krystalová mřížka je množina určitých myšlených abstraktních bodů, pomocí nichž se popisuje struktura krystalu neboli vzájemná poloha částic v krystalu.

Krystalová mřížka znázorňuje jednotlivé částice (atomy, ionty, molekuly) bez ohledu na jejich velikost jako body a ty se nazývají uzly. Dva libovolné uzly v krystalové mřížce jsou spojeny přímkou, která se nazývá mřížkový vektor. Způsob uspořádání uzlů se nazývá krystalická struktura a je to vlastně její idealizovaný geometrický obraz nebo model.

V každé krystalové mřížce můžeme určit rovnoběžnostěn, jehož uspořádání částic se pravidelně opakuje v celé mřížce. Tento rovnoběžnostěn se nazývá elementární buňka nebo také základní buňka. Každá elementární buňka je definována šesti mřížkovými parametry. Jsou to délky jejich stran (mřížkové vektory) a, b, c a úhly α, β, γ, které tyto strany svírají.

V přírodě není možné dosáhnout ideální krystalové mřížky, jejíž struktura by byla zcela pravidelná a bez jakýchkoliv krystalových poruch.

Související informace naleznete také v článku Krystalografická soustava.

Krystalové mřížky se od sebe odlišují tvarem elementární buňky, jejími rozměry, polohami částic a velikostmi úhlů. Podle těchto mřížkových parametrů (vektorů a, b, c a úhlů mezi nimi α, β, γ) se krystalové mřížky rozdělují na 7 základních typů:

• jednoklonná (monoklinická) – a₀ ≠ b₀ ≠ c₀, α = γ, β > 90°
• trojklonná (triklinická) – a₀ ≠ b₀ ≠ c₀, α ≠ β ≠ γ ≠ 90°
• kosočtverečná (ortorombická) – a₀ ≠ b₀ ≠ c₀, α = β = γ = 90°
• čtverečná (tetragonální) – a₀ = b₀ ≠ c₀, α = β = γ = 90°
• šesterečná (hexagonální) – a₀ = b₀ ≠ c₀ resp. a₁ = a₂ = a₃ ≠ c₀, α = β = 90°, γ = 120°
• klencová (trigonální) – a₀ = b₀ = c₀, (α = β = γ) ≠ 90°
• krychlová (kubická) – a = b = c, α = β = γ = 90°

• 
  Jednoklonná
• 
  Trojklonná
• 
  Kosočtverečná
• 
  Čtverečná
• 
  Šesterečná
• 
  Klencová
• 
  Krychlová

K popisu krystalových struktur se běžně používají také Bravaisovy mřížky, které mohou být jednorozměrné (lineární), dvojrozměrné (rovinné) a trojrozměrné (prostorové).

Krystalové struktury minerálů popisují trojrozměrné Bravaisovy mřížky, které se podle typu jejich elementární buňky rozdělují na primitivní a centrované.

Existuje pouze 14 jedinečných možností, jak v prostoru poskládat elementární buňky a tím vznikne14 prostorových Bravaisových mřížek. Elementární buňka musí splňovat tato Bravaisova pravidla:

1. Počet pravých úhlů v základní buňce musí být maximální.
2. Symetrie základní buňky musí být shodná se symetrií celé mřížky.
3. Při dodržení předchozích podmínek musí být objem základní buňky minimální.
4. V případě, kdy symetrie nemůže rozhodnout, vybírá se základní buňka, tak aby její hrany byly co nejkratší.

Stejně jako u krystalové mřížky jsou základní vektory (a, b, c) definovány hranami elementární buňky a jejich délky jsou základní periody mřížky. Společně se třemi úhly (α, β, γ), které základní vektory svírají, tvoří těchto šest hodnot mřížkové parametry.

Související informace naleznete také v článku Krystalová porucha.

Podobně jako u krystalu, tak ani u krystalové mřížky není možné dosáhnout struktury, která by byla zcela pravidelná a bez jakýchkoliv poruch. Plně zaplněná krystalová mřížka je ideální stav, ve skutečném světě mají krystaly poruchy mřížky, které lze rozdělit na:

• Bodové poruchy
  • substituční atom – příměs atomu jiného prvku do krystalového materiálu (např. v polovodičích)
  • intersticiální atom – cizí atom v meziuzlové poloze (tzn. atom vmísen mezi dvě patra krystalové struktury)
  • vakance – chybí částice v uzlové poloze
  • Frenkelova porucha – kombinace poruchy intersticiálního atomu a vakance (atom se dostal z řádné do intersticiální polohy)
  • Schotkyho porucha – 2 vakance (chybí aniont a kationt)
• Lineární poruchy (dislokace)
  • hranová – chybí souvislá část atomů v jedné vrstvě mřížky, následná deformace ostatních vrstev směrem k vzniklé mezeře
  • šroubová – posun celé struktury o půlotáčku
  • disklinace – stočení mřížkového vektoru – deformace vrstev tak, že vzniknou nové osy symetrie
• Plošné
  • mozaika – pravidelné bloky krystalové mřížky vázané na sebe nepravidelně (jako polykrystaly ale bez plynných částí)
  • hranice zrn

• Krystal
• Krystalická struktura
• Krystalografická soustava
• Elementární buňka
• Krystalová porucha
• Krystalografie

V tomto článku byly použity překlady textů z článků Bravais lattice na anglické Wikipedii a Bravais-Gitter na německé Wikipedii.

• Obrázky, zvuky či videa k tématu krystalová mřížka na Wikimedia Commons