|
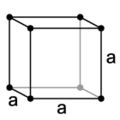
| Kubická soustava |
|---|
 | | Metrika | a=b=c, α=β=γ=90° |
|---|
| Bravaisovy mřížky | P, I, F |
|---|
| Souměrnost | střed souměrnosti, tři čtyřnásobné osy souměrnosti, čtyři trojnásobné osy, šest dvojnásobných os, devět rovin souměrnosti |
|---|
| Krystalové tvary | tetraedr, hexaedr, oktaedr, hexaoktaedr, tetragon-tir oktaedr, trigon-tri oktaedr, pentagon-tri oktaedr, tetrahexaedr, rombododekaéder, pentagondodekaedr, didokekaedr, hexatetradr, trigon-tri tetraedr, tetragon-tri tetraedr a pentagon-tri tetraedr |
|---|
Krychlová, kubická (nebo izometrická) krystalová soustava je jedna ze sedmi krystalových soustav. Je to soustava s nejvyšší symetrií, charakteristická je přítomnost čtyř trojnásobných os souměrnosti, dalších tělesové úhlopříčky. Možné prvky souměrnosti jsou: tři čtyřnásobné osy souměrnosti (symbol 4), čtyři trojnásobné osy (3), šest dvojnásobných os (2), maximálně devět rovin souměrnosti (m), střed souměrnosti (1) a jejich kombinace. Bravaisovy mřížky jsou zastoupené tři: primitivní (P) a prostorově centrovaná (I) a plošně centrovaná (F).
Typy mřížek
Výběr souřadnicové soustavy
Jako krystalografické osy lze vybrat libovolnou ze tří os souměrnosti (4, 4, nebo 2).
Krystalové tvary
V jednotlivých grupách jsou možné další tvary:
- m3m - hexaedr, rombododekaedr, tetrahexaedr, tetragon-tři oktaedr, trigon-tri oktaedr, hexaoktaedr
- m3 - hexaedr, rombododekaedr, pentasgonálny dodekaedr, oktaedr, tetragon-tri oktaedr, trigon-tri oktaedr, didodekaedr
- 432 - hexaedr, rombododekaedr, tetrahexaedr, oktaedr, tetragon-tri oktaedr, trigon-tri oktaedr, pentagon-tri oktaedr
- 43m - hexaedr, rombododekaedr, tetrahexaedr, tetraedr, trigon-tri tetraedr, tetragon-tri tetraedr, hexatetraedr
- 23 - hexaedr, rombododekaedr, pentagonální dodekaedr, tetraedr, trigon-tři tetraedr, tetragon-tri tetraedr, pentagon-tři tetraedr
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Kubická sústava na slovenské Wikipedii.
Externí odkazy
|