Share to: share facebook share twitter share wa share telegram print page

 

Швидкість світла

Швидкість світла
Сонячному світлу потрібно близько 8 хвилин і 17 секунд, щоб дістатись від Сонця до Землі.
Точна величина
метрів за секунду299792458
Наближені значення (до третього знака)
кілометрів за годину1080000000
астрономічних одиниць за день173[Прим. 1]
парсеків за рік0,307[Прим. 2]
Приблизний час польоту світла
Відстаньчас
один метр3,3 нс
з геостаціонарної орбіти до Землі119 мс
довжина екватора Землі134 мс
від Місяця до Землі1,3 с
від Сонця до Землі (1 а.о.)8,3 хв
один світловий рік1,0 рік
один парсек3,26 року
від найближчої зорі до Сонця (1,3 пк)4,2 року
від найближчої галактики до Землі70000 років
через Чумацький Шлях90000 років
від Галактика Андромеди до Землі2,5 млн років

Швидкість світла у вакуумі зазвичай позначається як c й дорівнює точно 299792458 м/с[3]. Відповідно до спеціальної теорії відносності Ейнштейна, c — це верхня межа швидкості, з якою можуть рухатись частинки або передаватись будь-який сигнал[4][5][6]. Швидкість світла в речовині менша за швидкість світла у вакуумі в n разів, де n — показник заломлення речовини.

Усі форми електромагнітного випромінювання у вакуумі поширюються зі швидкістю світла. Для багатьох практичних цілей світло та інші електромагнітні хвилі поширюються миттєво, але для великих відстаней і дуже чутливих вимірювань скінченність їхньої швидкості має помітний ефект. Світло зір приходить на Землю із запізненням в багато років, що дозволяє вивчати давнє минуле Всесвіту, спостерігаючи далекі об'єкти. Під час зв'язку з далекими космічними апаратами передача сигналу може тривати багато хвилин або навіть кілька годин. В обчислювальній техніці швидкість світла задає мінімально можливу затримку зв'язку. Запізнення прибуття світло сигналу може використовуватись для визначення відстаней об'єктів, — наприклад, в радарах або в системах GPS.

У 1676 році Оле Ремер вперше виміряв швидкість світла[en], вивчаючи видимий рух Іо, супутника Юпітера. Протягом наступних століть з'являлися точніші вимірювання. У статті[en], опублікованій у 1865 році, Джеймс Клерк Максвелл припустив, що світло є електромагнітною хвилею і, отже, поширюється зі швидкістю c[7]. У 1905 році Альберт Ейнштейн постулював, що швидкість світла c відносно будь-якої інерціальної системи відліку є сталою і не залежить від руху джерела світла[8]. З цього постулату він вивів теорію відносності, показавши таким чином, що параметр c важливий не тільки для світла та електромагнетизму.

Безмасові частинки та поля, такі як гравітаційні хвилі, також рухаються у вакуумі зі швидкістю c. Частинки з відмінною від нуля масою спокою можуть наближатись до швидкості c, але не в змозі досягти її. У спеціальній і загальній теоріях відносності c пов'язує простір і час, а також фігурує у відомому рівнянні еквівалентності маси та енергії E = mc2[9].

У деяких випадках може здаватися, що об'єкти або хвилі рухаються швидше за світло (наприклад, фазові швидкості хвиль, вигляд певних високошвидкісних астрономічних об'єктів, окремі квантові ефекти). Розширення Всесвіту на певній відстані від спостерігача[en] досягає швидкості світла.

Швидкість, з якою світло поширюється крізь прозорі матеріали, такі як скло або повітря, менша за c. Аналогічно, швидкість електромагнітних хвиль у дротяних кабелях менша за c. Співвідношення між c та швидкістю v, з якою світло поширюється в матеріалі, називається показником заломлення n матеріалу (n = c/v) Наприклад, для видимого світла показник заломлення скла зазвичай становить близько 1,5, тобто світло в склі поширюється зі швидкістю c/1,5 ≈ 200 000 км/с. Показник заломлення повітря для видимого світла становить близько 1,0003, тому швидкість світла в повітрі приблизно на 90 км/с менша, ніж c.

Позначення

Швидкість світла у вакуумі зазвичай позначають малою літерою c, від «константа» або від латинського celeritas (що значить «швидкість, стрімкість»). У 1856 році Вільгельм Вебер і Рудольф Кольрауш використали c для іншої сталої, яка, як було показано пізніше, дорівнює √2 швидкостям світла. Історично як альтернативне позначення для швидкості світла вживався символ V, що його увів Джеймс Клерк Максвелл 1865 року. В 1894 році Пауль Друде[en] ще раз означив c у сучасному значенні. Альберт Ейнштейн використовував V у своїх оригінальних німецькомовних статтях зі спеціальної теорії відносності в 1905 році, одначе 1907 року він перейшов на c, яке стало стандартним позначенням для швидкості світла[10][11].

Інколи c вживають для швидкості хвиль у будь-якій речовині, а c0 для швидкості світла у вакуумі[12]. Це позначення з індексом, схвалене в офіційній літературі системи SI[13], має таку саму форму, як відповідні електромагнітні константи: μ0 для магнітної сталої, ε0 для електричної сталої, Z0 для хвильового опору вакууму. Ця стаття використовує c виключно для швидкості світла у вакуумі.

З 1983 року константа c була визначена в Міжнародній системі одиниць рівною точно 299792458; це використовується для визначення метра як відстані, яку світло проходить у вакуумі рівно за 1⁄299792458 секунди. Таким чином, використовуючи значення c, а також точне вимірювання секунди, можна встановити стандарт для метра[14].

У галузях фізики, де c часто зустрічається, наприклад, у теорії відносності, зазвичай використовують природні системи одиниць, в яких c = 1[15][16].

Швидкість світла як фундаментальна фізична стала

Фундаментальна фізична стала швидкість світла в Міжнародній системі одиниць SI її визначено резолюцією 1 17-ї Генеральної конференції мір і ваг[17]:

c = 299 792 458 м/с.

Це єдина фізична стала в основних рівняннях електродинаміки. Вона не залежить від системи відліку, тобто однакова для будь-якого спостерігача незалежно від швидкості, з якою цей спостерігач рухається. Це твердження є основним постулатом теорії відносності Ейнштейна.

Відповідно до теорії відносності, ніяка інформація не може бути передана зі швидкістю, яка перевищувала б швидкість світла. Якщо це не так, то існуватиме така система відліку, в якій інформацію буде отримано раніше, ніж вона надіслана.

Оскільки швидкість світла — фундаментальна і незалежна від спостерігача величина, то її значення можна застосувати для побудови системи фізичних одиниць. Наприклад, можна обрати систему одиниць так, щоб швидкість світла в ній дорівнювала одиниці. Такі системи одиниць називають природними і їх застосовують у теоретичній фізиці. Проте природні системи дуже незручні на практиці. Тому, оскільки швидкість має розмірність довжини, поділеної на час, можна вважати її рівною певному значенню, близькому до експериментально виміряного з застосуванням традиційних одиниць довжини й часу — метра й секунди, а потім зафіксувати це значення. Таким чином швидкість світла отримала подане вище значення. Надалі вона не буде визначатись з експерименту. Її фіксоване значення тепер слугуватиме для дослідного визначення одиниць довжини.

Фундаментальна роль у фізиці

γ starts at 1 when v equals zero and stays nearly constant for small v's, then it sharply curves upwards and has a vertical asymptote, diverging to positive infinity as v approaches c.
Фактор Лоренца (Лоренц-фактор) γ як функція швидкості. Він зростає від 1 (для нульової швидкості) до нескінченності (із наближенням v до c).

Швидкість, із якою світлові хвилі поширюються у вакуумі, не залежить ні від руху джерела хвиль, ні від системи відліку спостерігача[Прим. 3]. Ейнштейн постулював таку інваріантність швидкості світла 1905 року[18]. Він дійшов цього висновку виходячи з теорії електромагнетизму Максвелла та відсутності доказів існування світлоносного ефіру[19]. Відтоді інваріантність швидкості світла незмінно підтверджується безліччю експериментів. Існує можливість перевірити експериментально лише те, що швидкість світла в «двосторонньому» експерименті (наприклад, від джерела до дзеркала і назад) є незалежною від системи відліку, оскільки неможливо виміряти швидкість світла в один бік (наприклад, від джерела до віддаленого приймача) без додаткових домовленостей щодо того, як синхронізувати годинники джерела та приймача. Однак, якщо застосувати для цього синхронізацію Ейнштейна, одностороння швидкість світла стає рівною двосторонній за визначенням[20][21]. Спеціальна теорія відносності досліджує наслідки цієї інваріантності с у припущенні, що закони фізики однакові в усіх інерційних системах відліку[22][23]. Одним із наслідків є те, що c — це та швидкість, з якою мають рухатись у вакуумі всі безмасові частинки та хвилі (зокрема, і світло).

Спеціальна теорія відносності має багато експериментально перевірених наслідків, які суперечать інтуїції[24]. Такі наслідки включають: еквівалентність маси та енергії (), скорочення довжини (скорочення об'єктів під час руху) [Прим. 4] та уповільнення часу (рухомий годинник іде повільніше). Коефіцієнт γ, на який скорочується довжина та уповільнюється час, відомий як фактор Лоренца (Лоренц-фактор) , де V — швидкість об'єкта. Для швидкостей набагато менших, ніж c (наприклад, для швидкостей, з якими ми маємо справу повсякдень) різниця між γ та 1 настільки мала, що нею можна знехтувати. У цьому випадку спеціальна теорія відносності добре апроксимується відносністю Галілея. Однак на релятивістських швидкостях різниця збільшується та наближається до нескінченності з наближенням V до с.

Об'єднання результатів спеціальної теорії відносності потребує виконання двох умов: (1) простір і час є єдиною структурою, відомою як простір-час (де c пов'язує одиниці вимірювання простору та часу), та (2) фізичні закони задовольняють вимогам особливої симетрії, яка має назву інваріантність Лоренца (Лоренц-інваріантність), формула якої містить параметр с[27]. Інваріантність Лоренца є майже універсальним припущенням сучасних фізичних теорій, таких як квантова електродинаміка, квантова хромодинаміка, стандартна модель фізики елементарних частинок і загальна теорія відносності. Отже, параметр с наявний повсюди в сучасній фізиці та з'являється в багатьох контекстах, які не мають стосунку власне до світла. Наприклад, загальна теорія відносності передбачає, що гравітація та гравітаційні хвилі розповсюджуються зі швидкістю c[28][29]. У неінерційних системах відліку (у гравітаційно викривленому просторі або в системах відліку, що рухаються з прискоренням), локальна швидкість світла також є постійною та дорівнює c, проте швидкість світла вздовж траєкторії скінченної довжини може відрізнятись від c залежно від того, як визначено простір і час[30].

Вважається, що фундаментальні константи, такі як c, мають однакове значення в усьому просторі-часі, тобто, вони не залежать від місця та не змінюються з часом. Однак, деякі теорії припускають, що швидкість світла може змінюватись із часом[31][32]. Наразі немає переконливих доказів таких змін, одначе вони надалі є предметом досліджень[33][34].

Крім того, вважається, що швидкість світла ізотропна, тобто не залежить він напрямку його поширення. Спостереження за випромінюванням ядерних енергетичних переходів як функції від орієнтації ядер у магнітному полі (експеримент Гугса — Древера[en]), а також обертових оптичних резонаторів (експеримент Майкельсона — Морлі), наклали жорсткі обмеження на можливість існування двосторонньої анізотропії[35][36].

Верхня межа швидкості

Згідно зі спеціальною теорією відносності, енергія об'єкту з масою спокою m та швидкістю v дорівнює γmc2, де γ — визначений вище фактор Лоренца. Коли v дорівнює нулю γ дорівнює одиниці, що призводить до відомої формули еквівалентності маси та енергії E = mc2. Оскільки фактор γ наближається до нескінченності із наближенням v до  c, прискорення масивного об'єкта до швидкості світла потребуватиме нескінченної енергії. Швидкість світла — це верхня межа швидкості для об'єктів із масою спокою. Це експериментально встановлено в багатьох тестах релятивістської енергії та імпульсу[37].

""
Подія A передує події B у червоній системі відліку (СВ), одночасна з B у зеленій СВ та відбувається після B у синій СВ.

Взагалі, інформація або енергія не може передаватися швидше, ніж c. Один з аргументів на користь цього випливає з контр-інтуітивного висновку спеціальної теорії відносності, відомого як відносність одночасності. Якщо просторова відстань між двома подіями А та В більша, ніж проміжок часу між ними помножений на c, то існують системи відліку, в яких А передує B, та інші, в яких B передує А, а також такі, в яких події А та B одночасні. В результаті, якщо об'єкт рухався б швидше ніж c відносно деякої інерційної системи відліку, то в іншій системі відліку він би подорожував назад у часі, та принцип причинності було б порушено. [Прим. 5][39]. У такій системі відліку «наслідок» можна було б спостерігати раніше його «першопричини». Таке порушення причинності ніколи не спостерігалося[21]. Воно також може призводити до парадоксів, таких як тахіонний антителефон[40].

Видимий надсвітловий рух

Докладніше: Надсвітловий рух

Бувають ситуації, коли може здатися, що речовина, енергія або сигнал поширюється з надсвітловою швидкістю, хоч насправді цього не відбувається.

При поширенні електромагнітних хвиль через середовище фазова швидкість іноді перевищує c (наприклад, для рентгенівського випромінювання при проходженні через більшість сортів скла[41]), але інформація передається не з фазовою, а з груповою швидкістю[42], яка залишається меншою за c.

Якщо лазерний промінь швидко проходить по віддаленому об'єкту, світлова пляма може рухатися швидше, ніж c. Однак рухомими фізичними об'єктами при цьому є тільки лазер і випромінюване ним світло, яке поширюється зі швидкістю c від лазера до різних положень плями, а сама пляма не переносить ані матерії, ані інформації. Так само тінь, спроєктовану на віддалений об'єкт, можна змусити рухатися швидше, ніж c[43]. У кожному з цих випадків жодна матерія, енергія чи інформація не рухаються швидше за світло[44].

Швидкість зміни відстані між двома об'єктами в системі відліку, відносно якої обидва рухаються (їх швидкість зближення), може перевищувати c. Однак при цьому швидкість будь-якого об'єкта в будь-якій інерціальній системі відліку залишається меншою за c[45] (наприклад, швидкість одного рухомого об'єкта в системі відліку, пов'язаній з іншим об'єктом, — це є проявом нелінійності додавання швидкостей в теорії відносності).

Певні квантові ефекти передаються миттєво і, отже, швидше, ніж c, наприклад, парадокс Ейнштейна-Подольського-Розена. Прикладом є сплутані квантові стани двох частинок. Поки жодна з частинок не спостерігається, вони існують як суперпозиція двох квантових станів. Коли ж вимірюється квантовий стан однієї частинки, квантовий стан іншої частинки визначається миттєво. Однак неможливо контролювати, який квантовий стан прийме перша частинка, коли її спостерігають, тому інформація не може бути передана таким чином[46][47].

Інший квантовий ефект, який передбачає виникнення швидкостей, вищих за швидкість світла, називається ефектом Гартмана: за певних умов час, необхідний віртуальній частинці для тунелювання через бар'єр, є сталим, незалежно від товщини бар'єру[48][49]. Це може призвести до того, що віртуальна частинка перетне бар'єр швидше за світло. Однак, знову ж таки, інформація не може бути передана за допомогою цього ефекту[50].

Експеримент 2011 року, який визначив, що нейтрино рухалися швидше за світло(інші мови), виявився результатом експериментальної помилки[51][52].

Так званий надсвітловий рух спостерігається у деяких астрономічних об'єктах[53], таких як релятивістські струмені радіогалактик і квазарів. Однак при цьому з надсвітловою швидкістю рухаються не самі струмені, а тільки освітлені ними ділянки інших об'єктів. Цей надсвітловий рух подібний надсвітловому руху кінця світлового променя, і так само нездатний передавати інформацію з надсвітловою швидкістю[54].

У моделях розширення Всесвіту більш далекі галактики віддаляються з більшою швидкістю. За межею, званою сферою Габбла, швидкість віддалення галактик від Землі стає більшою за швидкість світла[55]. Ці швидкості віддалення, визначені як збільшення власної відстані за космологічний час, не є швидкостями в релятивістському сенсі. Швидкість космологічного віддалення, вища за швидкість світла, є лише артефактом координат.

Поширення світла

У класичній фізиці світло описується як електромагнітна хвиля. З рівнянь Максвелла випливає, що швидкість, з якою електромагнітні хвилі поширюються у вакуумі, пов'язана електричною сталою ε0 і магнітною сталою μ0 формулою[56]

У сучасній квантовій фізиці електромагнітне поле описується квантовою електродинамікою. У цій теорії світло описується фундаментальними збудженнями (або квантами) електромагнітного поля, які називаються фотонами. Фотони є безмасовими частинками і тому, відповідно до спеціальної теорії відносності, рухаються зі швидкістю світла у вакуумі[57].

У середовищі

Заломлення світла

У середовищі швидкість світла, тобто швидкість розповсюдження електромагнітних хвиль, змінюється через процеси поляризації атомів і молекул речовини. Відношення швидкості світла в середовищі й у вакуумі називають абсолютним показником заломлення у цьому середовищі:

де cm — швидкість світла в середовищі.

Для електромагнітних хвиль із різною частотою показник заломлення різний. Це явище називається дисперсією світла. Розрізняють фазову швидкість світла, яка визначається показником заломлення, і групову швидкість.

Фазова швидкість світла характеризує зв'язок між довжиною хвилі й частотою. Вона визначається для необмежених у просторі плоских хвиль, які не можуть переносити інформацію. Фазова швидкість може перевищувати швидкість світла у вакуумі. При цьому принцип причинності не порушується.

Групова швидкість світла в середовищі характеризує процес розповсюдження хвильового пакета, яким може передаватися інформація. Групова швидкість завжди менша за швидкість світла у вакуумі, що задовольняє принцип причинності.

Практичне значення скінченності швидкості світла

Скінченність швидкості світла створює труднощі, коли накладає обмеження на швидкість зв'язку. З іншого боку, вимірювання часу руху світла виявляється зручним способом вимірювання відстаней.

В комп'ютерній техніці

У комп'ютерах швидкість світла накладає обмеження на швидкість передачі даних між процесорами. Якщо процесор працює на частоті 1 гігагерц, то за один такт сигнал встигає поширюватися не далі, ніж на 30 см. Тому процесори і мікросхеми пам'яті необхідно розміщувати близько один до одного, щоб мінімізувати затримки зв'язку. Якщо тактова частота продовжить збільшуватися, то швидкість світла зрештою може стати обмежуючим фактором для конструкції окремих мікросхем[58][59].

В наземному зв'язку

Оскільки довжина земного екватора становить близько 40 075 км, а c ≈ 300 000, то теоретично найкоротший час, за який сигнал проходить половину земної кулі вздовж поверхні, становить приблизно 67 мілісекунд. Коли світло поширюється в оптичному волокні? швидкість світла менша приблизно на 35 % в оптичному волокні, залежно від його показника заломлення n, і час проходження збільшується. Крім того, лінії зв'язку не є ідеально прямими. Додатково час подорожі збільшується, коли сигнали проходять через електронні комутатори або регенератори сигналів[60].

Хоча цей час затримки в більшості випадків неважливий, він відіграє роль в таких сферах, як високочастотна торгівля(інші мови), де трейдери прагнуть отримати дрібні переваги, доставляючи свої угоди на біржі на частки секунди раніше за інших трейдерів. Наприклад, трейдери прагнуть використовувати мікрохвильовий зв'язок, бо швидкість радіохвиль у повітрі більша за швидкість світла в оптоволокні[61][62].

На космічних відстанях

The diameter of the moon is about one quarter of that of Earth, and their distance is about thirty times the diameter of Earth. A beam of light starts from the Earth and reaches the Moon in about a second and a quarter.
Зображено світловий промінь, який рухається між Землею та Місяцем, проходячи цей шлях за 1,255 секунди.

Ще більшими бувають затримки сигналу у зв'язку з космічними апаратами. Наприклад, коли земна станція зв'язувалась з астронавтами на Місяці, затримка на шлях сигналу туди й назад складала понад 2,5 секунди, що викликало неминучі паузи між запитаннями й відповідями[63]. На дорогу від Землі до Марса світлу потрібно від 5 до 20 хвилин залежно від відносного розташування двох планет. Якби робот на поверхні Марса зіткнувся з проблемою, в центрі управляння на Землі дізнались би про це лише за 5-20 хвилин, а потім ще 5-20 хвилин знадобилося б, щоб команди від центру управління дійшли на Марс[64].

Шлях світлових та інших сигналів від віддалених астрономічних джерел займає набагато більше часу. Наприклад, потрібно 13 мільярдів років, щоб світло потрапило до Землі від таких далеких галактик, як зображені на Hubble Ultra Deep Field[65][66]. Ці фотографії зображують галактики такими, якими вони були 13 мільярдів років тому, коли вік Всесвіту був менше мільярда років[65]. Через скінченність швидкість світла більш віддалені об'єкти здаються молодшими, і це дозволяє астрономам робити висновки про еволюцію зір, галактик і самого Всесвіту[67].

Астрономічні відстані часто виражають в світлових роках[68]. Світловий рік — це відстань, яку проходить світло за один юліанський рік, приблизно 9461 мільярдів кілометрів, або 0,3066 парсека. Проксима Центавра, найближча до Землі зоря після Сонця, розміщена на відстані близько 4,2 світлового року від нас[69].

Вимірювання відстаней

Радарні системи вимірюють відстань до цілі за часом, який потрібен радіоімпульсу, щоб повернутися до антени радара після відбиття від цілі: відстань до цілі дорівнює половині часу проходження туди й назад, помноженому на швидкість світла. Приймачі GPS вимірюють відстань до супутників GPS на основі того, скільки часу потрібно радіосигналу для надходження від кожного супутника, і на основі цих відстаней обчислюється положення приймача. Тому що світло проходить близько 300000 (186000) за одну секунду, ці вимірювання малих часток секунди мають бути дуже точними. Сучасні космічні радари визначають відстані до Місяця[70], планет[71] і космічних кораблів[72] шляхом вимірювання часу проходження світла або радіоімпульсів туди й назад.

Вимірювання

Існують різні способи визначення значення c. Одним зі способів є вимірювання фактичної швидкості, з якою поширюються світлові хвилі, що можна зробити в різних астрономічних і земних установках. Також можна визначити c з інших фізичних законів, де воно фігурує, наприклад, шляхом визначення значень електромагнітних констант ε0 і μ0 і використання їх зв'язку з c. Історично найточніші результати були отримані шляхом окремого визначення частоти та довжини хвилі світлового променя, причому їх добуток дорівнює c.

У 1983 році метр був визначений як «довжина шляху, пройденого світлом у вакуумі протягом інтервалу часу 1⁄299792458 секунди»[73], і таким чином значення швидкості світла було зафіксовано на рівні 299 792 458 за визначенням. Тепер точні вимірювання швидкості світла дають точний еталон метра, а не точне значення c.

Астрономічні вимірювання

Вимірювання швидкості світла за запізненнями входжень Іо в тінь Юпітера

Космічний простір є зручним місцем для вимірювання швидкості світла завдяки його великим просторовим масштабам і майже ідеальному вакууму. Історично вдавалось досить точно виміряти час, необхідний світлу для проходження деякої відстані в Сонячній системі, (наприклад, радіуса земної орбіти), натомість як точно виразити цю космічну відстань в земних одиницях довжини виявлялось складнішим.

Оле Ремер використав астрономічні вимірювання, щоб зробити першу кількісну оцінку швидкості світла[en] в 1676 році[74][75]. Виміряні із Землі, періоди обертання супутників інших планети здавалися коротшими, коли вони наближались до Землі, і довшими, коли віддалялись. Величина запізнення обертання супутника визначалась часом, потрібним світлу, щоб пройти відстань від супутника до Землі. Ремер спостерігав цей ефект для Іо, внутрішнього великого супутника Юпітера, і з величини запізнень моментів його входження в тінь Юпітера зробив висновок, що світлу потрібно 11 хвилин, аби пройти відстань від Сонця до Землі[74].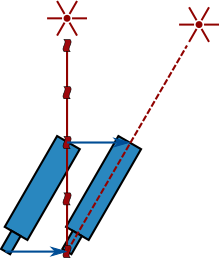

A star emits a light ray that hits the objective of a telescope. While the light travels down the telescope to its eyepiece, the telescope moves to the right. For the light to stay inside the telescope, the telescope must be tilted to the right, causing the distant source to appear at a different location to the right.
Аберація світла: для рухомого телескопа світло від віддаленого джерела виглядає так, ніби воно приходить з іншого місця

Інший метод полягає у використанні аберації світла, відкритої та поясненої Джеймсом Бредлі у XVIII столітті[76]. Цей ефект є результатом векторного додавання швидкості світла, що надходить від віддаленого джерела (наприклад, зорі), і швидкості руху спостерігача. Спостерігач бачить світло в напрямку, нахиленому вздовж його напрямку руху. Оскільки напрямок швидкості Землі постійно змінюється через обертання Землі навколо Сонця, видиме положення зір на небі теж змінюється, коливаючись протягом року в межах 20,5 кутових секунд[77]. У 1729 році Бредлі використовував цей метод, щоб вивести, що світло поширюється 10 210 разів швидше за швидкість орбітального руху Землі (сучасне значення — 10 066 разів). Знаючи період обертання Землі навколо Сонця, це дозволяло порахувати, що світлу потрібно 8 хвилин 12 секунд на шлях від Сонця до Землі[76].

Останнім часом вимірювання c в секундах на астрономічну одиницю виконувалось шляхом порівняння часу, протягом якого радіосигнали досягають різних космічних апаратів у Сонячній системі, з їхнім положенням, розрахованим за законами гравітації. У 2009 році на основі всіх попередніх вимірювань Міжнародний астрономічний союз рекомендував для часу проходження світлом середнього радіуса земної орбіти використовувати значення 499.004783836(10) с (трохи більше, ніж 8 хвилин 19 секунд)[78][79]. Відносна похибка цих вимірювань становить 2·10−11, і має той самий порядок, що й земні вимірювання довжини за допомогою інтерферометрії[80]. У 2012 році астрономічна одиниця була перевизначена як рівно 149597870700 м[81][82], що є гарним наближенням до значень, визначених у попередніх вимірюваннях[81]. Аналогічно сучасному визначенню метра, таке визначення фіксує точне числове значення швидкості світла в астрономічних одиницях на секунду[83].

Час поширення світла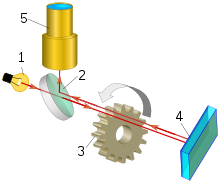

A light ray passes horizontally through a half-mirror and a rotating cog wheel, is reflected back by a mirror, passes through the cog wheel, and is reflected by the half-mirror into a monocular.
Схема апарату Фізо: 1 — джерело світла; 2 — напівпрозоре дзеркало; 3 — зубчасте колесо; 4 — далеке дзеркало; 5 — телескоп
Одне з останніх і найточніших вимірювань часу поширення світла, експеримент Майкельсона, Піза та Пірсона 1930–35 років. Використовувалось обертове дзеркало та вакуумна камера довжиною 1,6 км, яку світловий промінь проходив 10 разів. Точність становила ±11 км/с.

Цей метод вимірювання швидкості світла полягає у вимірюванні часу, необхідного світлу для проходження відомої відстані туди й назад. За цим принципом були проведені класичні експерименти Іпполіта Фізо та Леона Фуко.

В установці Фізо[en] світловий промінь направлявся на дзеркало на відстані 8 км. На шляху до дзеркала і назад промінь проходив через зубчасте обертове колесо. При певній швидкості обертання промінь по дорозі туди проходив через один проміжок між зубцями, а по дорозі назад — через наступний проміжок. Однак при трохи більших або менших швидкостях обертання промінь на зворотному шляху натикався на зубець і не доходив до спостерігача. Знаючи відстань між колесом і дзеркалом, кількість зубців на колесі та швидкість обертання, можна було розрахувати швидкість світла[84].

В методі Фуко[en] зубчасте колесо було замінене обертовим дзеркалом, яке встигало зробити частину оберту, поки світло рухалось до далекого дзеркала і назад, і тому на виході світло відбивалось під трохи іншим кутом, ніж на вході. З цієї різниці кутів обчислювалась швидкість світла[85]. За порадою Франсуа Араго, Фуко використовував свій прилад для вимірювання швидкості світла в повітрі й у воді[86].

В сучасних версіях цього методу використовують осцилографи з часовою роздільною здатністю менше однієї наносекунди, що дозволяє безпосередньо виміряти швидкість світла шляхом визначення часу затримки світлового імпульсу від лазера або світлодіода, відбитого від дзеркала. Цей метод дає похибки порядку 1 %, — гірше, ніж інші сучасні методи, однак його іноді використовують як лабораторний експеримент на університетських уроках фізики[9].

Електромагнітні константи

Спосіб визначення c, незалежний від вимірювання поширення електромагнітних хвиль, полягає у використанні співвідношення між c, електричною сталою ε0 і магнітною сталою μ0, встановленими теорією Максвелла: c2 = 1/(ε0μ0). Електричну сталу можна визначити шляхом вимірювання ємності та розмірів конденсатора, а магнітна стала зафіксована рівною 4π·10−7 Н/м через визначення ампера. Роза[de] та Дорсі[en] використали цей метод у 1907 році, щоб знайти значення с = 299710±22 км/с. Їхній метод залежав від наявності стандартної одиниці електричного опору, «міжнародного Ома», і тому його точність була обмежена тим, як цей стандарт був визначений[87][88].

Стоячі хвилі

A box with three waves in it; there are one and a half wavelength of the top wave, one of the middle one, and a half of the bottom one.
Електромагнітні стоячі хвилі в резонаторі

Ще один спосіб вимірювання швидкості світла полягає в незалежному вимірюванні частоти f і довжини хвилі λ електромагнітної хвилі у вакуумі. Тоді значення c можна знайти за формулою c = fλ. Одним із варіантів є вимірювання частот стоячих хвиль у резонансній порожнині, натомість як довжини хвиль розраховуються за розмірами порожнини. У 1946 році Луїс Ессен[en] і Гордон-Сміт встановили частоту для різноманітних нормальних мод хвиль мікрохвильового діапазону у резонансній порожнині. Її розміри були встановлені з точністю близько ±0,8 мкм за допомогою датчиків, відкаліброваних методами інтерферометрії[89]. Довжини хвиль були розраховані з геометрії резонатора та електромагнітної теорії, і з виміряних частот була розрахована швидкість світла[89][90].

Результати Ессена-Гордона-Сміта, 299792±9 км/с, були значно точнішими, ніж отримані оптичними методами[91]. До 1950 року повторні вимірювання Ессена покращили результат до 299792.5±3.0 км/с[92].

Цей метод можна навіть реалізувати в домашніх за допомогою мікрохвильової печі. Якщо зняти поворотну тарілку, щоб їжа не рухалася, то за плавленням їжі (наприклад, маргарину) можна буде визначити точки максимального нагріву — пучності стоячої хвилі. Відстань між двома пучностями становить половину довжини хвилі. Помноживши виміряну так довжину хвилі на частоту печі (зазвичай вказана на задній панелі духовки, найчастіше становить 2450 МГц), швидкість світла подекуди вдається визначити з похибкою менше 5 %[93][94].

Інтерферометрія

Schematic of the working of a Michelson interferometer.
Інтерферометричне визначення довжини. Ліворуч — конструктивна інтерференція, праворуч — деструктивна.

Інтерферометрія — ще один метод визначення довжини хвилі електромагнітного випромінювання для вимірювання швидкості світла. Когерентний промінь світла (наприклад, від лазера) з відомою частотою f розділяється на дві частини, які потім знову поєднуються. Змінюючи різницю ходу світла і спостерігаючи зміну інтерференційної картини, можна визначити довжину хвилі λ, а потім розрахувати швидкість світла c = λf.

До появи лазерної технології для інтерферометричних вимірювань швидкості світла використовувалися когерентні радіоджерела[95]. Інтерферометричне визначення довжини хвилі стає менш точним зі збільшенням довжини хвилі, тому точність експериментів була обмежена довгою довжиною хвилі радіохвиль (~ 4 мм). Точність можна підвищити, використовуючи світло з меншою довжиною хвилі, але тоді стає важко безпосередньо виміряти частоту[96].

Один зі способів вирішення цієї проблеми полягає в тому, щоб почати з низькочастотного сигналу, частоту якого можна точно виміряти, і з цього сигналу синтезувати все більш високочастотні сигнали, частоту яких потім можна зв'язати з вихідним сигналом. Потім на цю частоту може бути налаштований лазер, а його довжину хвилі можна визначити за допомогою інтерферометрії[97]. Цей метод створила група в Національному бюро стандартів США і в 1972 році з її допомогою виміряла швидкість світла з відносною похибкою 3,5·10−9[97][98].

Історія

До раннього нового періоду не було відомо, чи світло поширюється миттєво чи з дуже великою скінченною швидкістю. Вперше це питання обговорювалося ще в Стародавній Греції, потім про це питання сперечалися арабські та європейські вчені, доки Ремер не зробив перший розрахунок швидкості світла. Відтоді точність вимірювання швидкості світла поступово підвищувалась, поки в 1983 році вона не була фіксована на значенні рівно 299 792 458 м/с.

Історія вимірювань c (в м/с)
<1638 Галілей, закриті ліхтарі невизначено[99][100][101]:1252[Note 1]
<1667 Академія дель Чименто, закриті ліхтарі невизначено[101]:1253[102]
1675 Ремер та Гюйгенс, затемнення супутників Юпітера 220000000[103][104] −27 %
1729 Джеймс Бредлі,
аберація світла		 301000000[105] +0.40 %
1849 Іпполіт Фізо, зубчасте колесо 315000000[105] +5.1 %
1862 Леон Фуко, обертання дзеркала 298000000±500000[105] −0.60 %
1907 Роза і Дорсі, електромагнітні константи 299710000±30000[106][107] −280 ppm
1926 Альберт Майкельсон, обертання дзеркала 299796000±4000[108] +12 ppm
1950 Ессен і Гордон-Сміт, резонатор 299792500±3000[109] +0.14 ppm
1958 Фроом, радіоінтерферометрія 299792500±100[110] +0.14 ppm
1972 Евенсон та ін., лазерна інтерферометрія 299792456.2±1.1[111] −0.006 ppm
1983 17-та ГКМВ, визначення метра 299792458 (рівно)[17]

Рання історія

Емпедокл (бл. 490—430 рр. до н. е.) був першим, хто запропонував теорію світла[112] і стверджував, що світло має скінченну швидкість[113]. Він вважав, що світло рухається, а для руху потрібен певний час. Арістотель, навпаки, вважав світло не рухом, а чимось стаціонарним, і тому дозволяв його миттєве поширення[114]. Евклід і Птолемей розвивали емісійну теорію зору Емпедокла, за якою світло випромінюється з ока, таким чином уможливлюючи зір. Ґрунтуючись на цій теорії, Герон Александрійський стверджував, що швидкість світла має бути нескінченною, оскільки віддалені об'єкти, такі як зорі, стають видними відразу після відкриття очей[115].

Ранні ісламські філософи спочатку погоджувалися з аристотелівською точкою зору, що світло не має швидкості руху. У 1021 році Альгазен (Ібн аль-Хайсам) опублікував «Книгу оптики»(інші мови), в якій він спростовував емісійну теорію зору та доводив, що світло рухається від об'єкта до ока[116]. Це змусило Альгазена припустити, що світло має скінченну швидкість[117][118][119], і що ця швидкість є змінною, зменшуючись у щільніших тілах[119][120]. Він стверджував, що світло — це форма матерії, для поширення якої потрібен час, навіть якщо це приховано від почуттів[121]. Інший ісламський вчений XI століття, Абу Райхан аль-Біруні, погоджувався зі скінченністю швидкості світла, але наполягав, що швидкість світла набагато більша за швидкість звуку[122].

У XIII столітті Роджер Бекон стверджував, що швидкість світла в повітрі є скінченною, використовуючи філософські аргументи, підкріплені роботами Альгазена та Арістотеля[123][124]. У 1270-х роках Вітело розглядав можливість руху світла з нескінченною швидкістю у вакуумі і його сповільнення у щільніших тілах[125].

На початку XVII століття Йоганн Кеплер вважав, що швидкість світла нескінченна, оскільки порожній простір не є для нього перешкодою. Рене Декарт помилково стверджував, що якби швидкість світла була б скінченною, Сонце, Земля та Місяць не спостерігались би на одній прямій під час місячного затемнення[126]. Він вважав, що скінченність швидкості світла зруйнувало б усю його філософську систему[127], однак у своєму виведенні закону Снеліуса припускав, що якийсь пов'язаний зі світлом рух є швидшим у щільнішому середовищі[128][129]. Натомість П'єр Ферма підтримував скінченність швидкості світла й вивів закон Снелліуса, використовуючи протилежне припущення, що чим щільніше середовище, тим повільніше поширюється ним світло[130].

Перші спроби вимірювання

У 1629 році Ісаак Бікман запропонував експеримент, під час якого людина спостерігає спалах гармати, що відбивається від дзеркала на відстані однієї милі (1,6 км). У 1638 році Галілео Галілей описав експеримент, в якому двоє спостерігачів на великій відстані обмінювалися сигналами ліхтарів, визначаючи час затримки між надсиланням та отриманням сигналу. Галілей дійшов висновку, що швидкість світла набагато більша за можливості такого методу вимірювання[99][100]. У 1667 році Академія дель Чименто у Флоренції повідомила, що вона провела експеримент Галілея з ліхтарями, розділеними відстанню близько милі, але теж не змогла виміряти затримку[131], яка в цьому експерименті мала б становити близько 11 мікросекунд.

A diagram of a planet's orbit around the Sun and of a moon's orbit around another planet. The shadow of the latter planet is shaded.
Ілюстрація методу Ремера. Вгорі — орбіта Іо навколо Юпітера, внизу — орбіта Землі навколо Сонця.

Перша кількісна оцінка швидкості світла була зроблена в 1676 році Оле Ремером[132][133]. З огляду на те, що періоди внутрішнього супутника Юпітера Іо виявляються коротшими, коли Земля наближається до Юпітера, ніж коли вона віддаляється від нього, він зробив висновок, що світло поширюється зі скінченною швидкістю, і підрахував, що світлу потрібно 11 хвилин, щоб пройти радіус орбіти Землі. Крістіан Гюйгенс поєднав цю оцінку з оцінкою діаметра орбіти Землі і отримав значення швидкості світла 220000 км/с, що на 27 % менше істинного значення[134].

У своїй книзі «Оптика» 1704 року Ісаак Ньютон повідомив про розрахунки Ремера щодо скінченності швидкості світла та дав значення «сім або вісім хвилин» для часу, необхідного для проходження світла від Сонця до Землі (сучасне значення становить 8 хвилин 19 секунд)[135]. Ньютон запитав, чи тіні затемнення Ромера кольорові. Почувши, що це не так, він зробив висновок, що різні кольори рухаються з однаковою швидкістю. У 1729 році Джеймс Бредлі відкрив аберацію зоряного світла[136]. З цього ефекту він визначив, що світло має рухатися в 10 210 разів швидше, ніж орбітальний рух Землі (сучасне значення відношення швидкостей — 10 066 разів) або, що еквівалентно, що світлу потрібно 8 хвилин 12 секунд на шлях від Сонця до Землі[136].

Зв'язок з електромагнетизмом

У XIX столітті Іполит Фізо розробив метод визначення швидкості світла на основі вимірювань часу польоту на Землі та повідомив про значення 315000 км/с[137]. Його метод був вдосконалений Леоном Фуко, який отримав значення 298000 км/с у 1862 році[138]. У 1856 році Вільгельм Едуард Вебер і Рудольф Кольрауш виміряли співвідношення електромагнітних і електростатичних одиниць заряду, 1/√ε0μ0, розрядивши лейденську банку, і виявили, що його числове значення було дуже близьким до швидкості світло, виміряним Фізо. Наступного року Густав Кірхгоф підрахував, що з такою швидкістю поширюється електричний сигнал у дроті без опору[139].

На початку 1860-х Максвелл показав, що згідно з теорією електромагнетизму, над якою він працював, електромагнітні хвилі поширюються в порожньому просторі[9] зі швидкістю, що дорівнює наведеному вище відношенню Вебера-Кольрауша. Він звернув увагу на чисельну близькість цього значення швидкості світла, виміряної Фізо, і припустив, що світло є електромагнітною хвилею[140]. Максвелл підкріпив своє твердження власним експериментом, опублікованим у 1868 році у «Philosophical Transactions», який визначив співвідношення електростатичних і електромагнітних одиниць[141].

«Світлоносний ефір»

Альберт Ейнштейн і Гендрік Лоренц (1921)

У той час вважалося, що порожній простір заповнений фоновим середовищем, яке називалось світлоносним ефіром і мало передавати електромагнітне поле. Деякі фізики вважали, що цей ефір є сама тією системою відліку, відносно якої визначається швидкість світла, і тому можна виміряти рух Землі відносно цього середовища шляхом вимірювання залежності швидкості світла від напрямку поширення. Починаючи з 1880-х років було проведено кілька експериментів, щоб спробувати виявити цей рух, найвідомішим з яких є експеримент, проведений Альбертом Майкельсоном і Едвардом Морлі в 1887 році[142][143]. Виявлений рух завжди був меншим за похибку спостереження. Сучасні експерименти показують, що двостороння швидкість світла ізотропна (однакова в усіх напрямках) з точністю до 6 нанометрів на секунду[144].

На основі цьому експерименту Гендрік Лоренц припустив, що рух приладу в ефірі може спричинити скорочення приладу вздовж його довжини в напрямку руху, і він також припустив, що час у рухомих системах відліку також змінюється, що призвело до формулювання перетворення Лоренца. Базуючись на теорії ефіру Лоренца, Анрі Пуанкаре (1900) показав, що цей локальний час (у першому порядку за v/c) вказується годинниками, що рухаються в ефірі й синхронізовані за припущення сталої швидкості світла. У 1904 році він припустив, що швидкість світла може бути граничною швидкістю в динаміці за умови підтвердження всіх припущень теорії Лоренца. У 1905 році Пуанкаре привів теорію ефіру Лоренца в повну відповідність із принципом відносності[145][146].

Спеціальна теорія відносності

У 1905 році Ейнштейн постулював, що швидкість світла у вакуумі, виміряна спостерігачем в інерціальній системі відліку, не залежить від руху джерела або спостерігача. З цього постулату він вивів спеціальну теорію відносності, в якій швидкість світла у вакуумі c виступає як фундаментальна константа, яка проявляється також в явищах, ніяк не пов'язаних зі світлом. Це зробило марною концепцію нерухомого ефіру (якої все ще дотримувалися Лоренц і Пуанкаре) і революціонізувало концепції простору і часу[147][148].Підвищення точності c і перевизначення метра та секунди

Збільшення точності c і перевизначення метра та секунди

У другій половині XX століття був досягнутий значний прогрес у підвищенні точності вимірювань швидкості світла, спочатку за допомогою методу стоячих хвиль, а пізніше за допомогою методів лазерної інтерферометрії. Цьому сприяли нові, більш точні визначення метра та секунди. У 1950 році Луїс Ессен визначив швидкість як 299792.5±3.0 м/с, використовуючи метод стоячих хвиль[149]. Це значення було прийнято 12-ю Генеральною асамблеєю Радіонаукового союзу в 1957 році. У 1960 році метр було перевизначено(інші мови) через довжину хвилі конкретної спектральної лінії криптону-86, а в 1967 році було перевизначено секунду через частоту надтонкого переходу основного стану цезію-133[150].

У 1972 році, використовуючи метод лазерної інтерферометрії та нові визначення, група з Національного бюро стандартів США в Боулдері, штат Колорадо, визначила швидкість світла у вакуумі як c = 299792456.2±1.1 м/с. Це було в 100 разів точніше, ніж раніше прийняте значення. Тепер основна невизначеність була в основному пов'язана з визначенням метра[151]. Оскільки інші експерименти теж отримали подібні результати для c, 15-та Генеральна конференція мір і ваг у 1975 році рекомендувала використовувати значення 299792458 м/с для швидкості світла[152].

Фіксація числового значення c

У 1983 році на 17-му засіданні Генеральної конференції мір і ваг було встановлено, що довжини хвиль, отримані за допомогою вимірювань частоти за даного значення швидкості світла є більш відтворюваними, ніж попередній стандарт метра. Тому для секунди зберегли визначення 1967 року через надтонку структуру атома цезію, а метр перевизначили як «довжину шляху, пройденого світлом у вакуумі за часовий інтервал 299792458 секунди»[153].

В результаті цього визначення швидкість світла у вакуумі була зафіксована на значенні рівно 299792458 м/с[154][155] і стала визначеною константою в системі одиниць СІ[156]. Удосконалені експериментальні методи, за допомогою яких до 1983 року можна було вимірювати швидкість світла, більше не впливають на відоме значення швидкості світла в одиницях СІ, а натомість дозволяють точніше реалізувати метр шляхом точнішого вимірювання довжини хвилі криптону-86 та інших джерел світла[157][158].

У 2011 році Генеральна конференція мір і ваг оголосила про свій намір перевизначити всі сім базових одиниць СІ так, щоб кожна одиниця визначалась опосередковано шляхом фіксації точного значення загальновизнаної фундаментальної константи, як було зроблено для швидкості світла. Було запропоноване нове, але абсолютно еквівалентне формулювання визначення метра: «його величина встановлюється шляхом фіксації числового значення швидкості світла у вакуумі на значенні точно 299792458, коли її виражають в одиницях системи СІ м с−1»[159]. Це була одна зі змін, включених у зміни визначень базових одиниць системи СІ 2019 року, яку також називають «новою СІ»[47].

Див. також

Виноски

  1. ↑ Точне значення: (299792458 × 60 × 60 × 24 / 149597870700) AU/day
  2. ↑ Точне значення: (999992651 π / 10246429500) pc/y
  3. ↑ Однак, частота світла залежить від руху джерела світла відносно спостерігача, завдяки Ефекту Доплера
  4. ↑ У той час як рухомі виміри об'єктів виявляються коротшими по лінії відносного руху, вони також виглядають як начебто їх повертають. Цей ефект, відомий як обертання Террелла, пов'язаний із різницею в часі, який потрібен світлу від різних частин об'єкта для того, щоб досягти спостерігача[25][26]
  5. ↑ Вважається, що ефект Шарнгорста не дозволяє сигналам поширюватись швидше ніж  c, але особливі умови, за яких ефект може виникати, заважають застосувати цей ефект для порушення принципу причинності[38]
  1. ↑ According to Galileo, the lanterns he used were "at a short distance, less than a mile." Assuming the distance was not too much shorter than a mile, and that "about a thirtieth of a second is the minimum time interval distinguishable by the unaided eye", Boyer notes that Galileo's experiment could at best be said to have established a lower limit of about 60 miles per second for the velocity of light.[100]

Примітки

  1. ↑ а б Definitions of the SI base units. physics.nist.gov. 29 травня 2019. Процитовано 8 лютого 2022.
  2. ↑ Penrose, R (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage Books. с. 410–411. ISBN 978-0-679-77631-4. ... the most accurate standard for the metre is conveniently defined so that there are exactly 299792458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris.
  3. ↑ It is exact because, by a 1983 international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time interval of 1⁄299792458 second. This particular value was chosen to provide a more accurate definition of the metre that still agreed as much as possible with the definition used before. See, for example, the NIST website[1] or the explanation by Penrose.[2] The second is, in turn, defined to be the length of time occupied by 9192631770 cycles of the radiation emitted by a caesium-133 atom in a transition between two specified energy states.[1]
  4. ↑ Moses Fayngold (2008). Special Relativity and How it Works (вид. illustrated). John Wiley & Sons. с. 497. ISBN 978-3-527-40607-4.
  5. ↑ Albert Shadowitz (1988). Special Relativity (вид. revised). Courier Corporation. с. 79. ISBN 978-0-486-65743-1.
  6. ↑ Peres, Asher; Terno, Daniel R. (6 січня 2004). Quantum information and relativity theory. Reviews of Modern Physics (англ.). 76 (1): 93—123. arXiv:quant-ph/0212023. Bibcode:2004RvMP...76...93P. doi:10.1103/RevModPhys.76.93. ISSN 0034-6861.
  7. ↑ Gibbs, Philip (1997). How is the speed of light measured?. The Physics and Relativity FAQ. Архів оригіналу за 21 серпня 2015.
  8. ↑ Stachel, JJ (2002). Einstein from "B" to "Z" – Volume 9 of Einstein studies. Springer. с. 226. ISBN 978-0-8176-4143-6.
  9. ↑ а б в See, for example:
  10. ↑ Gibbs, P (2004) [1997]. Why is c the symbol for the speed of light?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 17 листопада 2009. Процитовано 16 листопада 2009. {{cite web}}: Cite має пустий невідомий параметр: |df= (довідка) «The origins of the letter c being used for the speed of light can be traced back to a paper of 1856 by Weber and Kohlrausch […] Weber apparently meant c to stand for 'constant' in his force law, but there is evidence that physicists such as Lorentz and Einstein were accustomed to a common convention that c could be used as a variable for velocity. This usage can be traced back to the classic Latin texts in which c stood for 'celeritas' meaning 'speed'.»
  11. ↑ Mendelson, KS (2006). The story of c. American Journal of Physics. 74 (11): 995—97. Bibcode:2006AmJPh..74..995M. doi:10.1119/1.2238887. ISSN 0002-9505.
  12. ↑ Див. наприклад:
  13. ↑ Шаблон:SIbrochure8th
  14. ↑ See, for example:
  15. ↑ Lawrie, ID (2002). Appendix C: Natural units. A Unified Grand Tour of Theoretical Physics (вид. 2nd). CRC Press. с. 540. ISBN 978-0-7503-0604-1.
  16. ↑ Hsu, L (2006). Appendix A: Systems of units and the development of relativity theories. A Broader View of Relativity: General Implications of Lorentz and Poincaré Invariance (вид. 2nd). World Scientific. с. 427–428. ISBN 978-981-256-651-5.
  17. ↑ а б Resolution 1 of the 17th CGPM. BIPM. 1983. Архів оригіналу за 23 червня 2013. Процитовано 23 серпня 2009.
  18. ↑ Stachel, JJ (2002). Einstein from "B" to "Z" – Volume 9 of Einstein studies. Springer. с. 226. ISBN 0-8176-4143-2. Архів оригіналу за 23 червня 2013. Процитовано 4 червня 2012.
  19. ↑ Einstein, A (1905). Zur Elektrodynamik bewegter Körper. Annalen der Physik (German) . 17: 890—921. doi:10.1002/andp.19053221004. English translation: Perrett, W; Jeffery, GB (tr.); Walker, J (ed.). On the Electrodynamics of Moving Bodies. Fourmilab[en]. Архів оригіналу за 1 лютого 2013. Процитовано 27 листопада 2009.
  20. ↑ Hsu, J-P; Zhang, YZ (2001). Lorentz and Poincaré Invariance. Advanced Series on Theoretical Physical Science. Т. 8. World Scientific. с. 543ff. ISBN 981-02-4721-4.
  21. ↑ а б Zhang, YZ (1997). Special Relativity and Its Experimental Foundations. Advanced Series on Theoretical Physical Science. Т. 4. World Scientific. с. 172–3. ISBN 981-02-2749-3. Процитовано 4 червня 2012.{{cite book}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання)
  22. ↑ d'Inverno, R (1992). Introducing Einstein's Relativity. Oxford University Press. с. 19–20. ISBN 0-19-859686-3.
  23. ↑ Sriranjan, B (2004). Postulates of the special theory of relativity and their consequences. The Special Theory to Relativity. PHI Learning. с. 20 ff. ISBN 81-203-1963-X. Архів оригіналу за 20 березня 2015. Процитовано 4 червня 2012.
  24. ↑ Roberts, T; Schleif, S; Dlugosz, JM (ed.) (2007). What is the experimental basis of Special Relativity?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 1 лютого 2013. Процитовано 27 листопада 2009.
  25. ↑ Terrell, J (1959). Invisibility of the Lorentz Contraction. Physical Review. 116 (4): 1041—5. Bibcode:1959PhRv..116.1041T. doi:10.1103/PhysRev.116.1041.
  26. ↑ Penrose, R (1959). The Apparent Shape of a Relativistically Moving Sphere. Proceedings of the Cambridge Philosophical Society. 55 (01): 137—9. Bibcode:1959PCPS...55..137P. doi:10.1017/S0305004100033776.
  27. ↑ Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. с. 52–9. ISBN 981-02-2749-3.
  28. ↑ Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. с. 332. ISBN 981-02-2749-3.
  29. ↑ The interpretation of observations on binary systems used to determine the speed of gravity is considered doubtful by some authors, leaving the experimental situation uncertain; seeSchäfer, G; Brügmann, MH (2008). Propagation of light in the gravitational filed of binary systems to quadratic order in Newton's gravitational constant: Part 3: ‘On the speed-of-gravity controversy’. У Dittus, H; Lämmerzahl, C; Turyshev, SG (ред.). Lasers, clocks and drag-free control: Exploration of relativistic gravity in space. Springer. ISBN 3-540-34376-8.
  30. ↑ Gibbs, P (1997) [1996]. Carlip, S (ред.). Is The Speed of Light Constant?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 17 листопада 2009. Процитовано 26 листопада 2009.
  31. ↑ Ellis, GFR; Uzan, J-P (2005). ‘c’ is the speed of light, isn’t it?. American Journal of Physics. 73 (3): 240—7. arXiv:gr-qc/0305099. Bibcode:2005AmJPh..73..240E. doi:10.1119/1.1819929. The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today.
  32. ↑ An overview can be found in the dissertation of Mota, DF (2006). Variations of the fine structure constant in space and time. arXiv:astro-ph/0401631. {{cite arXiv}}: Проігноровано |class= (довідка)
  33. ↑ Uzan, J-P (2003). The fundamental constants and their variation: observational status and theoretical motivations. Reviews of Modern Physics. 75 (2): 403. arXiv:hep-ph/0205340. Bibcode:2003RvMP...75..403U. doi:10.1103/RevModPhys.75.403.
  34. ↑ Amelino-Camelia, G (2008). Quantum Gravity Phenomenology. arXiv:0806.0339 [gr-qc].
  35. ↑ Herrmann, S та ін. (2009). Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level. Physical Review D. 80 (100): 105011. arXiv:1002.1284. Bibcode:2009PhRvD..80j5011H. doi:10.1103/PhysRevD.80.105011.
  36. ↑ Lang, KR (1999). Astrophysical formulae (вид. 3rd). Birkhäuser. с. 152. ISBN 3-540-29692-1.
  37. ↑ Fowler, M (March 2008). Notes on Special Relativity (PDF). University of Virginia. с. 56. Архів (PDF) оригіналу за 1 лютого 2013. Процитовано 7 травня 2010.
  38. ↑ Liberati, S; Sonego, S; Visser, M (2002). Faster-than-c signals, special relativity, and causality. Annals of Physics. 298 (1): 167—85. arXiv:gr-qc/0107091. Bibcode:2002AnPhy.298..167L. doi:10.1006/aphy.2002.6233.
  39. ↑ Taylor, EF; Wheeler, JA (1992). Spacetime Physics. W. H. Freeman. с. 74–5. ISBN 0-7167-2327-1.
  40. ↑ Tolman, RC (2009) [1917]. Velocities greater than that of light. The Theory of the Relativity of Motion (вид. Reprint). BiblioLife. с. 54. ISBN 978-1-103-17233-7.
  41. ↑ Hecht, E (1987). Optics (вид. 2nd). Addison-Wesley. с. 62. ISBN 978-0-201-11609-0.
  42. ↑ Quimby, RS (2006). Photonics and lasers: an introduction. John Wiley and Sons. с. 9. ISBN 978-0-471-71974-8.
  43. ↑ Wertheim, M (20 червня 2007). The Shadow Goes. The New York Times. Процитовано 21 серпня 2009.
  44. ↑ Gibbs, P (1997). Is Faster-Than-Light Travel or Communication Possible?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 10 березня 2010. Процитовано 20 серпня 2008.
  45. ↑ Gibbs, P (1997). Is Faster-Than-Light Travel or Communication Possible?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 10 березня 2010. Процитовано 20 серпня 2008.
  46. ↑ Gibbs, P (1997). Is Faster-Than-Light Travel or Communication Possible?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 10 March 2010. Процитовано 20 серпня 2008.
  47. ↑ а б See, for example:
  48. ↑ Muga, JG, ред. (2007). Time in Quantum Mechanics. Springer. с. 48. ISBN 978-3-540-73472-7.
  49. ↑ Hernández-Figueroa, HE; Zamboni-Rached, M; Recami, E (2007). Localized Waves. Wiley Interscience. с. 26. ISBN 978-0-470-10885-7.
  50. ↑ Wynne, K (2002). Causality and the nature of information. Optics Communications. 209 (1–3): 84—100. Bibcode:2002OptCo.209...85W. doi:10.1016/S0030-4018(02)01638-3.
  51. ↑ Reich, Eugenie Samuel (2 квітня 2012). Embattled neutrino project leaders step down. Nature News. doi:10.1038/nature.2012.10371. Процитовано 11 лютого 2022.
  52. ↑ OPERA Collaboration (12 липня 2012). Measurement of the neutrino velocity with the OPERA detector in the CNGS beam. Journal of High Energy Physics. 2012 (10): 93. arXiv:1109.4897. Bibcode:2012JHEP...10..093A. doi:10.1007/JHEP10(2012)093.
  53. ↑ Rees, M (1966). The Appearance of Relativistically Expanding Radio Sources. Nature. 211 (5048): 468. Bibcode:1966Natur.211..468R. doi:10.1038/211468a0.
  54. ↑ Chase, IP. Apparent Superluminal Velocity of Galaxies. Usenet Physics FAQ. University of California, Riverside. Процитовано 26 листопада 2009.
  55. ↑ Harrison, ER (2003). Masks of the Universe. Cambridge University Press. с. 206. ISBN 978-0-521-77351-5.
  56. ↑ Panofsky, WKH; Phillips, M (1962). Classical Electricity and Magnetism. Addison-Wesley. с. 182. ISBN 978-0-201-05702-7.
  57. ↑ Ellis, George F. R.; Williams, Ruth M. (2000). Flat and Curved Space-times (вид. 2nd). Oxford: Oxford University Press. с. 12. ISBN 0-19-850657-0. OCLC 44694623.
  58. ↑ Parhami, B (1999). Introduction to parallel processing: algorithms and architectures. Plenum Press. с. 5. ISBN 978-0-306-45970-2.
  59. ↑ . ISBN 978-3-642-03274-5. {{cite conference}}: Пропущений або порожній |title= (довідка)
  60. ↑ Theoretical vs real-world speed limit of Ping. Pingdom. June 2007. Архів оригіналу за 2 вересня 2010. Процитовано 5 травня 2010. [Архівовано 2010-09-02 у Wayback Machine.]
  61. ↑ Buchanan, Mark (11 лютого 2015). Physics in finance: Trading at the speed of light. Nature. 518 (7538): 161—163. Bibcode:2015Natur.518..161B. doi:10.1038/518161a. PMID 25673397.
  62. ↑ Time is money when it comes to microwaves. Financial Times. 10 травня 2013. Архів оригіналу за 10 грудня 2022. Процитовано 25 квітня 2014.
  63. ↑ Day 4: Lunar Orbits 7, 8 and 9. The Apollo 8 Flight Journal. NASA. Архів оригіналу за 4 січня 2011. Процитовано 16 грудня 2010.
  64. ↑ Communications. Mars 2020 Mission Perseverance Rover. NASA. Процитовано 14 березня 2020.
  65. ↑ а б (Пресреліз). {{cite press release}}: Пропущений або порожній |title= (довідка)
  66. ↑ The Hubble Ultra Deep Field Lithograph (PDF). NASA. Процитовано 4 лютого 2010.
  67. ↑ Mack, Katie (2021). The End of Everything (Astrophysically Speaking). London: Penguin Books. с. 18—19. ISBN 978-0-141-98958-7. OCLC 1180972461.
  68. ↑ The IAU and astronomical units. International Astronomical Union. Процитовано 11 жовтня 2010.
  69. ↑ Further discussion can be found at StarChild Question of the Month for March 2000. StarChild. NASA. 2000. Процитовано 22 серпня 2009.
  70. ↑ Dickey, JO та ін. (July 1994). Lunar Laser Ranging: A Continuing Legacy of the Apollo Program (PDF). Science. 265 (5171): 482—490. Bibcode:1994Sci...265..482D. doi:10.1126/science.265.5171.482. PMID 17781305.
  71. ↑ Standish, EM (February 1982). The JPL planetary ephemerides. Celestial Mechanics. 26 (2): 181—186. Bibcode:1982CeMec..26..181S. doi:10.1007/BF01230883.
  72. ↑ Berner, JB; Bryant, SH; Kinman, PW (November 2007). Range Measurement as Practiced in the Deep Space Network (PDF). Proceedings of the IEEE. 95 (11): 2202—2214. doi:10.1109/JPROC.2007.905128.
  73. ↑ Resolution 1 of the 17th CGPM. BIPM. 1983. Процитовано 23 серпня 2009.
  74. ↑ а б Cohen, IB (1940). Roemer and the first determination of the velocity of light (1676). Isis. 31 (2): 327—379. doi:10.1086/347594. {{cite journal}}: |hdl-access= вимагає |hdl= (довідка)
  75. ↑ Demonstration tovchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences [Demonstration to the movement of light found by Mr. Römer of the Royal Academy of Sciences] (PDF). Journal des sçavans (фр.): 233—236. 1676.
  76. ↑ а б Bradley, J (1729). Account of a new discovered Motion of the Fix'd Stars. Philosophical Transactions. 35: 637—660.
  77. ↑ Duffett-Smith, P (1988). Practical Astronomy with your Calculator. Cambridge University Press. с. 62. ISBN 978-0-521-35699-2.
  78. ↑ See the following:
  79. ↑ IAU Working Group on Numerical Standards for Fundamental Astronomy. IAU WG on NSFA Current Best Estimates. US Naval Observatory. Архів оригіналу за 8 грудня 2009. Процитовано 25 вересня 2009.
  80. ↑ NPL's Beginner's Guide to Length. UK National Physical Laboratory. Архів оригіналу за 31 серпня 2010. Процитовано 28 жовтня 2009.
  81. ↑ а б Resolution B2 on the re-definition of the astronomical unit of length (PDF). International Astronomical Union. 2012.
  82. ↑ Supplement 2014: Updates to the 8th edition (2006) of the SI Brochure (PDF). The International System of Units. International Bureau of Weights and Measures: 14. 2014.
  83. ↑ Brumfiel, Geoff (14 вересня 2012). The astronomical unit gets fixed. Nature (англ.). doi:10.1038/nature.2012.11416. ISSN 1476-4687.
  84. ↑ Gibbs, P (1997). How is the speed of light measured?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 21 серпня 2015. Процитовано 13 січня 2010.
  85. ↑ Fowler, M. The Speed of Light. University of Virginia. Процитовано 21 квітня 2010.
  86. ↑ Hughes, Stephan (2012). Catchers of the Light: The Forgotten Lives of the Men and Women Who First Photographed the Heavens. ArtDeCiel Publishing. с. 210. ISBN 978-1-62050-961-6.
  87. ↑ Essen, L; Gordon-Smith, AC (1948). The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator. Proceedings of the Royal Society of London A. 194 (1038): 348—361. Bibcode:1948RSPSA.194..348E. doi:10.1098/rspa.1948.0085. JSTOR 98293.
  88. ↑ Rosa, EB; Dorsey, NE (1907). A new determination of the ratio of the electromagnetic to the electrostatic unit of electricity. Bulletin of the Bureau of Standards. 3 (6): 433. doi:10.6028/bulletin.070.
  89. ↑ а б Essen, L; Gordon-Smith, AC (1948). The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator. Proceedings of the Royal Society of London A. 194 (1038): 348—361. Bibcode:1948RSPSA.194..348E. doi:10.1098/rspa.1948.0085. JSTOR 98293.
  90. ↑ Essen, L (1947). Velocity of Electromagnetic Waves. Nature. 159 (4044): 611—612. Bibcode:1947Natur.159..611E. doi:10.1038/159611a0.
  91. ↑ Essen, L; Gordon-Smith, AC (1948). The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator. Proceedings of the Royal Society of London A. 194 (1038): 348—361. Bibcode:1948RSPSA.194..348E. doi:10.1098/rspa.1948.0085. JSTOR 98293.
  92. ↑ Essen, L (1950). The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator. Proceedings of the Royal Society of London A. 204 (1077): 260—277. Bibcode:1950RSPSA.204..260E. doi:10.1098/rspa.1950.0172. JSTOR 98433.
  93. ↑ Stauffer, RH (April 1997). Finding the Speed of Light with Marshmallows. The Physics Teacher. 35 (4): 231. Bibcode:1997PhTea..35..231S. doi:10.1119/1.2344657. Процитовано 15 лютого 2010.
  94. ↑ BBC Look East at the speed of light. BBC Norfolk website. Процитовано 15 лютого 2010.
  95. ↑ Froome, KD (1958). A New Determination of the Free-Space Velocity of Electromagnetic Waves. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 247 (1248): 109—122. Bibcode:1958RSPSA.247..109F. doi:10.1098/rspa.1958.0172. JSTOR 100591.
  96. ↑ Sullivan, DB (2001). Speed of Light from Direct Frequency and Wavelength Measurements. У Lide, DR (ред.). A Century of Excellence in Measurements, Standards, and Technology (PDF). CRC Press. с. 191—193. ISBN 978-0-8493-1247-2. Архів оригіналу (PDF) за 13 серпня 2009. [Архівовано 2009-08-13 у Wayback Machine.]
  97. ↑ а б Sullivan, DB (2001). Speed of Light from Direct Frequency and Wavelength Measurements. У Lide, DR (ред.). A Century of Excellence in Measurements, Standards, and Technology (PDF). CRC Press. с. 191—193. ISBN 978-0-8493-1247-2. Архів оригіналу (PDF) за 13 серпня 2009. [Архівовано 2009-08-13 у Wayback Machine.]
  98. ↑ Evenson, KM та ін. (1972). Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser. Physical Review Letters. 29 (19): 1346—1349. Bibcode:1972PhRvL..29.1346E. doi:10.1103/PhysRevLett.29.1346.
  99. ↑ а б Galilei, G (1954). Dialogues Concerning Two New Sciences. Dover Publications. с. 43. ISBN 978-0-486-60099-4. Архів оригіналу за 30 січня 2019. Процитовано 29 січня 2019. [Архівовано 2019-01-30 у Wayback Machine.]
  100. ↑ а б в Boyer, CB (1941). Early Estimates of the Velocity of Light. Isis. 33 (1): 24. doi:10.1086/358523.
  101. ↑ а б Foschi, Renato; Leone, Matteo (2009), Galileo, measurement of the velocity of light, and the reaction times, Perception, 38 (8): 1251—1259, doi:10.1068/p6263, hdl:2318/132957, PMID 19817156, S2CID 11747908
  102. ↑ Magalotti, Lorenzo (2001) [1667], Saggi di Naturali Esperienze fatte nell' Accademia del Cimento (вид. digital, online), Florence: Istituto e Museo di Storia delle Scienze, с. 265–266, процитовано 25 вересня 2015
  103. ↑ Touchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences (PDF). Journal des sçavans (French) : 233—36. 1676. Архів оригіналу (PDF) за 21 липня 2011. Процитовано 28 січня 2011.
  104. ↑ Huygens, C (1690). Traitée de la Lumière (French) . Pierre van der Aa. с. 8—9.
  105. ↑ а б в Gibbs, P (1997). How is the speed of light measured?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 23 червня 2013. Процитовано 13 січня 2010.
  106. ↑ Essen, L; Gordon-Smith, AC (1948). The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator. Proceedings of the Royal Society of London A. 194 (1038): 348—361. Bibcode:1948RSPSA.194..348E. doi:10.1098/rspa.1948.0085. JSTOR 98293.
  107. ↑ Rosa, EB; Dorsey, NE (1907). The Ratio of the Electromagnetic and Electrostatic Units. Bulletin of the Bureau of Standards. 3: 433. doi:10.1103/PhysRevSeriesI.22.367.
  108. ↑ Michelson, A. A. (1927). Measurement of the Velocity of Light Between Mount Wilson and Mount San Antonio. The Astrophysical Journal. 65: 1. Bibcode:1927ApJ....65....1M. doi:10.1086/143021.
  109. ↑ Essen, L (1950). The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator. Proceedings of the Royal Society of London A. 204 (1077): 260—277. Bibcode:1950RSPSA.204..260E. doi:10.1098/rspa.1950.0172. JSTOR 98433.
  110. ↑ Froome, KD (1958). A New Determination of the Free-Space Velocity of Electromagnetic Waves. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences,. The Royal Society. 247 (1248): 109—122. doi:10.1098/rspa.1958.0172. JSTOR 100591.
  111. ↑ Evenson, KM; et al. (1972). Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser. Physical Review Letters. 29: 1346—49. doi:10.1103/PhysRevLett.29.1346.
  112. ↑ Weiner, John; Nunes, Frederico (2013). Light-Matter Interaction: Physics and Engineering at the Nanoscale (вид. illustrated). OUP Oxford. с. 1. ISBN 978-0-19-856766-0.
  113. ↑ Sarton, G (1993). Ancient science through the golden age of Greece. Courier Dover. с. 248. ISBN 978-0-486-27495-9.
  114. ↑ MacKay, RH; Oldford, RW (2000). Scientific Method, Statistical Method and the Speed of Light. Statistical Science. 15 (3): 254—278. doi:10.1214/ss/1009212817.
  115. ↑ Ahmed, Sherif Sayed (2014). Electronic Microwave Imaging with Planar Multistatic Arrays. Logos Verlag Berlin. с. 1. ISBN 978-3-8325-3621-3.
  116. ↑ Gross, CG (1999). The Fire That Comes from the Eye. Neuroscientist. 5: 58—64. doi:10.1177/107385849900500108.
  117. ↑ MacKay, RH; Oldford, RW (2000). Scientific Method, Statistical Method and the Speed of Light. Statistical Science. 15 (3): 254—278. doi:10.1214/ss/1009212817.
  118. ↑ Hamarneh, S (1972). Review: Hakim Mohammed Said, Ibn al-Haitham. Isis. 63 (1): 119. doi:10.1086/350861.
  119. ↑ а б Lester, PM (2005). Visual Communication: Images With Messages. Thomson Wadsworth. с. 10—11. ISBN 978-0-534-63720-0.
  120. ↑ O'Connor, JJ; Robertson, EF. Abu Ali al-Hasan ibn al-Haytham. MacTutor History of Mathematics archive. University of St Andrews. Процитовано 12 січня 2010.
  121. ↑ . Keszthely, Hungary. {{cite conference}}: |archive-date= вимагає |archive-url= (довідка); Вказано більш, ніж один |archivedate= та |archive-date= (довідка); Пропущений або порожній |title= (довідка)Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання)
  122. ↑ O'Connor, JJ; Robertson, EF. Abu han Muhammad ibn Ahmad al-Biruni. MacTutor History of Mathematics archive. University of St Andrews. Процитовано 12 січня 2010.
  123. ↑ Lindberg, DC (1996). Roger Bacon and the origins of Perspectiva in the Middle Ages: a critical edition and English translation of Bacon's Perspectiva, with introduction and notes. Oxford University Press. с. 143. ISBN 978-0-19-823992-5.
  124. ↑ Lindberg, DC (1974). Late Thirteenth-Century Synthesis in Optics. У Edward Grant (ред.). A source book in medieval science. Harvard University Press. с. 396. ISBN 978-0-674-82360-0.
  125. ↑ Marshall, P (1981). Nicole Oresme on the Nature, Reflection, and Speed of Light. Isis. 72 (3): 357–374 [367–374]. doi:10.1086/352787.
  126. ↑ Sakellariadis, Spyros (1982). Descartes' Experimental Proof of the Infinite Velocity of Light and Huygens' Rejoinder. Archive for History of Exact Sciences. 26 (1): 1—12. doi:10.1007/BF00348308. ISSN 0003-9519. JSTOR 41133639.
  127. ↑ MacKay, RH; Oldford, RW (2000). Scientific Method, Statistical Method and the Speed of Light. Statistical Science. 15 (3): 254—278. doi:10.1214/ss/1009212817.
  128. ↑ Cajori, Florian (1922). A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories (англ.). Macmillan. с. 76.
  129. ↑ Smith, A. Mark (1987). Descartes's Theory of Light and Refraction: A Discourse on Method. Transactions of the American Philosophical Society. 77 (3): i—92. doi:10.2307/1006537. ISSN 0065-9746. JSTOR 1006537.
  130. ↑ Boyer, Carl Benjamin (1959). The Rainbow: From Myth to Mathematics. Thomas Yoseloff. с. 205—206. OCLC 763848561.
  131. ↑ Foschi, Renato; Leone, Matteo (August 2009). Galileo, Measurement of the Velocity of Light, and the Reaction Times. Perception (англ.). 38 (8): 1251—1259. doi:10.1068/p6263. ISSN 0301-0066. PMID 19817156. {{cite journal}}: |hdl-access= вимагає |hdl= (довідка)
  132. ↑ Cohen, IB (1940). Roemer and the first determination of the velocity of light (1676). Isis. 31 (2): 327—379. doi:10.1086/347594. {{cite journal}}: |hdl-access= вимагає |hdl= (довідка)
  133. ↑ Demonstration tovchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences [Demonstration to the movement of light found by Mr. Römer of the Royal Academy of Sciences] (PDF). Journal des sçavans (фр.): 233—236. 1676.
  134. ↑ Huygens, C (1690). Traitée de la Lumière (фр.). Pierre van der Aa. с. 8–9.
  135. ↑ Newton, I (1704). Prop. XI. Optiks.
  136. ↑ а б Bradley, J (1729). Account of a new discovered Motion of the Fix'd Stars. Philosophical Transactions. 35: 637—660.
  137. ↑ Guarnieri, M. (2015). Two Millennia of Light: The Long Path to Maxwell's Waves. IEEE Industrial Electronics Magazine. 9 (2): 54—56, 60. doi:10.1109/MIE.2015.2421754.
  138. ↑ Gibbs, P (1997). How is the speed of light measured?. Usenet Physics FAQ. University of California, Riverside. Архів оригіналу за 21 серпня 2015. Процитовано 13 січня 2010.
  139. ↑ Kirchhoff, G (1857). Über die Bewegung der Elektricität. Ann. Phys. 178 (12): 529—244. Bibcode:1857AnP...178..529K. doi:10.1002/andp.18571781203.
  140. ↑ O'Connor, JJ; Robertson, EF (November 1997). James Clerk Maxwell. School of Mathematics and Statistics, University of St Andrews. Архів оригіналу за 28 січня 2011. Процитовано 13 жовтня 2010.
  141. ↑ Campbell, Lewis, Garnett, William, Rautio, James C., The Life of James Clerk Maxwell, p.544, ISBN 978-1773751399.
  142. ↑ Consoli, Maurizio; Pluchino, Alessandro (2018). Michelson-Morley Experiments: An Enigma for Physics & The History of Science. World Scientific. с. 118—119. ISBN 978-9-813-27818-9. Процитовано 4 травня 2020.
  143. ↑ Michelson, AA; Morley, EW (1887). On the Relative Motion of the Earth and the Luminiferous Ether. American Journal of Science. 34 (203): 333—345. doi:10.1366/0003702874447824.
  144. ↑ French, AP (1983). Special relativity. Van Nostrand Reinhold. с. 51—57. ISBN 978-0-442-30782-0.
  145. ↑ Darrigol, O (2000). Electrodynamics from Ampére to Einstein. Clarendon Press. ISBN 978-0-19-850594-5.
  146. ↑ Galison, P (2003). Einstein's Clocks, Poincaré's Maps: Empires of Time. W.W. Norton. ISBN 978-0-393-32604-8.
  147. ↑ Miller, AI (1981). Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Addison–Wesley. ISBN 978-0-201-04679-3.
  148. ↑ Pais, A (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. ISBN 978-0-19-520438-4.
  149. ↑ Essen, L (1950). The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator. Proceedings of the Royal Society of London A. 204 (1077): 260—277. Bibcode:1950RSPSA.204..260E. doi:10.1098/rspa.1950.0172. JSTOR 98433.
  150. ↑ Resolution 1 of the 15th CGPM. BIPM. 1967. Архів оригіналу за 11 квітня 2021. Процитовано 14 березня 2021. [Архівовано 2021-04-11 у Wayback Machine.]
  151. ↑ Evenson, KM та ін. (1972). Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser. Physical Review Letters. 29 (19): 1346—1349. Bibcode:1972PhRvL..29.1346E. doi:10.1103/PhysRevLett.29.1346.
  152. ↑ Resolution 2 of the 15th CGPM. BIPM. 1975. Процитовано 9 вересня 2009.
  153. ↑ Resolution 1 of the 17th CGPM. BIPM. 1983. Процитовано 23 серпня 2009.
  154. ↑ Taylor, EF; Wheeler, JA (1992). Spacetime Physics: Introduction to Special Relativity (вид. 2nd). Macmillan. с. 59. ISBN 978-0-7167-2327-1.
  155. ↑ Penzes, WB (2009). Time Line for the Definition of the Meter (PDF). NIST. Процитовано 11 січня 2010.
  156. ↑ See, for example:
  157. ↑ Adams, S (1997). Relativity: An Introduction to Space–Time Physics. CRC Press. с. 140. ISBN 978-0-7484-0621-0. One peculiar consequence of this system of definitions is that any future refinement in our ability to measure c will not change the speed of light (which is a defined number), but will change the length of the meter!
  158. ↑ Rindler, W (2006). Relativity: Special, General, and Cosmological (вид. 2nd). Oxford University Press. с. 41. ISBN 978-0-19-856731-8. Note that [...] improvements in experimental accuracy will modify the meter relative to atomic wavelengths, but not the value of the speed of light!
  159. ↑ The "explicit-constant" formulation. BIPM. 2011. Архів оригіналу за 11 серпня 2014.

Посилання

Фізика Це незавершена стаття з фізики.
Ви можете допомогти проєкту, виправивши або дописавши її.
Kembali kehalaman sebelumnya