Обробка зображень

Обро́бка зобра́жень — будь-яка форма обробки інформації, для якої вхідні дані представлені зображенням, наприклад, фотографіями або відеокадрами. Обробляння зображень може здійснюватися як для отримання зображення на виході (наприклад, підготовка до поліграфічного тиражування, до телетрансляції і т. д.), так і для отримання іншої інформації (наприклад, розпізнання тексту, підрахунок числа і типу клітин в полі мікроскопа і т. д.). Крім статичних двомірних зображень, обробляти потрібно також зображення, що змінюються з часом, наприклад відео.

Ще в середині XX століття обробка зображень була здебільшого аналоговою і виконувалась оптичними пристроями. Подібні оптичні методи досі важливі, в таких областях як, наприклад, голографія. Тим не менш, з різким зростанням продуктивності комп'ютерів, ці методи все в більшій мірі витіснялися методами цифрової обробки зображень. Методи цифрової обробки зображень зазвичай є більш точними, надійними, гнучкими і простими в реалізації, ніж аналогові методи. У цифровій обробці зображень широко застосовується спеціалізоване обладнання, таке як процесори з конвеєрною обробкою інструкцій та багатопроцесорні системи. Особливою мірою це стосується систем обробки відео. Обробка зображень виконується також за допомогою програмних засобів комп'ютерної математики, наприклад, MATLAB, Mathcad, Maple, Mathematica і інш. Для цього в них використовуються як базові засоби, так і пакети розширення Image Processing.

Багато методів цифрової обробки зображень, або цифрової обробки зображень, як її часто називали, були розроблені в 1960-х роках у лабораторіях Белла, лабораторії реактивного руху, Массачусетському технологічному інституті, University_of_Maryland,_College_Park та кількох інших дослідницьких установах, із застосуванням до супутникових зображень, перетворення стандартів дротових фото, медичних зображень, відеотелефону, розпізнавання символів та покращення фотографій.[3] Метою ранньої обробки зображень було покращення якості зображення. Це було спрямовано на людей, щоб покращити візуальний ефект людей. При обробці зображень на вході виходить зображення низької якості, а на виході – зображення покращеної якості. Загальна обробка зображень включає покращення зображення, відновлення, кодування та стиснення. Першою успішною заявкою стала Американська лабораторія реактивного руху (JPL). Вони використовували такі методи обробки зображень, як геометрична корекція, трансформація градації, видалення шуму тощо на тисячах місячних фотографій, надісланих космічним детектором Ranger 7 у 1964 році, враховуючи положення Сонця та оточення Місяця. Вплив успішного комп’ютерного картографування карти поверхні Місяця був успішним. Пізніше було виконано більш складну обробку зображень майже 100 000 фотографій, надісланих назад космічним кораблем, щоб отримати топографічну карту, кольорову карту та панорамну мозаїку Місяця, що дозволило досягти надзвичайних результатів і закласти міцну основу для висадки людини на Землю. Місяць.[4]

Однак вартість обробки була досить високою з обчислювальним обладнанням того часу. Це змінилося в 1970-х роках, коли цифрова обробка зображень поширилася, оскільки стали доступними дешевші комп’ютери та спеціальне обладнання. Це призвело до того, що зображення оброблялися в режимі реального часу для деяких спеціальних проблем, таких як перетворення телевізійних стандартів. У міру того, як комп’ютери загального призначення стали швидшими, вони почали виконувати роль спеціального апаратного забезпечення для всіх операцій, крім найбільш спеціалізованих і інтенсивних комп’ютерних операцій. З появою швидких комп’ютерів і сигнальних процесорів у 2000-х роках цифрова обробка зображень стала найпоширенішою формою обробки зображень і зазвичай використовується, оскільки це не лише найуніверсальніший метод, але й найдешевший.

Основою для сучасних датчиків зображення є технологія метал-оксид-напівпровідник (MOS), яка бере свій початок із винаходу MOSFET (MOS-польового транзистора) Мохамедом М. Аталлою та Давоном Кангом у Bell Labs у 1959 році. Це призвело до розробки цифрових напівпровідникових датчиків зображення, включаючи пристрій із зарядовим зв'язком (CCD), а пізніше датчик CMOS.

Пристрій із зарядовим зв’язком був винайдений Уіллардом С. Бойлем і Джорджем Е. Смітом у Bell Labs у 1969 році. Досліджуючи технологію MOS, вони зрозуміли, що електричний заряд є аналогією магнітної бульбашки і що він може зберігатися на крихітному MOS-конденсаторі. Оскільки виготовити серію MOS-конденсаторів у ряд було досить просто, вони підключили до них відповідну напругу, щоб заряд міг передаватись від одного до іншого.CCD - це напівпровідникова схема, яка пізніше була використана в перших цифрових відеокамерах для телевізійного мовлення.[8]

Активний піксельний сенсор NMOS (APS) був винайдений Olympus у Японії в середині 1980-х років. Це стало можливим завдяки прогресу у виготовленні МОП-напівпровідникових пристроїв, коли масштабування МОП-транзисторів досягало менших мікронних, а потім субмікронних рівнів. NMOS APS був виготовлений командою Цутому Накамури на Olympus у 1985 році. Датчик CMOS з активними пікселями (CMOS-датчик) пізніше був розроблений командою Еріка Фоссума в Лабораторії реактивного руху НАСА в 1993 році. До 2007 року продажі датчиків CMOS перевищили датчики CCD.

Фільтрація

Цифрові фільтри використовуються для розмиття та підсилення цифрових зображень. Фільтрацію можна виконати за допомогою:

• конволюції з спеціально розробленими ядрами (масивами фільтрів) в просторовому домені.

• маскування конкретних частотних областей в частотному (Фур'є) домені.

Основна стаття: Цифровий сигнальний процесор

Електронна обробка сигналів стала революцією завдяки широкому впровадженню технології MOS у 1970-х роках.Технологія інтегральних схем MOS була основою для перших однокристальних мікропроцесорів і мікроконтролерів на початку 1970-х років , а потім перших однокристальних мікросхем цифрового сигнального процесора (DSP) наприкінці 1970-х років. Мікросхеми DSP з тих пір широко використовуються в цифровій обробці зображень.

Алгоритм стиснення зображення дискретного косинусного перетворення (DCT) широко реалізований у мікросхемах DSP, і багато компаній розробляють мікросхеми DSP на основі технології DCT. DCT широко використовуються для кодування, декодування, кодування відео, кодування аудіо, мультиплексування, сигналів керування, сигналізації, аналого-цифрового перетворення, форматування яскравості та відмінностей кольорів, а також форматів кольорів, таких як YUV444 та YUV411. DCT також використовуються для таких операцій кодування, як оцінка руху, компенсація руху, міжкадрове передбачення, квантування, перцептивне зважування, ентропійне кодування, змінне кодування та вектори руху, а також операцій декодування, таких як зворотна операція між різними форматами кольорів (YIQ, YUV і RGB) для відображення. DCT також широко використовуються для мікросхем кодера/декодера телебачення високої чіткості (HDTV).

Додаткова інформація: Медична візуалізація

У 1972 році інженер британської компанії EMI Housfield винайшов рентгенівський комп'ютерний томограф для діагностики голови, який прийнято називати КТ (комп'ютерна томографія). Метод КТ-ядра базується на проекції розрізу голови людини та обробляється комп’ютером для реконструкції зображення поперечного перерізу, що називається реконструкцією зображення. У 1975 році EMI успішно розробила пристрій КТ для всього тіла, який отримав чітке томографічне зображення різних частин людського тіла. У 1979 році ця діагностична методика отримала Нобелівську премію.Технологія обробки цифрових зображень для медичних застосувань була введена до Зали слави космічних технологій Space Foundation у 1994 році.

Більшість методів обробки одновимірних сигналів (наприклад, медіанний фільтр) застосовні і до двомірних сигналів, якими є зображення. Деякі з цих одновимірних методів значно ускладнюються з переходом до двовимірних сигналів. Обробка зображень вносить сюди кілька нових понять, таких як зв'язність і ротаційна інваріантність, які мають сенс тільки для двомірних сигналів. У обробці сигналів широко використовуються перетворення Фур'є, а також вейвлет-перетворення і фільтр Габора. Обробку зображень поділяють на обробку в просторовій області (перетворення яскравості, гама-корекція і т. д.) і частотній (перетворення Фур'є, і т. д.). Перетворення Фур'є дискретної функції (зображення) просторових координат є періодичним по просторових частотах з періодом 2pi.

Цифрова обробка зображень дозволяє використовувати складніші алгоритми, а отже, може запропонувати як більш складний результат у простих завданнях, так і реалізацію методів, які були б неможливі за допомогою аналогових засобів.

• Геометричні перетворення, такі як обертання і масштабування.
• Колірна корекція: зміна яскравості і контрасту, квантування кольору, перетворення в інший колірний простір.
• Порівняння двох і більше зображень. Як окремий випадок — знаходження кореляції між зображенням і зразком, наприклад, в детекторі банкнот.
• Комбінування зображень різними способами.
• Інтерполяція і згладжування.
• Поділ зображення на області (сегментація зображень), наприклад, для спрощення передачі каналами зв'язку^[1].
• Редагування та ретушування.
• Розширення динамічного діапазону шляхом комбінування зображень з різною експозицією (HDR).
• Компенсація втрати різкості, наприклад, шляхом нерізкого маскування.

Наведені нижче приклади демонструють обидва методи:

Filter type	Kernel or mask	Example
Original Image	${\displaystyle {\begin{bmatrix}0&0&0\\0&1&0\\0&0&0\end{bmatrix}}}$
Spatial Lowpass	${\displaystyle {\frac {1}{9}}\times {\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}}}$
Spatial Highpass	${\displaystyle {\begin{bmatrix}0&-1&0\\-1&4&-1\\0&-1&0\end{bmatrix}}}$
Fourier Representation	Pseudo-code: image = checkerboard F = Fourier Transform of image Show Image: log(1+Absolute Value(F))
Fourier Lowpass
Fourier Highpass

Zero padded	Repeated edge padded

Зверніть увагу, що фільтр високих частот показує додаткові краї, коли доповнено нулем, порівняно з повторним доповненням країв.

Приклади коду фільтрації

Приклад MATLAB для високочастотної фільтрації просторової області.

img=checkerboard(20);                           % generate checkerboard
% **************************  SPATIAL DOMAIN  ***************************
klaplace=[0 -1 0; -1 5 -1;  0 -1 0];             % Laplacian filter kernel
X=conv2(img,klaplace);                          % convolve test img with
                                                % 3x3 Laplacian kernel
figure()
imshow(X,[])                                    % show Laplacian filtered
title('Laplacian Edge Detection')

Щоб застосувати афінну матрицю до зображення, зображення перетворюється на матрицю, у якій кожен запис відповідає інтенсивності пікселів у цьому місці. Тоді розташування кожного пікселя можна представити як вектор, що вказує координати цього пікселя на зображенні, [x, y], де x і y — рядок і стовпець пікселя в матриці зображення. Це дозволяє помножити координату на матрицю афінного перетворення, яка дає позицію, куди буде скопійовано значення пікселя у вихідному зображенні.

Однак, щоб дозволити перетворення, які потребують перетворень трансляції, потрібні тривимірні однорідні координати. Для третього розміру зазвичай встановлюється ненульова постійна, зазвичай 1, так що нова координата дорівнює [x, y, 1]. Це дозволяє помножити координатний вектор на матрицю 3 на 3, уможливлюючи трансляційні зсуви. Отже, третій вимір, який є константою 1, дозволяє переклад.

Оскільки множення матриць є асоціативним, кілька афінних перетворень можна об’єднати в одне афінне перетворення шляхом множення матриці кожного окремого перетворення в тому порядку, у якому ці перетворення виконуються. Це призводить до єдиної матриці, яка, застосована до точкового вектора, дає той самий результат, що й усі окремі перетворення, виконані на векторі [x, y, 1] послідовно. Таким чином, послідовність матриць афінного перетворення може бути зведена до однієї матриці афінного перетворення.

Наприклад, двовимірні координати дозволяють лише обертання навколо початку координат (0, 0). Але тривимірні однорідні координати можна використовувати, щоб спочатку перевести будь-яку точку в (0, 0), потім виконати поворот і, нарешті, перевести початок координат (0, 0) назад у початкову точку (протилежне першому перекладу). Ці 3 афінні перетворення можна об’єднати в одну матрицю, таким чином дозволяючи обертання навколо будь-якої точки зображення.

Усунення шуму зображення за допомогою морфології.

Математична морфологія підходить для усунення шумів у зображеннях. Структуруючі елементи^[en] важливі в математичній морфології.

Наступні приклади стосуються елементів структурування. Функція усунення шумів, зображення як I та структурний елемент як B показані нижче та в таблиці.

e.g. ${\displaystyle (I')={\begin{bmatrix}45&50&65\\40&60&55\\25&15&5\end{bmatrix}}B={\begin{bmatrix}1&2&1\\2&1&1\\1&0&3\end{bmatrix}}}$

Define Dilation(I, B)(i,j) = ${\displaystyle max\{I(i+m,j+n)+B(m,n)\}}$. Let Dilation(I,B) = D(I,B)

D(I', B)(1,1) = ${\displaystyle max(45+1,50+2,65+1,40+2,60+1,55+1,25+1,15+0,5+3)=66}$

Define Erosion(I, B)(i,j) = ${\displaystyle min\{I(i+m,j+n)-B(m,n)\}}$. Let Erosion(I,B) = E(I,B)

E(I', B)(1,1) = ${\displaystyle min(45-1,50-2,65-1,40-2,60-1,55-1,25-1,15-0,5-3)=2}$

After dilation ${\displaystyle (I')={\begin{bmatrix}45&50&65\\40&66&55\\25&15&5\end{bmatrix}}}$ After erosion ${\displaystyle (I')={\begin{bmatrix}45&50&65\\40&2&55\\25&15&5\end{bmatrix}}}$

An opening method is just simply erosion first, and then dilation while the closing method is vice versa. In reality, the D(I,B) and E(I,B) can implemented by Convolution

Structuring element	Mask	Code	Example
Original Image	None	Use Matlab to read Original image original = imread('scene.jpg'); image = rgb2gray(original); [r, c, channel] = size(image); se = logical([1 1 1 ; 1 1 1 ; 1 1 1]); [p, q] = size(se); halfH = floor(p/2); halfW = floor(q/2); time = 3; % denoising 3 times with all method
Dilation	${\displaystyle {\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}}}$	Use Matlab to dilation imwrite(image, "scene_dil.jpg") extractmax = zeros(size(image), class(image)); for i = 1 : time dil_image = imread('scene_dil.jpg'); for col = (halfW + 1): (c - halfW) for row = (halfH + 1) : (r - halfH) dpointD = row - halfH; dpointU = row + halfH; dpointL = col - halfW; dpointR = col + halfW; dneighbor = dil_image(dpointD:dpointU, dpointL:dpointR); filter = dneighbor(se); extractmax(row, col) = max(filter); end end imwrite(extractmax, "scene_dil.jpg"); end
Erosion	${\displaystyle {\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}}}$	Use Matlab to erosion imwrite(image, 'scene_ero.jpg'); extractmin = zeros(size(image), class(image)); for i = 1: time ero_image = imread('scene_ero.jpg'); for col = (halfW + 1): (c - halfW) for row = (halfH +1): (r -halfH) pointDown = row-halfH; pointUp = row+halfH; pointLeft = col-halfW; pointRight = col+halfW; neighbor = ero_image(pointDown:pointUp,pointLeft:pointRight); filter = neighbor(se); extractmin(row, col) = min(filter); end end imwrite(extractmin, "scene_ero.jpg"); end
Opening	${\displaystyle {\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}}}$	Use Matlab to Opening imwrite(extractmin, "scene_opening.jpg") extractopen = zeros(size(image), class(image)); for i = 1 : time dil_image = imread('scene_opening.jpg'); for col = (halfW + 1): (c - halfW) for row = (halfH + 1) : (r - halfH) dpointD = row - halfH; dpointU = row + halfH; dpointL = col - halfW; dpointR = col + halfW; dneighbor = dil_image(dpointD:dpointU, dpointL:dpointR); filter = dneighbor(se); extractopen(row, col) = max(filter); end end imwrite(extractopen, "scene_opening.jpg"); end
Closing	${\displaystyle {\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}}}$	Use Matlab to Closing imwrite(extractmax, "scene_closing.jpg") extractclose = zeros(size(image), class(image)); for i = 1 : time ero_image = imread('scene_closing.jpg'); for col = (halfW + 1): (c - halfW) for row = (halfH + 1) : (r - halfH) dpointD = row - halfH; dpointU = row + halfH; dpointL = col - halfW; dpointR = col + halfW; dneighbor = ero_image(dpointD:dpointU, dpointL:dpointR); filter = dneighbor(se); extractclose(row, col) = min(filter); end end imwrite(extractclose, "scene_closing.jpg"); end

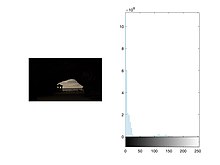
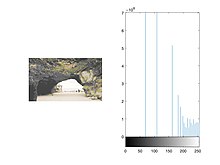
Зображення цифрової камери

Цифрові фотоапарати, як правило, включають спеціалізоване обладнання для обробки цифрових зображень – або спеціальні мікросхеми, або додані схеми на інших мікросхемах – для перетворення необроблених даних із датчика зображення на зображення з корекцією кольорів у стандартному форматі файлу зображення. Додаткові методи пост-обробки підвищують різкість країв або насиченість кольорів для створення більш природних зображень.

Плівка

«Світ заходу» (1973) був першим повнометражним фільмом, який використовував цифрову обробку зображень для піксельної фотографії для імітації точки зору андроїда.[28] Обробка зображень також широко використовується для створення ефекту кольоровості, який замінює фон акторів природним або художнім пейзажем.

Розпізнавання обличчя

Процес виявлення обличчя. Розпізнавання обличчя можна реалізувати за допомогою математичної морфології, дискретного косинусного перетворення, яке зазвичай називають DCT, і горизонтальної проекції (математики).

Загальний метод з методом на основі ознак

Метод визначення обличчя на основі ознак використовує тон шкіри, розпізнавання країв, форму обличчя та особливості обличчя (наприклад, очі, рот тощо) для виявлення обличчя. Тон шкіри, форма обличчя та всі унікальні елементи, які є тільки в людському обличчі, можна описати як особливості.

На якість зображення можуть впливати вібрація камери, надмірна експозиція, занадто централізований розподіл рівнів сірого, шум тощо. Наприклад, проблему шуму можна вирішити за допомогою методу згладжування, тоді як проблему розподілу рівнів сірого можна покращити шляхом вирівнювання гістограми.

Метод згладжування

У малюнку, якщо є якийсь незадоволений колір, беремо деякий колір навколо незадоволеного кольору та усереднюємо їх. Це простий спосіб подумати про метод згладжування.

Метод згладжування можна реалізувати за допомогою маски та згортки. Візьміть, наприклад, маленьке зображення та маску, як показано нижче.

image is ${\displaystyle {\begin{bmatrix}2&5&6&5\\3&1&4&6\\1&28&30&2\\7&3&2&2\end{bmatrix}}}$

mask is ${\displaystyle {\begin{bmatrix}1/9&1/9&1/9\\1/9&1/9&1/9\\1/9&1/9&1/9\end{bmatrix}}}$

After Convolution and smoothing, image is ${\displaystyle {\begin{bmatrix}2&5&6&5\\3&9&10&6\\1&9&9&2\\7&3&2&2\end{bmatrix}}}$

Oberseving image[1, 1], image[1, 2], image[2, 1], and image[2, 2].

The original image pixel is 1, 4, 28, 30. After smoothing mask, the pixel becomes 9, 10, 9, 9 respectively.

new image[1, 1] = ${\displaystyle {\tfrac {1}{9}}}$ * (image[0,0]+image[0,1]+image[0,2]+image[1,0]+image[1,1]+image[1,2]+image[2,0]+image[2,1]+image[2,2])

new image[1, 1] = floor(${\displaystyle {\tfrac {1}{9}}}$ * (2+5+6+3+1+4+1+28+30)) = 9

new image[1, 2] = floor({${\displaystyle {\tfrac {1}{9}}}$ * (5+6+5+1+4+6+28+30+2)) = 10

new image[2, 1] = floor(${\displaystyle {\tfrac {1}{9}}}$ * (3+1+4+1+28+30+7+3+2)) = 9

new image[2, 2] = floor(${\displaystyle {\tfrac {1}{9}}}$ * (1+4+6+28+30+2+3+2+2)) = 9

Gray Level Histogram method

Generally, given a gray level histogram from an image as below. Changing the histogram to uniform distribution from an image is usually what we called Histogram equalization.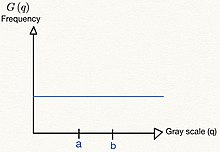

In discrete time, the area of gray level histogram is ${\displaystyle \sum _{i=0}^{k}H(p_{i})}$(see figure 1) while the area of uniform distribution is ${\displaystyle \sum _{i=0}^{k}G(q_{i})}$(see figure 2). It is clear that the area will not change, so ${\displaystyle \sum _{i=0}^{k}H(p_{i})=\sum _{i=0}^{k}G(q_{i})}$.

From the uniform distribution, the probability of ${\displaystyle q_{i}}$ is ${\displaystyle {\tfrac {N^{2}}{q_{k}-q_{0}}}}$ while the ${\displaystyle 0<i<k}$

In continuous time, the equation is ${\displaystyle \displaystyle \int _{q_{0}}^{q}{\tfrac {N^{2}}{q_{k}-q_{0}}}ds=\displaystyle \int _{p_{0}}^{p}H(s)ds}$.

Moreover, based on the definition of a function, the Gray level histogram method is like finding a function ${\displaystyle f}$ that satisfies f(p)=q.

Improvement method	Issue	Before improvement	Process	After improvement
Smoothing method	noise with Matlab, salt & pepper with 0.01 parameter is added to the original image in order to create a noisy image.		read image and convert image into grayscale convolution the graysale image with the mask ${\displaystyle {\begin{bmatrix}1/9&1/9&1/9\\1/9&1/9&1/9\\1/9&1/9&1/9\end{bmatrix}}}$ denoisy image will be the result of step 2.
Histogram Equalization	Gray level distribution too centralized		Refer to the Histogram equalization

• Розпізнавання тексту
• Обробка супутникових знімків
• Машинний зір
• Обробка даних для виділення різних характеристик
• Обробка зображень у медицині
• Ідентифікація особи (по обличчю, райдужці, дактилоскопічним даними)
• Автоматичне управління автомобілями
• Визначення форми об'єкта
• Визначення переміщення об'єкта
• Накладення фільтрів

• Відео
• Редагування зображень
• Апскейлінг

• Нейроподібні методи, алгоритми та структури обробки зображень у реальному часі: монографія / Ю. М. Рашкевич, Р. О. Ткаченко, І. Г. Цмоць, Д. Д. Пелешко ; М-во освіти і науки України, Нац. ун-т «Львів. політехніка». — Львів: Вид-во Львів. політехніки, 2014. — 256 с. : іл. — Бібліогр.: с. 243—252 (166 назв). — ISBN 978-617-607-603-2

Це незавершена стаття з технології. Ви можете допомогти проєкту, виправивши або дописавши її.

Ця стаття не містить посилань на джерела. Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути піддано сумніву та вилучено. (жовтень 2015)