半精度浮動小数点数

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方） 出典検索?: "半精度浮動小数点数" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2019年4月)

半精度浮動小数点数（はんせいどふどうしょうすうてんすう、英: half-precision floating point number）は浮動小数点方式で表現された数（浮動小数点数）の一種で、16ビット（2オクテット）の形式によりコンピュータ上で表現可能な浮動小数点数である。

IEEE 754-2008ではbinary16と名づけられている他、処理系や文脈によってs10e5やhalf、fp16などと表記される。

FP16は当初、主にコンピュータグラフィックス用として提唱された、浮動小数点数フォーマットのひとつである^[1]。

GPUにおいては、リアルタイム3次元コンピュータグラフィックス処理において単精度浮動小数点数に対するスループット向上などを目的に、DirectX 9.0 (Direct3D 9.0) APIとCg/HLSL（シェーディング言語）で利用可能なデータ形式として、NVIDIAとマイクロソフトが共同で策定し、GeForce FXやQuadro FXで採用したのが始まりである。ただし当時のFP16の主な目的は浮動小数テクスチャのデータ量を削減するためのフォーマットであり、FP16のハードウェアアクセラレーションをサポートしないハードウェアにおけるhalf型の演算はfloat型と同じく32ビットの単精度浮動小数点数用の演算器を利用して実行されていたため、演算の速度性能自体には寄与しなかった^[2]。

インダストリアル・ライト&マジック社の研究の中で、広いダイナミックレンジと浮動小数点数の特徴を生かして光量の調整に向いていることが分かり、OpenEXRで採用された。

その後、IEEE 754rを経てIEEE 754-2008でbinary16として、データ交換とデータ容量削減を主目的とした保存用フォーマットとして採用された。

近年^[いつ?]では、ハードウェアサポート（SIMD: Packed FP16）があれば高い演算性能 (FLOPS) が見込める上に、メモリ容量やディスク容量が節約できることから、ディープラーニングにおいて利用が活発化している。

誕生の経緯から、リアルタイムグラフィックス用途で利用されているほか、HDRレンダリング (High-Dynamic-Range Rendering) などプロダクション用途で利用が可能である。ダイナミックレンジを広くとることができることから、アニメーションやCGなどの用途で利用されることが多いが、一般的な画像ファイルフォーマットとして対応しているものは少なく、OpenEXRやDDSといった特殊な形式に限られる。

また、ハードウェアの支援があればスループットが劇的に向上し、かつ、nビットの乗算器の回路規模はn²log(n)に比例するので、仮数部11ビットの半精度浮動小数点数の乗算器の規模、すなわちチップに占める面積は、16ビットの整数乗算器の半分程度であり（ただし加減算に必要な、正規化のためのシフト処理は別途必要）、同一面積のチップに実装できる積和演算器の数も大幅に増やすことができる。モバイル向けGPUでは消費電力と性能と精度のバランスの観点から、既定でFP32よりもFP16が使われることが多い。重み付け係数を格納するストレージ容量の節約になることも相まって、並列度の高いディープラーニング用途において注目が集まっており、パーソナルコンピュータ／ワークステーション／サーバー向けにおいても対応GPUが増加し、FPGAでの実装や汎用的な信号処理用のアクセラレータの研究も進んでいる。

IEEE 754標準はbinary16を以下のように定めている。

• 符号ビット: 1 ビット
• 指数部の幅: 5 ビット
• 仮数部の幅＝精度: 11 (明示的には10ビット)

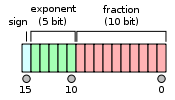
他のIEEE754浮動小数点表現と同様、指数部が全0でない限り黙示的な「1」のビットを仮数部に持つ（いわゆる「ケチ表現」）。このため仮数部に記録するのは10ビットだが11ビットの精度を持つ。${\displaystyle \log _{10}(2^{11})\approx 3.311}$より、これは十進数にしておよそ3桁の値となる。ビットは下図のように並ぶ。

半精度2進浮動小数点数の指数部はオフセット2進表現でエンコードされており、オフセット（IEEE 754における指数部バイアス）は15である。

• E_min = 0x01−0x0f = −14
• E_max = 0x1e−0x0f = 15
• 指数部バイアス = 0x0f = 15

よって、真の指数を得るためには、記録された指数から15を引けばよい。

記録された指数の0x00と0x1fは特別に扱われる。

指数	仮数=0	仮数≠0	式
0x00	0, −0	非正規化数	${\displaystyle (-1)^{\text{signbit}}\times 2^{-14}\times 0.{\text{significandbits}}_{2}}$
0x01, ..., 0x1e	正規化数		${\displaystyle (-1)^{\text{signbit}}\times 2^{{{\text{exponentbits}}_{2}}-15}\times 1.{\text{significandbits}}_{2}}$
0x1f	±無限大	NaN (quiet, signalling)

• 最小の正の非正規化数 : 2⁻²⁴ ≈ 5.96 × 10⁻⁸
• 最小の正の正規化数 : 2⁻¹⁴ ≈ 6.10 × 10⁻⁵
• 表現可能な最大数 : 65504

浮動小数点数値のビット列を十六進法で表した例を以下に示す。これには符号、オフセットを加えた指数値、仮数値が含まれている。

3c00   = 1
3c01   = 1.0009765625、1より大きい最小の数
3c02   = 1.001953125
3fff   = 1.9990234375、2より小さい最大の数
4000   = 2
c000   = -2

7bfe   = 65472
7bff   = 65504  （半精度数の正の最大値。符号なし16ビット整数の最大数(65535)と大差ない）
fbff   = -65504  （半精度数の負の最大値）

0400   = 2-14 ≈ 6.10352 × 10-5 （最小の正の正規化数）

0001   = 2-24 ≈ 5.96046 × 10-8 （最小の正の非正規化数）

0000   = 0
8000   = -0

7c00   = 正の無限大
fc00   = 負の無限大

3555   ≈ 0.33325... ≈ 1/3

1/3は切り下げられる。これは仮数部のビット数が奇数であるため（1/3は2進小数で0.01010101...）である。

この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方） 出典検索?: "半精度浮動小数点数" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2019年4月)

• NVIDIA: Pascalアーキテクチャ以降のGeForce/Quadro/Teslaシリーズ^{[3][注釈 1]}、またMaxwellアーキテクチャ以降のTegraシリーズにてPacked FP16をサポート^[4]。
• ARM VFPv3のオプションとしてfp16が利用可能。
• AMD: AMD Radeon RX Vegaシリーズにてサポート。Radeonとしては初めてbinary16の並列処理が可能になる。

• OpenCL - OpenCL 1.0の拡張として、cl_khr_fp16が有効であれば利用可能。
• OpenCV - 3.3.0以降でfloatとhalfの変換が利用可能。
• Cg - 組み込みのhalf型として実装されている。
• CUDA - half型を直接扱う演算子のサポートはないが、float型などとの相互変換関数^[5]や各種演算用の組み込み関数^[6]が用意されている。
• Direct3D/HLSL - Direct3D 9以降のテクスチャフォーマットとしてFP16をサポート。また、Direct3D 9以降のHLSLでhalf型をサポート。Direct3D 10ではhalfは常にfloatとして扱われる^[7]。DirectX 11.1 (Direct3D 11.1) 以降では低精度シェーダー（最低精度シェーダー）をサポートし^[8]、min16floatとして対応ハードウェア上で利用できるが、この低精度シェーダー機能はMicrosoft Windows 8以降でしか動作しない^[9]。
• OpenGL/OpenGL ES/GLSL - OpenGL 3.0以降のテクスチャフォーマットとしてFP16をサポート^[10]。GLSLではmediumpとして利用可能。
• C++ - s10e5として実装例^{[要出典][要説明]}がある。
• OpenEXR - C++向けのhalfクラス型が提供されている^[11]。
• macOSではMac OS X v10.4以降にて、RGBA各チャンネルが16ビット浮動小数点数（ピクセルあたり64ビット）のピクセルフォーマットkCIFormatRGBAhがサポートされている^[12]。

1. ^ 3Dグラフィックス・マニアックス(42) HDRレンダリング(2)～HDRレンダリングの第一の効能 | マイナビニュース
2. ^ GeForce FXシリーズのパフォーマンスの核心に迫る
3. ^ 【後藤弘茂のWeekly海外ニュース】倍精度浮動小数点演算性能を引き上げた新GPUアーキテクチャ「Pascal」 - PC Watch
4. ^ 【後藤弘茂のWeekly海外ニュース】1TFLOPSのNVIDIAモバイルSoC「Tegra X1」 - PC Watch
5. ^ CUDA Math API :: CUDA Toolkit Documentation
6. ^ Mixed-Precision Programming with CUDA 8 | NVIDIA Developer Blog
7. ^ Scalar Types - Windows applications | Microsoft Docs
8. ^ 【GDC2012】西川善司の3Dゲームファンのための「DirectX 11.1」講座 - GAME Watch
9. ^ Using HLSL minimum precision - Windows applications | Microsoft Docs
10. ^ glTexImage2D - OpenGL 4 Reference Pages
11. ^ openexr/half.h at master · AcademySoftwareFoundation/openexr
12. ^ kCIFormatRGBAh - Core Image | Apple Developer Documentation

• Minifloats (Survey of Floating-Point Formatsの中)
• OpenEXR site
• OpenGL treatment of half precision
• ^[リンク切れ] Analog devices variant (4ビット指数)
• C source code to convert between IEEE double, single, and half precision can be found here
• Half-precision floating point in C# C#で書かれたフリーのhalf floatライブラリ