|
Géométrie descriptiveExemples de longueurs et d’angles en vraie grandeur dans certaines projections, choisies à cet effet. Ici un cube et un dodécaèdre de Platon, de même sphère circonscrite, ont toutes leurs arêtes de longueur a ou d = φ a La géométrie descriptive fut inventée par le mathématicien français Gaspard Monge. C'est une branche de la géométrie qui définit les méthodes nécessaires à la résolution graphique des problèmes d'intersections et d'ombres entre volumes et surfaces définis de façon géométrique dans l'espace à trois dimensions. Il s'agit, en général, de rechercher la vraie grandeur de cotes, de tracer les courbes d'intersections de solides, de déterminer la nature de courbes (ellipse, parabole, hyperbole), de développer des surfaces (conique, cylindrique, prismatique…) ou encore de dessiner un objet selon un angle de vision donné (rotation, rabattement, changement de plan dans l'espace). UtilitéCes problèmes sont pour une part ceux qui étaient posés dans les métiers de la taille des pierres de la charpente (exemple des escaliers débillardés, etc.), de l'usinage et, plus généralement, des métiers mettant en œuvre les métaux en feuille (tôlerie, carrosserie, dinanderie, chaudronnerie). Notons que dans ce dernier cas, l'application spécifique des principes de la géométrie descriptive prend le nom de « traçage des métaux en feuille » (ou simplement « traçage »). La géométrie descriptive a été théorisée par le mathématicien français Gaspard Monge (1746-1818), mais les méthodes de projection lui étaient antérieures. Elle consiste donc à représenter un ou plusieurs objets de l'espace à 3 dimensions en un minimum de projections orthogonales pour en lever l'ambiguïté et conserver, pour le problème posé, le maximum de propriétés utiles (conservation d'angles et de longueurs). Les projections sont toutes orthogonales. Leurs plans sont choisis en fonction de l’objet à décrire, ou du problème posé. Par exemple une projection qui ne déforme pas certains angles peut être intéressante. Souvent deux projections suffisent, leur nombre dépasse rarement trois. Les conventions suivantes facilitent la lecture d’une figure en géométrie descriptive.
Le « dessin géométral », couramment appelé dessin industriel, met aussi en œuvre la géométrie descriptive, avec des conventions un peu différentes. Représentation des points d'intersection d'une droite quelconque avec un cône oblique à base elliptiqueÉpure réalisée au moyen de deux vues, une vue frontale et une vue horizontale, ces deux vues étant séparées par une ligne de terre (LT), les points d'intersection sont représentés en {G,H}. 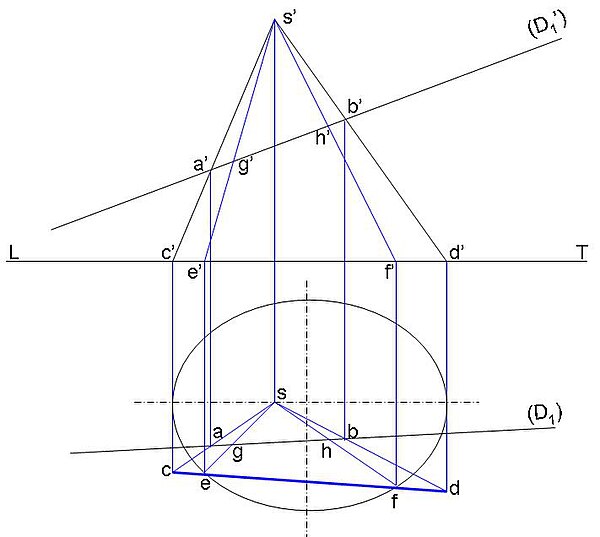 Explication de l'épure au moyen d'une représentation en perspective :  Représentation d'une intersection entre deux volumes L'intersection de deux volumes (par exemple un perçage débouchant en surface ou bien deux pièces soudées) suit souvent une courbe « complexe ». Le dessin de cette courbe nécessite de repérer les points sur deux projections : le point appartient aux deux volumes, une des vues va donner sa cote, l'autre vue son éloignement. La construction de cette courbe va se faire « point par point », avec la méthode du plan auxiliaire. Voir aussiArticles connexes
Liens externes
|

