Distancia focal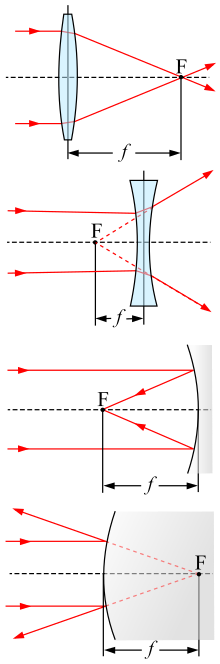

La distancia focal o longitud focal de un lente es la distancia entre el centro óptico de la lente y el foco (o punto focal). La inversa de la distancia focal de una lente es la potencia, y se mide en dioptrías.^[1]​

Para una lente positiva (convergente), la distancia focal es positiva. Se define como la distancia desde el centro óptico de la lente (lugar por donde los rayos incidentes no son desviados) hasta el lugar donde un haz de luz de rayos paralelos al eje óptico que atraviesa la lente se enfoca, llamado foco. Para una lente negativa (divergente), la distancia focal es negativa. Se define como la distancia que hay desde el centro óptico de la lente a un punto imaginario del cual parece emerger el haz de luz que pasa a través de ella.^[1]​

Para un espejo con curvatura esférica, la distancia focal es igual a la mitad del radio de curvatura del espejo. La distancia focal es positiva para un espejo cóncavo, y negativa para un espejo convexo. En la convención de signos utilizada en el diseño óptico, un espejo cóncavo tiene un radio de curvatura negativo.^[2]​

Para un lente delgado que se encuentra en el aire, la distancia focal es la distancia desde el centro de la lente hasta cualquiera de los principales focos (o puntos focales) del lente. Para un lente convergente (por ejemplo, un lente convexo), la longitud focal es positiva, y es la distancia a la que se enfocará un haz de luz colimada a un solo punto. Para un lente divergente (por ejemplo, un lente cóncava), la longitud focal es negativa, y es la distancia hasta el punto sobre el que aparece un haz colimado para ser divergido tras decir pasar a través del lente.^[1]​

Cuando se usa un lente para formar una imagen de un objeto, la distancia del objeto al lente u, la distancia del lente a la imagen v, y la longitud focal f están relacionados por^[2]​

${\displaystyle {\frac {1}{f}}={\frac {1}{u}}+{\frac {1}{v}}}$.

La longitud focal de un lente delgado se puede medir fácilmente mediante el uso del lente para formar una imagen de una fuente de luz distante en una pantalla. El lente es movido hasta que una imagen nítida se forme sobre la pantalla. En este caso 1 / u es despreciable, y la longitud focal entonces viene dada por^[2]​:

${\displaystyle f\approx v}$.

También es posible calcular la distancia focal de una lente generando una imagen de un objeto que tenga el mismo tamaño (escala 1:1). Para ello tanto el objeto como la imagen estarán al doble de la distancia focal. Y por tanto la distancia entre el objeto y la imagen producida al mismo tamaño será cuatro veces la distancia focal.

Para lentes gruesas (que tengan un espesor no despreciable), o un sistema de imagen que consta de varias lentes o espejos (por ejemplo, una lente fotográfica o un telescopio), la longitud focal a menudo se llama la distancia focal efectiva (EFL), para distinguirlo de otros parámetros utilizados comúnmente:

Diagrama de lentes gruesas

• Longitud focal frontal (FFL) o la distancia focal frontal (FFD) (SF) es la distancia desde el punto focal frontal del sistema (F) hasta el vértice de la primera superficie óptica (S1).

• Longitud focal de última (BFL) o la distancia focal posterior (BFD) (s'F ') es la distancia desde el vértice de la última superficie óptica del sistema (S2) hasta el punto focal posterior (F').

Para un sistema óptico en el aire, la longitud focal efectiva (F y F') da la distancia de delante y detrás de los planes principales (H y H') hasta los centros de coordinación correspondientes (F y F'). Si el medio circundante no es aire, entonces la distancia se multiplica por el índice de refracción del medio (n es el índice de refracción de la sustancia de la que está hecha la lente en sí; n1 es el índice de refracción de cualquier medio delante de la lente; n2 es el de cualquier tipo de soporte en la parte posterior de la misma). Algunos autores denominan estas distancias como distancias focales delanteras/traseras, distinguiéndolas de las distancias focales delanteras/traseras que se han definido anteriormente^[2]​.

En general, la longitud focal o EFL es el valor que describe la capacidad del sistema óptico para enfocar la luz, y es el valor que se utiliza para calcular la ampliación del sistema. Los otros parámetros se utilizan en la determinación en la que se formará una imagen de una posición de objeto dada.

Para el caso de una lente de espesor d en el aire (n1 = n2 = 1), y superficies con radios de curvatura R1 y R2, la distancia focal efectiva f se da por la ecuación del fabricante de lentes:

${\displaystyle {\frac {1}{f}}=(n-1){\biggl (}{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n+1)d}{nR_{1}R_{2}}}{\biggr )}}$,

donde n es el índice de refracción del medio de la lente. La cantidad 1/f también se conoce como la potencia óptica de la lente.

La distancia focal frontal correspondiente es^[2]​:

${\displaystyle FFD=P{\biggl (}1+{\frac {(n-1)d}{nR_{2}}}{\biggr )}}$,

y la distancia focal posterior:

${\displaystyle BFD=f{\biggl (}1-{\frac {(n-1)d}{nR_{1}}}{\biggr )}}$,

En la convención de signos utilizada aquí, el valor de R1 será positivo si la primera superficie de la lente es convexa, y negativo si es cóncava. El valor de R2 es negativo si la segunda superficie es convexa y positiva si cóncava. Recuerde que las convenciones de signos varían entre los diferentes autores, lo que resulta en diferentes formas de estas ecuaciones en función de la convención utilizada.

Para un espejo esférico curvado en el aire, la magnitud de la distancia focal es igual al radio de curvatura del espejo dividido por dos. La distancia focal es positiva para un espejo cóncavo, y negativo para un espejo convexo. En la convención de signos utilizados en el diseño óptico, un espejo cóncavo tiene un radio de curvatura negativo, así^[2]​

${\displaystyle f=-{\frac {R}{2}}}$,

donde R es el radio de curvatura de la superficie del espejo.

Objetivo de 28 mm

Objetivo de 50 mm

Objetivo de 70 mm

Objetivo de 210 mm

Un ejemplo de cómo la elección del objetivo afecta al ángulo de visión. Las fotos de arriba se tomaron con una cámara de 35 mm a una distancia fija del sujeto.

Las distancias focales de las lentes de cámara generalmente se indican en milímetros (mm), aunque algunas lentes están identificadas en centímetros (cm) o pulgadas.

La distancia focal (f) y el campo de visión (FOV) de una lente son inversamente proporcionales. Para una lente rectilínea estándar, FOV = 2 arctan x/2f, donde x es la diagonal de la película.

Cuando una lente fotográfica se configura en "infinito", su plano principal posterior se separa del sensor o la película, que se sitúa en el plano focal, gracias a la distancia focal de la lente. Los objetos lejos de la cámara producen imágenes nítidas en el sensor o la película, que también se encuentra en el plano de la imagen.

Para enfocar nítidamente objetos más cercanos, el objetivo debe ajustarse para aumentar la distancia entre el plano principal posterior y la película, para situar la película en el plano de la imagen. La distancia focal (f), la distancia entre el plano principal delantero y el objeto a fotografiar (s₁), y la distancia desde el plano principal posterior hasta el plano de la imagen (s₂) se relacionan mediante la expresión:

${\displaystyle {\frac {1}{s_{1}}}+{\frac {1}{s_{2}}}={\frac {1}{f}}.}$

Al disminuir s₁, s₂ se debe aumentar. Por ejemplo, para una lente normal para una cámara formato de 35mm con una distancia focal f = 50 mm. Para enfocar un objeto distante (s₁ ≈ ∞), el plano principal posterior de la lente debe estar ubicado a una distancia s₂ = 50 mm del plano de la película, de forma tal que se encuentre ubicado en la posición del plano de la imagen. Para enfocar un objeto que se encuentra a 1 m de distancia (s₁ = 1,000 mm), la lente se debe desplazar 2.6 mm alejándose del plano de la película, hasta s₂ = 52.6 mm.

.

La distancia focal de una lente determina el aumento con el que toma imágenes de objetos distantes. Es igual a la distancia entre el plano de la imagen y una agujero que toma imágenes de objetos distantes del mismo tamaño que la lente en cuestión. Para lentes rectilíneos (es decir, sin distorsión de imagen), la imagen de objetos distantes está bien modelada como un modelo de cámara estenopeica.^[3]​ Este modelo conduce al modelo geométrico simple que utilizan los fotógrafos para calcular el ángulo de visión de una cámara; en este caso, el ángulo de visión depende sólo de la relación entre la distancia focal y el tamaño de la película. En general, el ángulo de visión depende también de la distorsión.^[4]​

Un objetivo con una distancia focal aproximadamente igual a la diagonal del formato de la película o del sensor se conoce como objetivo normal; su ángulo de visión es similar al ángulo subtendido por una impresión lo suficientemente grande vista a una distancia de visión típica de la diagonal de impresión, lo que, por tanto, produce una perspectiva normal al ver la impresión;^[5]​ este ángulo de visión es de unos 53 grados en diagonal. Para las cámaras de formato completo de 35 mm, la diagonal es de 43 mm y un objetivo "normal" típico tiene una distancia focal de 50 mm. Un objetivo con una distancia focal inferior a la normal suele denominarse objetivo gran angular (normalmente 35 mm o menos, para cámaras de formato de 35 mm), mientras que un objetivo significativamente más largo de lo normal puede denominarse teleobjetivo (normalmente 85 mm o más, para cámaras de formato de 35 mm). Técnicamente, los objetivos de distancia focal larga sólo son "teleobjetivos" si la distancia focal es mayor que la longitud física del objetivo, pero el término se utiliza a menudo para describir cualquier objetivo de distancia focal larga.

Debido a la popularidad de la película de 135 (35 mm estándar), las combinaciones de cámara y objetivo suelen describirse en términos de su distancia focal equivalente a 35 mm, es decir, la distancia focal de un objetivo que tendría el mismo ángulo de visión, o campo de visión, si se utilizara en una cámara réflex digital de fotograma completo de 35 mm. El uso de una distancia focal equivalente a 35 mm es especialmente común en las cámaras digitales, que suelen utilizar sensores más pequeños que los de las películas de 35 mm, por lo que necesitan distancias focales más cortas para conseguir un ángulo de visión determinado, en un factor conocido como factor de recorte.

La distancia focal de un sistema permite determinar su convergencia o divergencia. La vergencia se mide en dioptrías, denotada δ, y equivalente al recíproco del metro (m⁻¹). La convergencia se calcula de la siguiente forma:^[6]​

${\displaystyle V={\frac {(-1)^{m}n'}{f\,'}}}$.

${\displaystyle n'}$ es el índice de refracción del medio de salida, y ${\displaystyle f\,'}$ la distancia focal de la imagen del sistema. ${\displaystyle m}$ corresponde al número de elementos catótricos, espejos y superficies reflectantes, del sistema. ${\displaystyle V}$ por tanto es negativo para un sistema divergente, positivo para un sistema convergente, cuando el eje óptico está orientado en la dirección de propagación de la luz.^[7]​

Todos los métodos para determinar la distancia focal de los sistemas ópticos pertenecen a un campo de la metrología óptica llamado focometría.

• Autocolimación es un método experimental para determinar las distancias focales de sistemas convergentes. Una fuente se coloca delante del sistema y un espejo en la parte trasera del sistema. El método consiste en ajustar la distancia de la fuente, hasta que su imagen por el conjunto del sistema espejo se superpone a la fuente.^[8]​

• El método de Silbermann: cuando la lenta se coloca de tal modo que la imagen en una pantalla (imagen real) tenga el mismo tamaño que el objeto entonces la distancia entre la imagen y el objeto son cuatro veces la distancia focal.^[9]​

• El método Badal permite medir la distancia focal de lentes divergentes.
• El método Bessel es adecuado para lentes convergentes.^[10]​

La potencia óptica de una lente o de un espejo curvado es una magnitud física igual a la recíproca de la distancia focal, expresado en metros. Una dioptría es su unidad de medida con dimensión de longitud recíproca, equivalente a un metro recíproco, 1 dioptría = 1 m⁻¹. Por ejemplo, una lente de 2 dioptros aporta rayos paralelos de luz para enfocar ¹⁄₂ metro. Una ventana plana tiene una potencia óptica de cero dioptrías, puesto que no hace que la luz converge ni diverge.^[11]​

La principal ventaja de utilizar la potencia óptica en lugar de la distancia focal es que la fórmula de la lente fina tiene la distancia del objeto, la distancia de la imagen y la distancia focal como recíprocos. Además, cuando las lentes finas relativamente delgadas se colocan juntas, sus potencias se suman aproximadamente. Así, una lente delgada de 2,0 dioptrías colocada cerca de una lente delgada de 0,5 dioptrías produce casi la misma distancia focal que una única lente de 2,5 dioptrías.

Debido al uso extensivo, estas lentes tienen características de diferentes distancias focales, pero no necesariamente de diferentes tipos, tales como lentes gran angular, normales y tele.

Las lentes 'Zoom' también se dividen en familias, dependiendo de las distancias focales, con algunas de estas lentes que tienen la función macro.

Su producción comenzó en 1959, y en un principio los resultados obtenidos fueron muy poco satisfactorios, lo que hizo que no fuera popular entre los fotógrafos. Hoy en día son muy populares y tienen fama de ofrecer buenas imágenes, siendo utilizados a gran escala por cámaras de pequeño formato. Representan una opción de óptica de excelente calidad y coste económico para el fotógrafo, además de la practicidad que ofrecen.

Los objetivos de distancia focal variable pueden tener su zoom medido por la relación entre su distancia focal máxima y la distancia focal mínima (Z=DFmax/DDmin). Por lo tanto, el zoom no se puede utilizar para definir el ángulo de visión de una lente, ya que la relación puede ser la misma para lentes con diferentes distancias focales.^[12]​ Se pueden ver ejemplos en la siguiente tabla:

* Ángulos de visión calculados para objetos lejanos y para la diagonal de un soporte de formato 135.^[12]​

• Apertura
• Dioptría
• Óptica
• Distancia hiperfocal
• Factor de multiplicación de la distancia focal
• Foco
• Número f
• Objetivo (fotografía)
• Profundidad de campo

• Ejemplos de distancia focal
• Distancia focal en fotografía

• Balland, Bernard (2007). Presses polytechniques et universitaires romandes, ed. Optique géométrique (en francés). Lausanne. p. 860. ISBN 978-2-88074-689-6. 

• Taillet, Richard; Febvre, Pascal; Villain, Loïc (2013). «Dictionnaire de physique». En De Boeck, ed. De Boeck Supérieur (en francés) (3). p. 899.